平行四边形奥赛[下学期]
图片预览


文档简介
平行四边形
知识扩展:
1、利用平行四边形的性质是求边、角关系的常用方法。
2、若凸四边形各边的平方和等于两条对角线的平方和,则此凸四边形是平行四边形,其逆亦成立。
3、过平行四边形对称中心的直线将平行四边形分成两部分,这两部分的面积相等。
4、平行四边形区域上的三角形面积不大于该平行四边形面积的一半。
方法指导:
例1 如图, ABCD中,BE⊥AD,BF⊥CD,△BEF的垂心(三条高的交点)为H,若DG⊥BC,求证:BH=GF。
分析:此题利用平行四边形证边等。
注意寻找关于BH、GF的平行四边形。
例2 如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上且AN=MC,AM与BN相交于P,求证:∠BPM=45°。
分析:此题可构造平行四边形
转化已知相等线段构造特殊三角形。
过M作ME⊥BC,使ME=AN,连结ME、EC。
例3 ABCD中,E、F分别在CD、AD上,AE=CF,AE、CF交于G,连结BG,
求证:BG平分∠AGC。
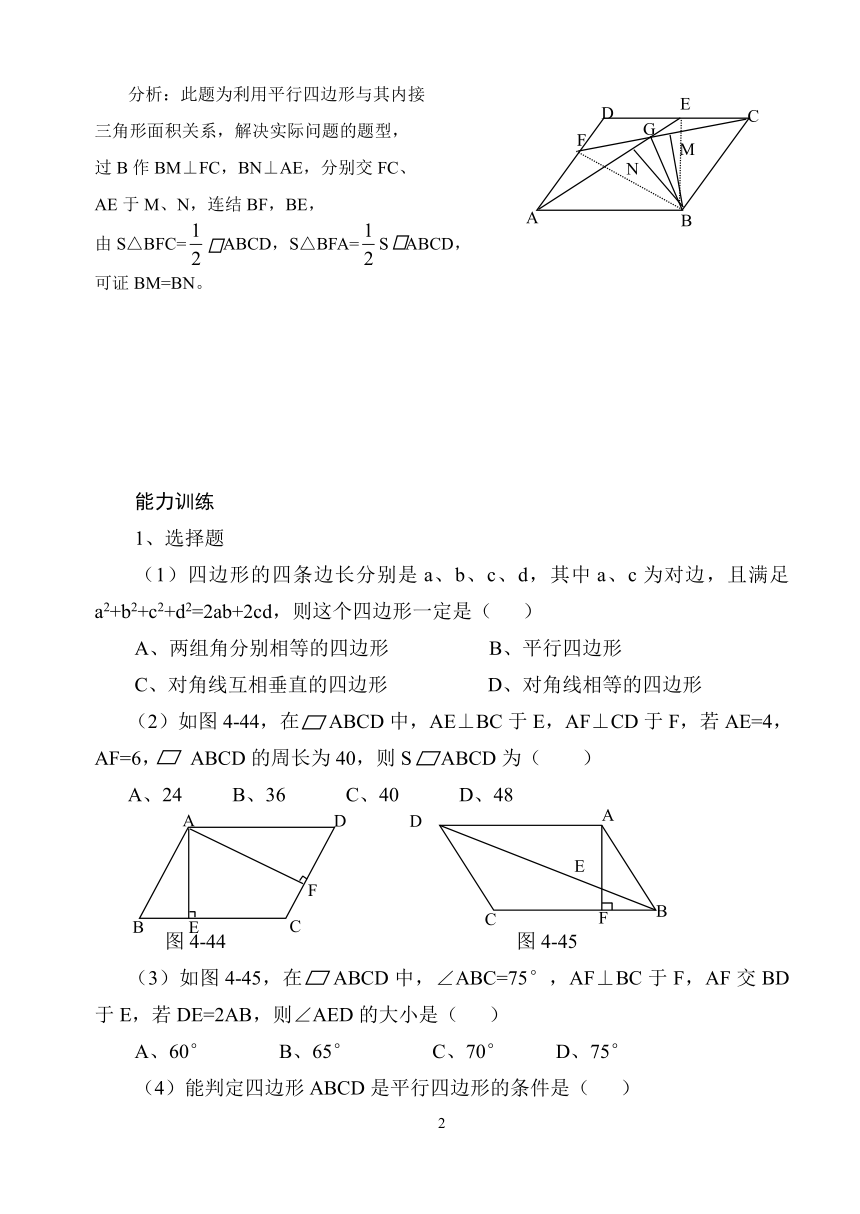
分析:此题为利用平行四边形与其内接
三角形面积关系,解决实际问题的题型,
过B作BM⊥FC,BN⊥AE,分别交FC、
AE于M、N,连结BF,BE,
由S△BFC= ABCD,S△BFA=S ABCD,
可证BM=BN。
能力训练
1、选择题
(1)四边形的四条边长分别是a、b、c、d,其中a、c为对边,且满足a2+b2+c2+d2=2ab+2cd,则这个四边形一定是( )
A、两组角分别相等的四边形 B、平行四边形
C、对角线互相垂直的四边形 D、对角线相等的四边形
(2)如图4-44,在 ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6, ABCD的周长为40,则S ABCD为( )
A、24 B、36 C、40 D、48
图4-44 图4-45
(3)如图4-45,在 ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED的大小是( )
A、60° B、65° C、70° D、75°
(4)能判定四边形ABCD是平行四边形的条件是( )
A、∠A=∠B=∠C B、AB=BC=CD
C、∠A=∠C,AB∥CD D、AB=CD,AD∥BC
(5)从等腰三角形底边上的任意一点作两腰的平行线,所构成的平行四边形的周长等于这个等腰三角形的( )
A、腰长 B、周长的一半 C、腰长的2倍 D、周长
(6)给定平面内不在一直线上的三点,以这三点为顶点的平行四边形有( )
A、1个 B、2个 C、3个 D、4个
(7)根据下列条件,能作出平行四边形的是( )
A、相邻两边的长分别是3和5,且一条对角线的长为9
B、两组对边的长分别是3和5
C、一边的长为7,两条对角线的长分别为6和8
D、一边的长为7,两条对角线的长分别为6和5
(8)在 ABCD中,DE⊥AB,DF⊥BC,垂足分别为E、F,设∠EDF
=60°,则S△DEF:S ABCD=( )
A、 B、 C、 D、
(9)、如图, ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD
于E,若DE=2AB,则∠AED的大小是( )
A、60° B、65° C、70° D、75°
2、填空题
(1)如图4-46, ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,若△CDM的周长为a,那么 ABCD的周长为 。
图4-46 图4-47 图4-48
(2)如图4-47, ABCD中,AB=2,BC=3,∠ABC、∠BCD的平分线分别交AD于E、F,则EF= 。
(3)如图4-48,E在 ABCD对角线AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,则 ABCD的面积是 。
(4)已知 ABCD的周长为52,自顶点D作DE⊥AB,DF⊥BC,E、F为垂足,若DE=5,DF=8,则BE+BF的长为 。
(5)、如图 ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC交AD于点M,若△CDM周长为a,那么 ABCD的周长为 。
(6)、如图,已知ABCD是平行四边形,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,则 ABCD的面积是 。
(5)题 (6)题
3、如图4-49,△ABC是正三角形,在AB、BC边上分别取点E、D,使AE=BD,顶点D、E分别作DF∥CE,EF∥CD,EF交DF于F点,延长FE交AC于G,求证:△AGF≌△EAC。
4、如图4-50,以 ABCD的BC、CD边为边在四边形内侧作等边△BCE和等边△CDF,求证:△AEF为等边三角形。
5、以△ABC的三条边为边向BC的同侧作等边△ABP、等边△ACQ、等边△BCR,求证:四边形PAQR为平行四边形。
6、在 ABCD中,AB=2AD,E为AB的中点,求证:CE⊥DE。
7、如图4-51,在 ABCD中,E、F分别为BC、AB上的点,且AE=CF,AE、CF交于G,求证:GD平分∠AGC。
图4-51 图4-52
8、如图4-52,在△ABC中,∠C=90°,点M在BC上,且BM、AC,点N在AC上,且AN=MC,AM、BN相交于P,求证:∠BPM=45°。
9、已知,如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,E、F为垂足,EM⊥AD,FN⊥BC,M、N为垂足,求证:MF∥EN,MF=EN,
10、如图,在 ABCD中,3AB=2AD,E1、E2、E3、E4、E5依次是CB上的五个点,并且CE1=E1E2=E2E3=E3E4=E4E5=E5B,在三个结论中,(1)BE3⊥AE3,(2)AE2⊥DE4,(3)AE2⊥DE2之中,正确的个数是 。
5题
创新思维
如图,C为线段AB的中点,以AC及BC为对角线作平行四边形ADCE和BFCG,再作平行四边形CDHF及CEKG。
求证:H、C、K三点共线。
B
A
F
D
N
M
E
C
A
B
F
C
G
B
H
E
A
C
E
M
N
E
D
C
B
F
A
B
A
O
C
M
D
E
C
D
A
F
B
A
M
E
B
F
N
C
D
A
D
C
B
E1
E2
E3
E4
E5
C
K
E
A
D
G
B
F
H
B
P
M
C
N
A
D
C
E
B
G
F
A
图4-50
图4-49
B
C
D
E
F
A
B
D
C
F
E
G
A
D
C
E
B
F
A
B
C
D
E
F
A
O
B
C
D
M
A
D
P
G
C
B
E
F
A
D
C
F
B
E
A
D
1
2
知识扩展:
1、利用平行四边形的性质是求边、角关系的常用方法。
2、若凸四边形各边的平方和等于两条对角线的平方和,则此凸四边形是平行四边形,其逆亦成立。
3、过平行四边形对称中心的直线将平行四边形分成两部分,这两部分的面积相等。
4、平行四边形区域上的三角形面积不大于该平行四边形面积的一半。
方法指导:
例1 如图, ABCD中,BE⊥AD,BF⊥CD,△BEF的垂心(三条高的交点)为H,若DG⊥BC,求证:BH=GF。
分析:此题利用平行四边形证边等。
注意寻找关于BH、GF的平行四边形。
例2 如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上且AN=MC,AM与BN相交于P,求证:∠BPM=45°。
分析:此题可构造平行四边形
转化已知相等线段构造特殊三角形。
过M作ME⊥BC,使ME=AN,连结ME、EC。
例3 ABCD中,E、F分别在CD、AD上,AE=CF,AE、CF交于G,连结BG,
求证:BG平分∠AGC。
分析:此题为利用平行四边形与其内接
三角形面积关系,解决实际问题的题型,
过B作BM⊥FC,BN⊥AE,分别交FC、
AE于M、N,连结BF,BE,
由S△BFC= ABCD,S△BFA=S ABCD,
可证BM=BN。
能力训练
1、选择题
(1)四边形的四条边长分别是a、b、c、d,其中a、c为对边,且满足a2+b2+c2+d2=2ab+2cd,则这个四边形一定是( )
A、两组角分别相等的四边形 B、平行四边形
C、对角线互相垂直的四边形 D、对角线相等的四边形
(2)如图4-44,在 ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6, ABCD的周长为40,则S ABCD为( )
A、24 B、36 C、40 D、48
图4-44 图4-45
(3)如图4-45,在 ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED的大小是( )
A、60° B、65° C、70° D、75°
(4)能判定四边形ABCD是平行四边形的条件是( )
A、∠A=∠B=∠C B、AB=BC=CD
C、∠A=∠C,AB∥CD D、AB=CD,AD∥BC
(5)从等腰三角形底边上的任意一点作两腰的平行线,所构成的平行四边形的周长等于这个等腰三角形的( )
A、腰长 B、周长的一半 C、腰长的2倍 D、周长
(6)给定平面内不在一直线上的三点,以这三点为顶点的平行四边形有( )
A、1个 B、2个 C、3个 D、4个
(7)根据下列条件,能作出平行四边形的是( )
A、相邻两边的长分别是3和5,且一条对角线的长为9
B、两组对边的长分别是3和5
C、一边的长为7,两条对角线的长分别为6和8
D、一边的长为7,两条对角线的长分别为6和5
(8)在 ABCD中,DE⊥AB,DF⊥BC,垂足分别为E、F,设∠EDF
=60°,则S△DEF:S ABCD=( )
A、 B、 C、 D、
(9)、如图, ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD
于E,若DE=2AB,则∠AED的大小是( )
A、60° B、65° C、70° D、75°
2、填空题
(1)如图4-46, ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,若△CDM的周长为a,那么 ABCD的周长为 。
图4-46 图4-47 图4-48
(2)如图4-47, ABCD中,AB=2,BC=3,∠ABC、∠BCD的平分线分别交AD于E、F,则EF= 。
(3)如图4-48,E在 ABCD对角线AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,则 ABCD的面积是 。
(4)已知 ABCD的周长为52,自顶点D作DE⊥AB,DF⊥BC,E、F为垂足,若DE=5,DF=8,则BE+BF的长为 。
(5)、如图 ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC交AD于点M,若△CDM周长为a,那么 ABCD的周长为 。
(6)、如图,已知ABCD是平行四边形,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,则 ABCD的面积是 。
(5)题 (6)题
3、如图4-49,△ABC是正三角形,在AB、BC边上分别取点E、D,使AE=BD,顶点D、E分别作DF∥CE,EF∥CD,EF交DF于F点,延长FE交AC于G,求证:△AGF≌△EAC。
4、如图4-50,以 ABCD的BC、CD边为边在四边形内侧作等边△BCE和等边△CDF,求证:△AEF为等边三角形。
5、以△ABC的三条边为边向BC的同侧作等边△ABP、等边△ACQ、等边△BCR,求证:四边形PAQR为平行四边形。
6、在 ABCD中,AB=2AD,E为AB的中点,求证:CE⊥DE。
7、如图4-51,在 ABCD中,E、F分别为BC、AB上的点,且AE=CF,AE、CF交于G,求证:GD平分∠AGC。
图4-51 图4-52
8、如图4-52,在△ABC中,∠C=90°,点M在BC上,且BM、AC,点N在AC上,且AN=MC,AM、BN相交于P,求证:∠BPM=45°。
9、已知,如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,E、F为垂足,EM⊥AD,FN⊥BC,M、N为垂足,求证:MF∥EN,MF=EN,
10、如图,在 ABCD中,3AB=2AD,E1、E2、E3、E4、E5依次是CB上的五个点,并且CE1=E1E2=E2E3=E3E4=E4E5=E5B,在三个结论中,(1)BE3⊥AE3,(2)AE2⊥DE4,(3)AE2⊥DE2之中,正确的个数是 。
5题
创新思维
如图,C为线段AB的中点,以AC及BC为对角线作平行四边形ADCE和BFCG,再作平行四边形CDHF及CEKG。
求证:H、C、K三点共线。
B
A
F
D
N
M
E
C
A
B
F
C
G
B
H
E
A
C
E
M
N
E
D
C
B
F
A
B
A
O
C
M
D
E
C
D
A
F
B
A
M
E
B
F
N
C
D
A
D
C
B
E1
E2
E3
E4
E5
C
K
E
A
D
G
B
F
H
B
P
M
C
N
A
D
C
E
B
G
F
A
图4-50
图4-49
B
C
D
E
F
A
B
D
C
F
E
G
A
D
C
E
B
F
A
B
C
D
E
F
A
O
B
C
D
M
A
D
P
G
C
B
E
F
A
D
C
F
B
E
A
D
1
2
