第24章《圆》单元测试卷（含解析）

中小学教育资源及组卷应用平台
人教版2022年九年级上册第24章《圆》单元测试卷
一、选择题(共30分)
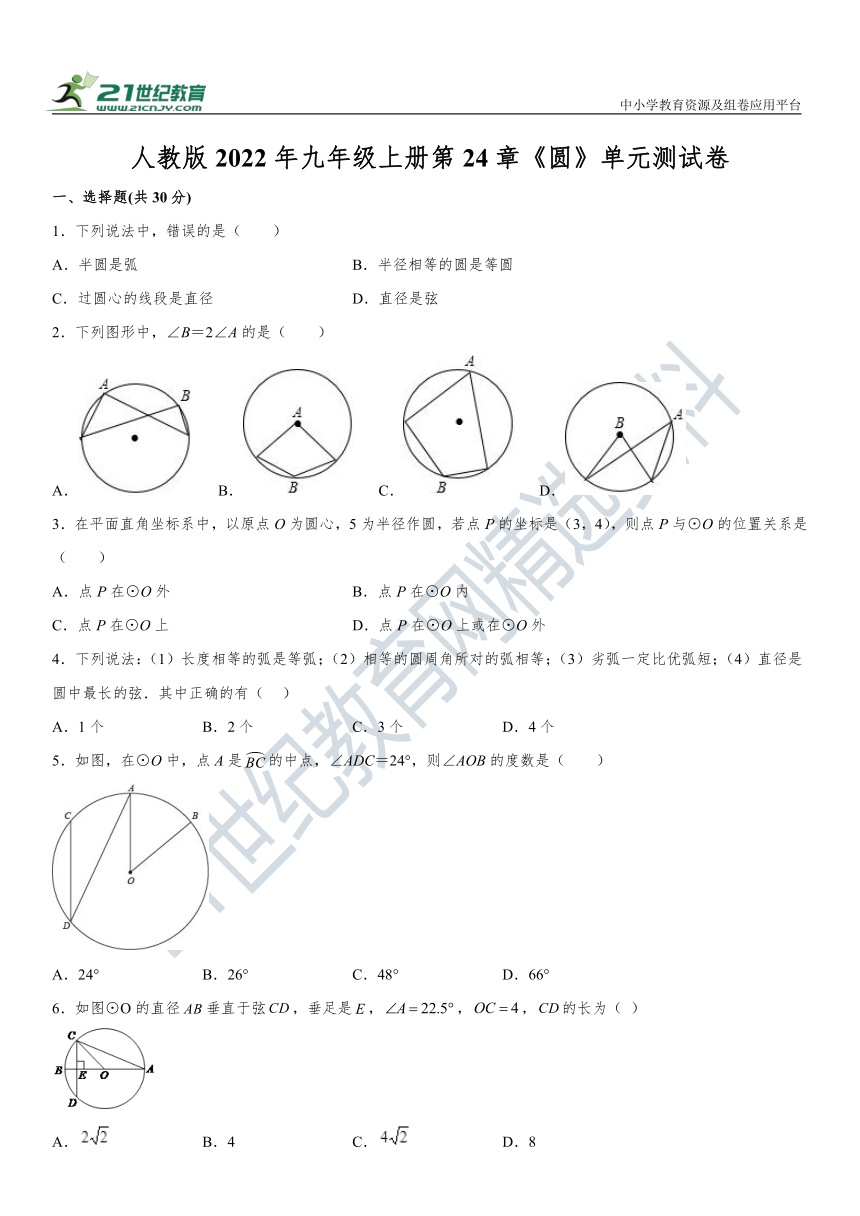
1．下列说法中，错误的是（　　）
A．半圆是弧 B．半径相等的圆是等圆
C．过圆心的线段是直径 D．直径是弦
2．下列图形中，∠B＝2∠A的是（　　）
A． B． C． D．
3．在平面直角坐标系中，以原点O为圆心，5为半径作圆，若点P的坐标是（3，4），则点P与⊙O的位置关系是（　　）
A．点P在⊙O外 B．点P在⊙O内
C．点P在⊙O上 D．点P在⊙O上或在⊙O外
4．下列说法：（1）长度相等的弧是等弧；（2）相等的圆周角所对的弧相等；（3）劣弧一定比优弧短；（4）直径是圆中最长的弦．其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
5．如图，在⊙O中，点A是的中点，∠ADC＝24°，则∠AOB的度数是（　　）
A．24° B．26° C．48° D．66°
6．如图⊙O的直径垂直于弦，垂足是，，，的长为（ ）
A． B．4 C． D．8
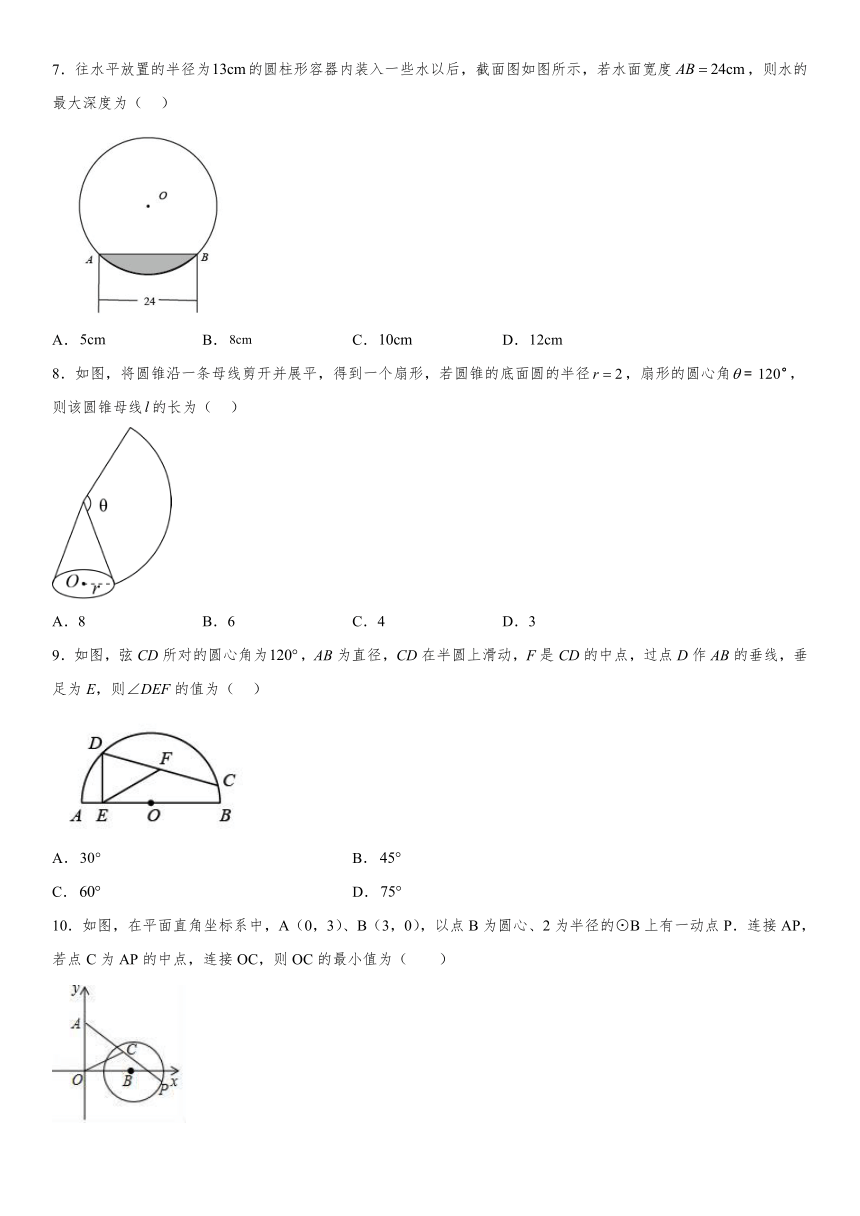
7．往水平放置的半径为的圆柱形容器内装入一些水以后，截面图如图所示，若水面宽度，则水的最大深度为（ ）
A． B． C． D．
8．如图，将圆锥沿一条母线剪开并展平，得到一个扇形，若圆锥的底面圆的半径，扇形的圆心角，则该圆锥母线的长为（ ）
A．8 B．6 C．4 D．3
9．如图，弦CD所对的圆心角为，AB为直径，CD在半圆上滑动，F是CD的中点，过点D作AB的垂线，垂足为E，则∠DEF的值为（ ）
A． B．
C． D．
10．如图，在平面直角坐标系中，A（0，3）、B（3，0），以点B为圆心、2为半径的⊙B上有一动点P．连接AP，若点C为AP的中点，连接OC，则OC的最小值为（　　）
A．1 B．2﹣1 C． D．﹣1
二、填空题(共15分)
11．若四边形ABCD是⊙O的内接四边形，∠A＝120°，则∠C的度数是___．
12．正八边形的中心角等于______度
13．如图，⊙O是△ABC的内切圆，⊙O切BC于点D，BD=3，CD=2，△ABC的周长为14，则AB=__．
14．如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F，设∠A=α，则∠E+∠F=______(用含α的式子表示)．
15．如图，已知在△ABC中，AB=AC=12．以AB为直径作半圆O，交BC于点D．若∠BAC=30°，则的长_____．
三、解答题(共75分)
16．(7分)如图，点A、B、C、D在⊙O上，∠ADC=60°，．请判断△ABC的形状，并说明理由．
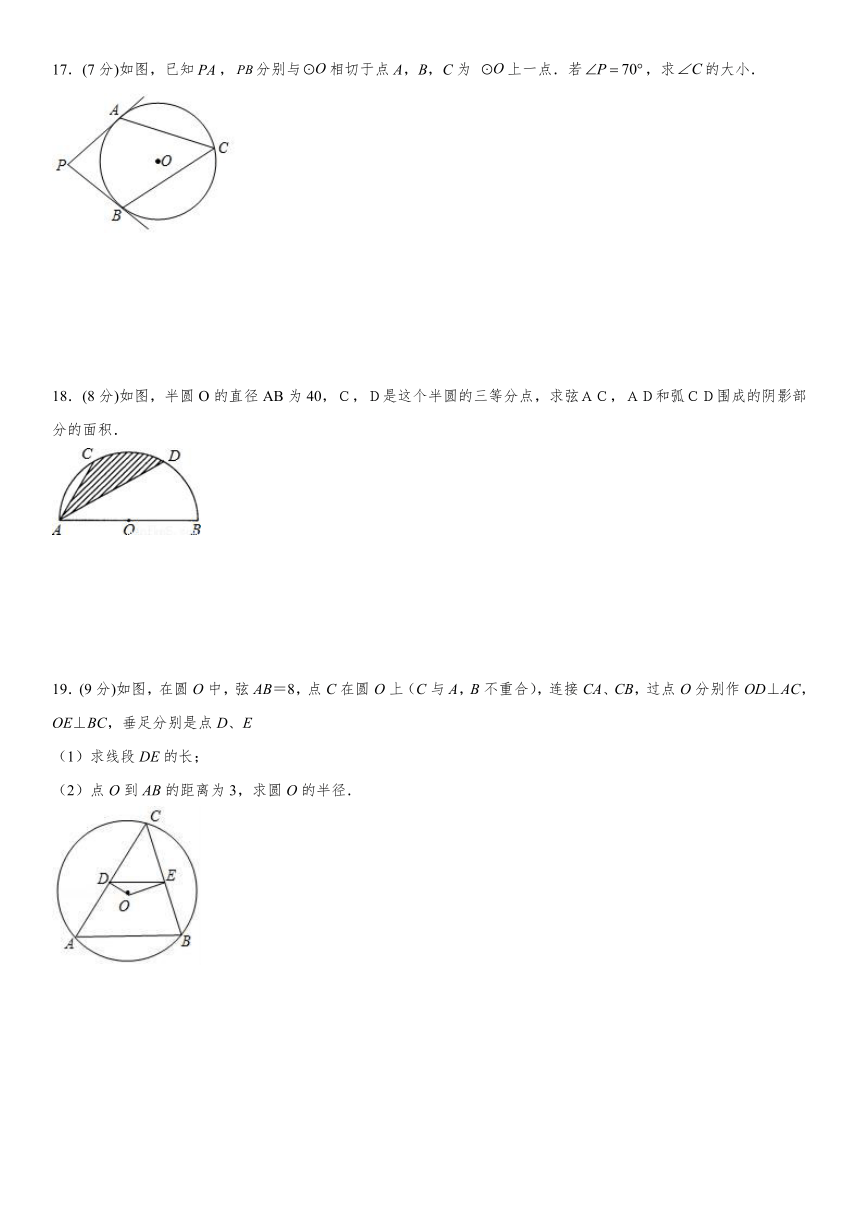
17．(7分)如图，已知，分别与相切于点A，B，C为 上一点．若，求的大小．
18．(8分)如图，半圆O的直径AB为40，Ｃ，Ｄ是这个半圆的三等分点，求弦ＡＣ，ＡＤ和弧ＣＤ围成的阴影部分的面积．
19．(9分)如图，在圆O中，弦AB＝8，点C在圆O上（C与A，B不重合），连接CA、CB，过点O分别作OD⊥AC，OE⊥BC，垂足分别是点D、E
（1）求线段DE的长；
（2）点O到AB的距离为3，求圆O的半径．
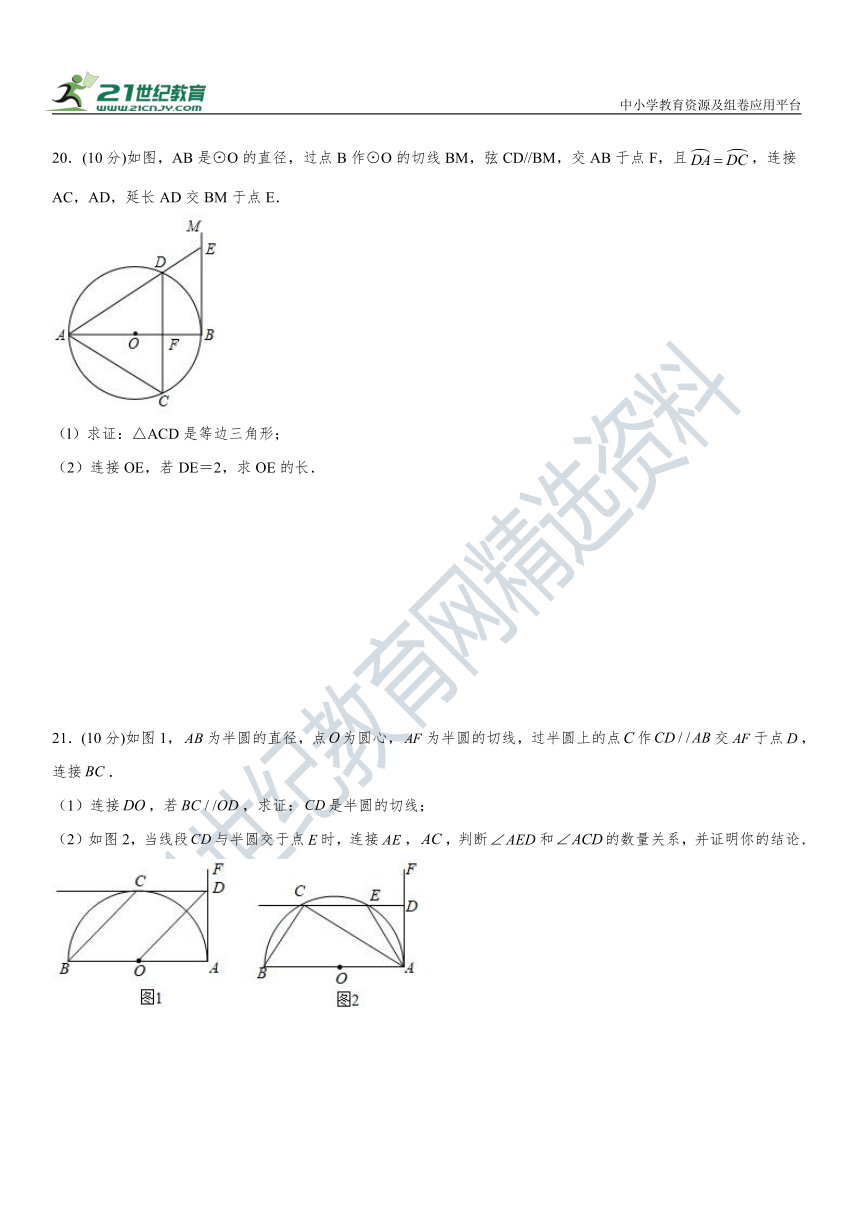
20．(10分)如图，AB是⊙O的直径，过点B作⊙O的切线BM，弦CD//BM，交AB于点F，且，连接AC，AD，延长AD交BM于点E．
（l）求证：△ACD是等边三角形；
（2）连接OE，若DE＝2，求OE的长．
21．(10分)如图1，为半圆的直径，点为圆心，为半圆的切线，过半圆上的点作交于点，连接．
（1）连接，若，求证：是半圆的切线；
（2）如图2，当线段与半圆交于点时，连接，，判断和的数量关系，并证明你的结论．
22．(12分)已知⊙O的半径为2，∠AOB=120°．
（1）点O到弦AB的距离为　　；．
（2）若点P为优弧AB上一动点（点P不与A、B重合），设∠ABP=α，将△ABP沿BP折叠，得到A点的对称点为A′；
①若∠α=30°，试判断点A′与⊙O的位置关系；
②若BA′与⊙O相切于B点，求BP的长；
③若线段BA′与优弧APB只有一个公共点，直接写出α的取值范围．
23．(12分)如图，为的外接圆，，点D是上的动点，且点分别位于的两侧．
（1）求的半径；
（2）当时，求的度数；
（3）设的中点为M，在点D的运动过程中，线段是否存在最大值？若存在，求出的最大值；若不存在，请说明理由．
参考答案
1．C
【分析】根据圆的有关概念进行判断．
【详解】解：A、半圆是弧，所以A选项的说法正确；
B、半径相等的圆是等圆，所以B选项的说法正确；
C、过圆心的弦为直径，所以C选项的说法错误；
D、直径是弦，所以D选项的说法正确．
故选C．
【点睛】考查了圆的认识：熟练掌握与圆有关的概念（ 弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．
2．D
【分析】根据圆周角定理对各选项进行逐一分析即可．
【详解】解：A中，∠A=∠B；
B中，∠A与∠B的大小无法判定；
C中，∠A+∠B=180°；
D中，∠B=2∠A．
故选D．
【点睛】考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
3．C
【分析】先求出点P与原点O的距离，然后再根据点与圆的位置关系进行判断即可.
【详解】∵点P的坐标是(3，4)，
∴OP==5，
而⊙O的半径为5，
∴OP等于圆的半径，
∴点P在⊙O上，
故选C．
【点睛】考查了点与圆的位置关系，关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
4．A
【分析】利用等弧的定义、圆周角定理、弧的定义及弦的定义分别判断后即可确定正确的选项．
【详解】解：（1）长度相等的弧不一定是等弧，弧的度数必须相同，故错误；
（2）同圆或等圆中相等的圆心角所对的弧相等，故错误；
（3）同圆或等圆中劣弧一定比优弧短，故错误；
（4）直径是圆中最长的弦，正确，
综上所述，四个说法中正确的只有1个，
故选：A．
【点睛】考查圆中有关定义，能够熟练掌握圆的有关知识是解答的关键．
5．C
【分析】直接利用圆周角求解．
【详解】解：∵点A是的中点，
∴，
∴∠AOB=2∠ADC=2×24°=48°．
故选：C．
【点睛】考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
6．C
【详解】∵直径AB垂直于弦CD，
∴CE=DE=CD，
∵∠A=22.5°，
∴∠BOC=45°，
∴OE=CE，
设OE=CE=x(x>0)，
∵OC=4，
∴x2+x2=16，
解得：x=2，
即：CE=2，
∴CD=4，
故选：C．
7．B
【分析】连接OA，过点O作OD⊥AB交AB于点C交⊙O于D，再根据勾股定理求出AC的长，进而可得出CD的长．
【详解】解：连接OA，过点O作OD⊥AB交AB于点C交⊙O于D，
∵OC⊥AB，由垂径定理可知，
∴AC=CB=AB=12，
在Rt△AOC中，由勾股定理可知：
∴，
∴，
故选：B．
【点睛】考查了垂径定理及勾股定理的应用，属于基础题，关键是过O点作AB的垂线，由此即可求解．
8．B
【分析】利用圆锥的侧面展开图为一个扇形，这个扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长，结合弧长公式得到，最后解关于的方程即可．
【详解】根据题意得
解得，，
即该圆锥的母线的长为6．
故答案为6．
【点睛】考查了关于圆锥的计算，掌握“圆锥的侧面展开图为一个扇形，这个扇形的弧长等于圆锥圆锥底面圆的周长，扇形的半径等于圆锥的母线长”是解决这个问题的关键．
9．C
【分析】连接，先根据等腰三角形的三线合一可得，，再判断出点四点共圆，然后根据圆周角定理即可得．
【详解】解：如图，连接，
弦所对的圆心角为，
，
，且点是的中点，
，（等腰三角形的三线合一），
又，
点四点共圆，
则由圆周角定理得：，
故选：C．
【点睛】考查了等腰三角形的性质、圆周角定理等知识点，熟练掌握圆周角定理是解题关键．
10．D
【分析】确定点C的运动路径是:以D为圆心,以为半径的圆,当O、C、D共线时, OC的长最小,先求D的半径为1 ,说明D是AB的中点, 根据直角三角形斜边中线是斜边一半可得OD=,所以OC的最小值是.
【详解】当点P运动到AB的延长线上时,即如图中点, 是的中点，
当点P在线段AB上时, 是中点,取的中点为D，
点C的运动路径是以D为圆心,以D为半径的圆(CA: PA=1 : 2 ,则点C轨迹和点P轨迹相似,所以点C的轨迹就是圆) , 当O、C、D共线时, OC的长最小，设线段AB交B于Q，
中，OA=3,OB=3,
.
半径为2,
是的中点,
是的中点,
即半径为1,
故选D.
【点睛】考查了图形与坐标的性质、勾股定理、直角三角形斜边上的中线等于斜边的一半的性质、圆的性质、两点之间线段最短,确定出OC最小时点C的位置是解题关键, 也是的难点
11．60°．
【分析】根据圆内接四边形对角互补进行求解即可得.
【详解】∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠C=180°，
∴∠C=180°﹣∠A=60°，
故答案为60°．
【点睛】考查了圆内接四边形的性质，熟练掌握是解题的关键.
12．45
【分析】已知该多边形为正八边形，代入中心角公式即可得出．
【详解】∵该多边形为正八边形，故n=8
∴
故答案为：45．
【点睛】考查了正多边形的中心角，把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆．正多边形每一边所对的圆心角叫做正多边形的中心角，正n边形的每个中心角都等于．
13．5
【分析】如图所示：由切线长定理可知：BE=BD=3，CD=CF=2，AE=AF，然后根据△ABC的周长为14求解即可．
【详解】解：如图所示：
由切线长定理可知：BE=BD=3，CD=CF=2，AE=AF．
设AE=AF=x．
根据题意得：2x+3+3+2+2=14．
解得：x=2．
∴AE=2．
∴AB=BE+AE=3+2=5．
故答案为；5．
【点睛】主要考查的是三角形的内切圆，利用切线长定理得到BE=BD=3，CD=CF=2，AE=AF是解题的关键．
14．180°﹣2α．
【分析】根据圆内接四边形的性质得到∠ADC+∠ABC=180°，∠ECD=∠A=，∠BCF=∠A=，根据三角形内角和定理计算即可．
【详解】∵四边形ABCD内接于⊙O，
∴∠ADC+∠ABC=180°，∠ECD=∠A=，∠BCF=∠A=，
∴∠EDC+∠FBC=180°，
∴∠E+∠F=360°-180°-2=180°-2，
故答案为180°-2．
【点睛】考查的是圆内接四边形的性质、三角形内角和定理，掌握圆内接四边形的对角互、圆内接四边形的任意一个外角等于它的内对角是解题的关键．
15．5π
【分析】连接AD，由等腰△ABC中，AB=AC，以AB为直径的半圆交BC于点D，可得∠BAD=∠CAD=15°，即可得∠ABD=75°，继而求得∠AOD的度数，则可求得弧AD的度数，进而利用弧长公式计算即可．
【详解】解：连接AD、OD，
∵AB为直径，
∴∠ADB=90°，
即AD⊥BC，
∵AB=AC，
∴∠BAD=∠CAD=∠BAC=15°，BD=DC，
∴∠ABD=75°，
∴∠AOD=150°,
∴弧AD的度数为150°，
∴弧AD的长==5π.
故答案为5π.
【点睛】考查的是弧长的计算，掌握弧长公式l=、圆周角定理和等腰三角形的性质是解题的关键．
16．△ABC是等边三角形，理由见解析.
【分析】由圆周角定理可知∠ADC=∠ABC=∠BAC=∠BDC=60°，再由三角形内角和定理可知∠ACB=60°，故可得出结论
【详解】△ABC是等边三角形，
理由：∵
∴AC=BC，
∵∠ADC=60°，
∴∠ABC=∠ADC=60°，
∴△ABC是等边三角形．
【点睛】考查的是圆周角定理，等边三角形的判定，熟练掌握圆周角定理是解答此题的关键．
17．55°
【分析】连接OA、OB，根据切线的性质可得∠OAP=∠OBP=90°，利用四边形的内角和即可求出∠AOB，最后利用圆周角定理即可求出结论．
【详解】解：连接OA、OB
∵，分别与相切于点A，B，
∴∠OAP=∠OBP=90°，
∵
∴∠AOB=360°－∠OAP－∠OBP－∠P=110°
∴∠C=∠AOB=55°．
【点睛】此题考查的是切线的性质和圆周角定理，掌握切线的性质和圆周角定理是解题关键．
18．cm2
【分析】连接CO、OD，CD，根据条件证明CD∥AB，然后可得△OCD与△CDA面积相等，从而阴影部分的面积转化为扇形OCD的面积．
【详解】试题分析：
试题解析：连接CO、OD，CD，如图;
∵C、D是这个半圆的三等分点，
∴CD∥AB，∠CDO=60°，
∴∠CAD =30°，
∵OC=OD，∴△OCD是等边三角形，CD=OC=AB=20，
∴△OCD与△CDA是等底等高的三角形，
∴=cm2．
答：阴影部分的面积S是cm2．
19．（1）DE＝4；（2）圆O的半径为5．
【分析】（1）根据垂径定理得出AD=DC，CE=EB，再根据三角形的中位线定理可得DE=AB，代入相应数值求出即可；
（2）过点O作OH⊥AB，垂足为点H，则OH=3，连接OA，根据垂径定理可得AH=4，在Rt△AHO中，利用勾股定理求出AO的长即可得答案．
【详解】（1）∵OD经过圆心O，OD⊥AC，
∴AD=DC，
同理：CE=EB，
∴DE是△ABC的中位线，
∴DE=AB，
∵AB=8，
∴DE=4；
（2）过点O作OH⊥AB，垂足为点H，则OH=3，连接OA，
∵OH经过圆心O，
∴AH=BH=AB，
∵AB=8，
∴AH=4，
在Rt△AHO中，AH2+OH2=AO2，
∴AO=5，即圆O的半径为5．
【点睛】主要考查了垂径定理，涉及了三角形中位线定理、勾股定理等内容，熟练掌握垂径定理是解的关键．
20．（1）见解析；（2）
【分析】（1）根据切线的定义可知AB⊥BM，又∵BM//CD，∴AB⊥CD，根据圆的对称性可得AD=AC，再根据等弧对等弦得DA=DC，即DA=DC=AC，所以可得△ACD是等边三角形；
（2）△ACD为等边三角形，AB⊥CD，由三线合一可得∠DAB=30°，连接BD，根据直径所对的角是直角和三角形的内角和可得∠∠EBD＝∠DAB＝30°，因为DE＝2，求出BE＝4，根据勾股定理得，直角三角形中30°角所对的直角边等于斜边的一半得，，，在Rt△OBE中，根据勾股定理即可得出OE的长．
【详解】解：（1）∵BM是⊙O切线，AB为⊙O直径，
∴AB⊥BM，
∵BM//CD，
∴AB⊥CD，
∴AD＝AC，
∴AD＝AC，
∴DA＝DC，
∴DC＝AD，
∴AD＝CD＝AC，
∴△ACD为等边三角形.
（2）△ACD为等边三角形，AB⊥CD，
∴∠DAB＝30°，
连结BD，
∴BD⊥AD.
∠EBD＝∠DAB＝30°，
∵DE＝2，
∴BE＝4，，，，
在Rt△OBE中，．
【点睛】考查圆的有关性质，直角三角形的性质；勾股定理．
21．（1）见解析；（2）
【分析】（1）连接，根据切线的性质得到，推出四边形是平行四边形，得到，等量代换得到，推出四边形是平行四边形，根据平行四边形的性质得到，于是得到结论；
（2）如图2，连接，根据圆周角定理得到，求得，证得，等量代换即可得到结论．
【详解】（1）证明：连接，
为半圆的切线，为半圆的直径，
，
，，
四边形是平行四边形，
，
，
，
四边形是平行四边形，
，
，
，
，
，
是半圆的切线；
（2）解：，
理由：如图2，连接，
为半圆的直径，
，
，
，
，
，
，
，
．
【点睛】考查了切线的判定和性质，圆周角定理，平行四边形的判定和性质，正确的作出辅助线是解题的关键．
22．（1）1；（2）①点A′在⊙O上；②；③0°＜α＜30°或60°≤α＜120°
【分析】（1）如图，作辅助线；证明∠AOC=60°，得到OC=1．
（2）①证明∠PAB=90°，得到PB是⊙O的直径；证明∠PA′B=90°，即可解决问题．
②证明∠A′BP=∠ABP=60°；借助∠APB=60°，得到△PAB为正三角形，求出AB的长即可解决问题．
③直接写出α的取值范围即可解决问题．
【详解】
解：（1）如图，过点O作OC⊥AB于点C；
∵OA=OB，
则∠AOC=∠BOC=×120°=60°，
∵OA=2，
∴OC=1．
故答案为1．
（2）①∵∠AOB=120°
∴∠APB=∠AOB=60°，
∵∠PBA=30°，
∴∠PAB=90°，
∴PB是⊙O的直径，
由翻折可知：∠PA′B=90°，
∴点A′在⊙O上．
②由翻折可知∠A′BP=∠ABP，
∵BA′与⊙O相切，
∴∠OBA′=90°，
∴∠ABA′=120°，
∴∠A′BP=∠ABP=60°；
∵∠APB=60°，
∴△PAB为正三角形，
∴BP=AB；
∵OC⊥AB，
∴AC=BC；而OA=2，OC=1，
∴AC=，
∴BP=AB=2．
③α的取值范围为0°＜α＜30°或60°≤α＜120°．
【点睛】该题主要考查了翻折变换、垂径定理及其应用问题；解题的关键是灵活运用翻折变换、垂径定理等几何知识点来分析、判断、推理或解答．
23．（1）4；（2）15°；（3）存在，
【分析】（1）利用勾股定理求出AB即可．
（2）连接OC，OD，证明∠OCA＝60°，∠OCD＝45°，可得结论．
（3）如图2中，连接OM，OC．证明OM⊥AD，推出点M的运动轨迹以AO为直径的⊙J，连接CJ，JM．求出CJ．JM，根据CM≤CJ+JM＝22，可得结论．
【详解】解：（1）如图1中，
∵AB是直径，
∴∠ACB＝90°，
∵AC＝4，BC＝4，
∴AB8，
∴⊙O的半径为4．
（2）如图1中，连接OC，OD．
∵CD＝4，OC＝OD＝4，
∴CD2＝OC2+OD2，
∴∠COD＝90°，
∴∠OCD＝45°，
∵AC＝OC＝OA，
∴△AOC是等边三角形，
∴∠ACO＝60°，
∴∠ACD＝∠ACO﹣∠DCO＝60°﹣45°＝15°．
（3）如图2中，连接OM，OC．
∵AM＝MD，
∴OM⊥AD，
∴点M的运动轨迹以AO为直径的⊙J，
连接CJ，JM．
∵△AOC是等边三角形，AJ＝OJ，
∴CJ⊥OA，
∴CJ2，
∵CM≤CJ+JM＝22，
∴CM的最大值为22．
【点睛】属于圆综合题，考查了圆周角定理，垂径定理，等边三角形的判定和性质，等腰直角三角形的判定和性质，解直角三角形等知识，解题的关键是寻找特殊三角形解决问题，正确寻找点M的运动轨迹，属于中考压轴题．