平行四边形的判定(第二课时)[下学期]
文档属性
| 名称 | 平行四边形的判定(第二课时)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-10 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
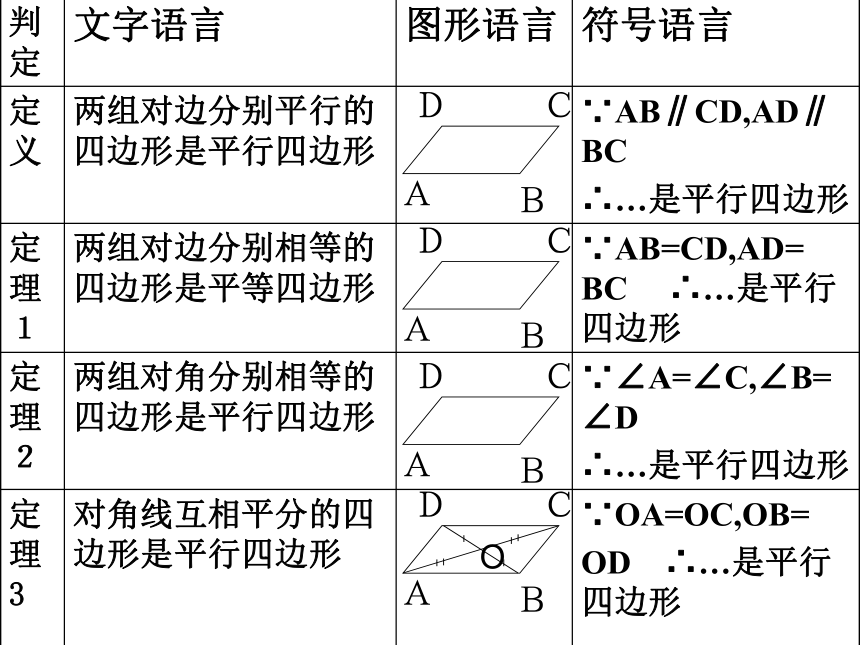
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴…是平行四边形
定理1 两组对边分别相等的四边形是平等四边形 ∵AB=CD,AD= BC ∴…是平行四边形
定理2 两组对角分别相等的四边形是平行四边形 ∵∠A=∠C,∠B=∠D
∴…是平行四边形
定理3 对角线互相平分的四边形是平行四边形
∵OA=OC,OB=
OD ∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
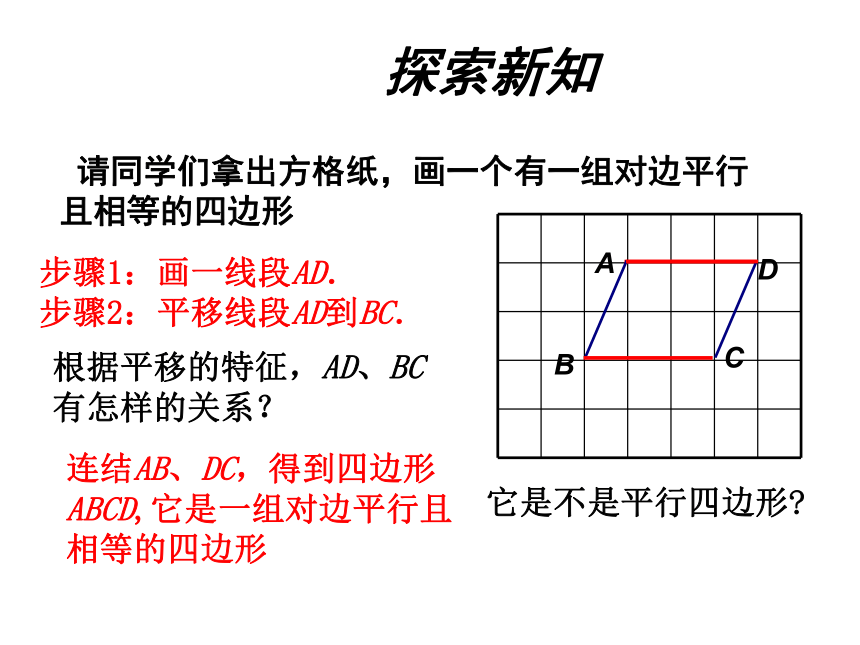
探索新知
请同学们拿出方格纸,画一个有一组对边平行且相等的四边形
步骤1:画一线段AD.
步骤2:平移线段AD到BC.
根据平移的特征,AD、BC有怎样的关系?
连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形
它是不是平行四边形
C
B
D
A
A
B
C
D
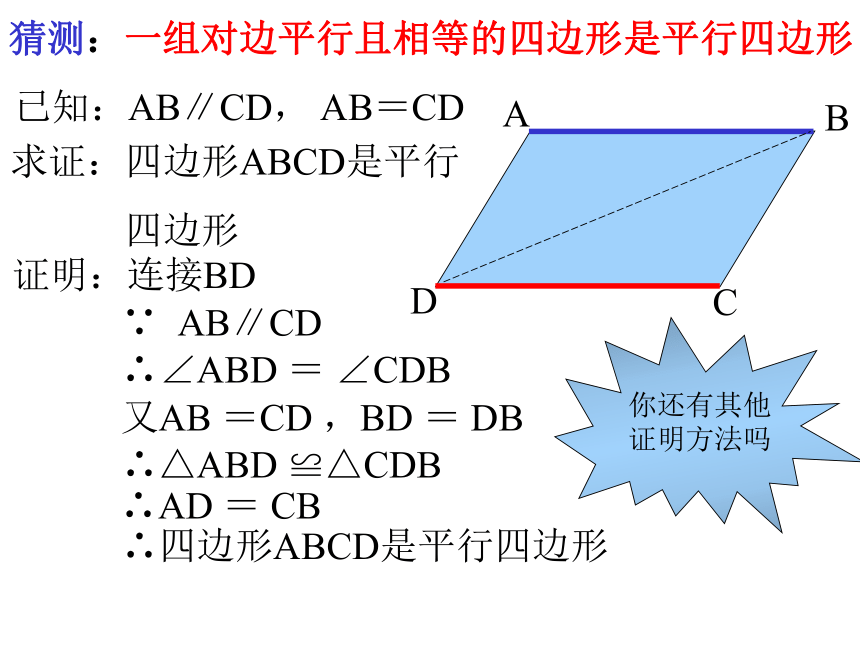
猜测:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行
四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又AB =CD ,BD = DB
∴△ABD ≌△CDB
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
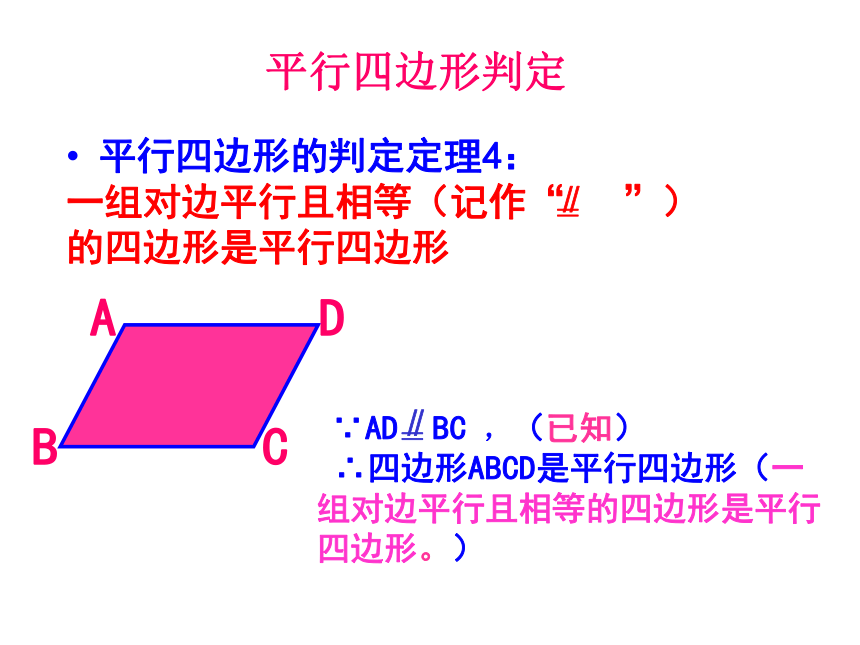
平行四边形判定
平行四边形的判定定理4:
一组对边平行且相等(记作“ ”)
的四边形是平行四边形
A
B
C
D
=
∥
∵AD BC ,(已知)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。)
=
∥
探索新知
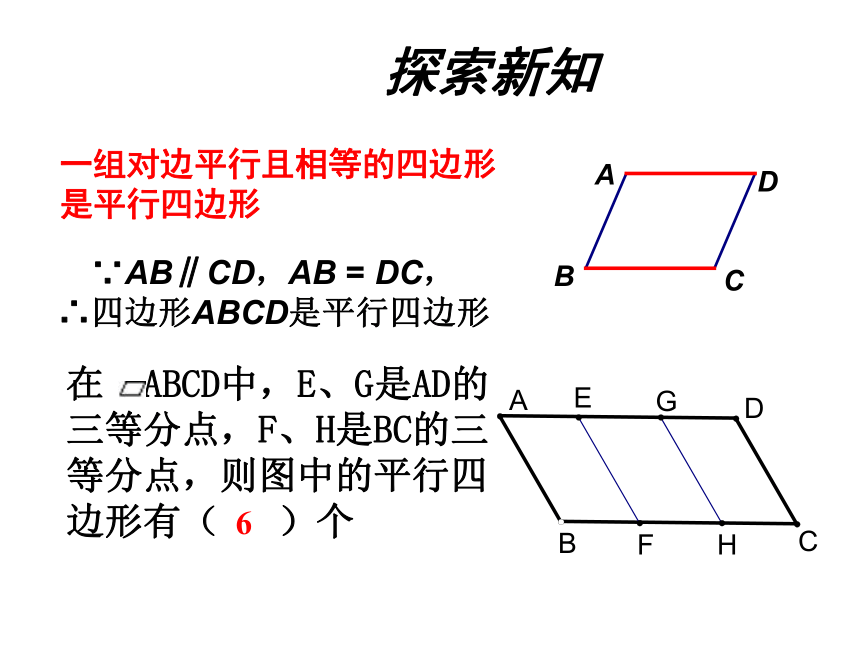
一组对边平行且相等的四边形是平行四边形
∵AB∥CD,AB = DC,
∴四边形ABCD是平行四边形
C
B
D
A
在 ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有( )个
6
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两组对角分别相等的四边形是平行四边形;
4.两条对角线互相平分的四边形是平行四边形;
5.一组对边平行且相等的四边形是平行四边形。
平行四边形的判定方法:
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
平行四边形的判定方法共有几种?
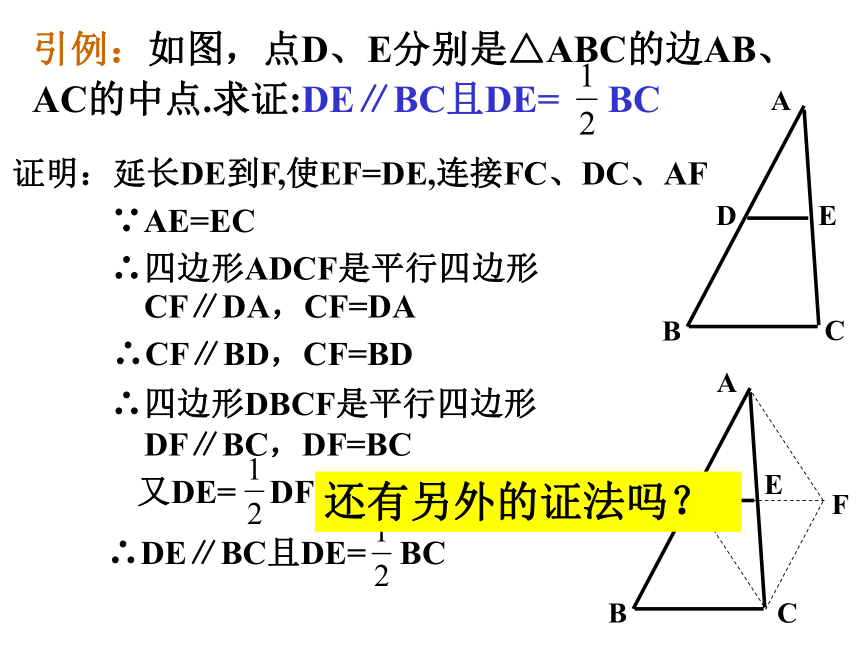
引例:如图,点D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC且DE= BC
A
B
C
D
E
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
还有另外的证法吗?
A
B
C
D
E
F
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
引例:如图,点D、E分别是△ABC的边AB、AC的中点.求证: DE∥BC且DE= BC
定义:把连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
中位线定理
证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
三角形的中位线与三角形的中线有什么区别?
中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。
巩固练习:
1.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
B
A
F
E
D
C
三条中位线把原三角形分成了几个小三角形?这些三角形有什么关系?
2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?
A
B
C
D
E
例1:求证顺次连结四边形各边中点所得的四边形是平行四边形。
已知:E、F、G、H分别是四边形ABCD中AB、
BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
任意四边形四边中点连线所得的四边形一定是平行四边形。
例2:已知点D、E、F分别在 ABC的边BC、AB、AC上,且DE AF,DE=AF,G在FD的延长线上,DG=DF。
求证:AG与ED互相平分。
练一练:
1、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形
2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
1
2
3
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180
A
B
C
D
D
5、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④
D
A
B
C
D
如图,在 ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。
A
D
C
B
E
F
G
H
O
小结:
1、你到今天为止共学到了几种判定平行四边形的方法?
2、你能够灵活运用吗?
四边形
两组对边分别平行
对角线互相平分
一组对边平行且相等
平行四边形
两组对边分别相等
两组对角分别相等
判定 文字语言 图形语言 符号语言
定义 两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴…是平行四边形
定理1 两组对边分别相等的四边形是平等四边形 ∵AB=CD,AD= BC ∴…是平行四边形
定理2 两组对角分别相等的四边形是平行四边形 ∵∠A=∠C,∠B=∠D
∴…是平行四边形
定理3 对角线互相平分的四边形是平行四边形
∵OA=OC,OB=
OD ∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
探索新知
请同学们拿出方格纸,画一个有一组对边平行且相等的四边形
步骤1:画一线段AD.
步骤2:平移线段AD到BC.
根据平移的特征,AD、BC有怎样的关系?
连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形
它是不是平行四边形
C
B
D
A
A
B
C
D
猜测:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD, AB=CD
求证:四边形ABCD是平行
四边形
证明:连接BD
∵ AB∥CD
∴∠ABD = ∠CDB
又AB =CD ,BD = DB
∴△ABD ≌△CDB
∴AD = CB
∴四边形ABCD是平行四边形
你还有其他证明方法吗
平行四边形判定
平行四边形的判定定理4:
一组对边平行且相等(记作“ ”)
的四边形是平行四边形
A
B
C
D
=
∥
∵AD BC ,(已知)
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。)
=
∥
探索新知
一组对边平行且相等的四边形是平行四边形
∵AB∥CD,AB = DC,
∴四边形ABCD是平行四边形
C
B
D
A
在 ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有( )个
6
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两组对角分别相等的四边形是平行四边形;
4.两条对角线互相平分的四边形是平行四边形;
5.一组对边平行且相等的四边形是平行四边形。
平行四边形的判定方法:
两组对边分别相等
两组对角分别相等
对角线互相平分
两组对边分别平行
一组对边平行且相等
四边形是平行四边形
边
角
对角线:
平行四边形的判定方法共有几种?
引例:如图,点D、E分别是△ABC的边AB、AC的中点.求证:DE∥BC且DE= BC
A
B
C
D
E
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
还有另外的证法吗?
A
B
C
D
E
F
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
引例:如图,点D、E分别是△ABC的边AB、AC的中点.求证: DE∥BC且DE= BC
定义:把连接三角形两边中点的线段叫做三角形的中位线。
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
中位线定理
证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
三角形的中位线与三角形的中线有什么区别?
中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。
巩固练习:
1.如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
B
A
F
E
D
C
三条中位线把原三角形分成了几个小三角形?这些三角形有什么关系?
2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?
A
B
C
D
E
例1:求证顺次连结四边形各边中点所得的四边形是平行四边形。
已知:E、F、G、H分别是四边形ABCD中AB、
BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
任意四边形四边中点连线所得的四边形一定是平行四边形。
例2:已知点D、E、F分别在 ABC的边BC、AB、AC上,且DE AF,DE=AF,G在FD的延长线上,DG=DF。
求证:AG与ED互相平分。
练一练:
1、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形
2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
1
2
3
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180
A
B
C
D
D
5、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④
D
A
B
C
D
如图,在 ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。
A
D
C
B
E
F
G
H
O
小结:
1、你到今天为止共学到了几种判定平行四边形的方法?
2、你能够灵活运用吗?
四边形
两组对边分别平行
对角线互相平分
一组对边平行且相等
平行四边形
两组对边分别相等
两组对角分别相等
