平行四边形的判定(第一课时)[下学期]
文档属性
| 名称 | 平行四边形的判定(第一课时)[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 268.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-10 00:00:00 | ||
图片预览


文档简介
(共21张PPT)
平行四边形的判定(1)
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
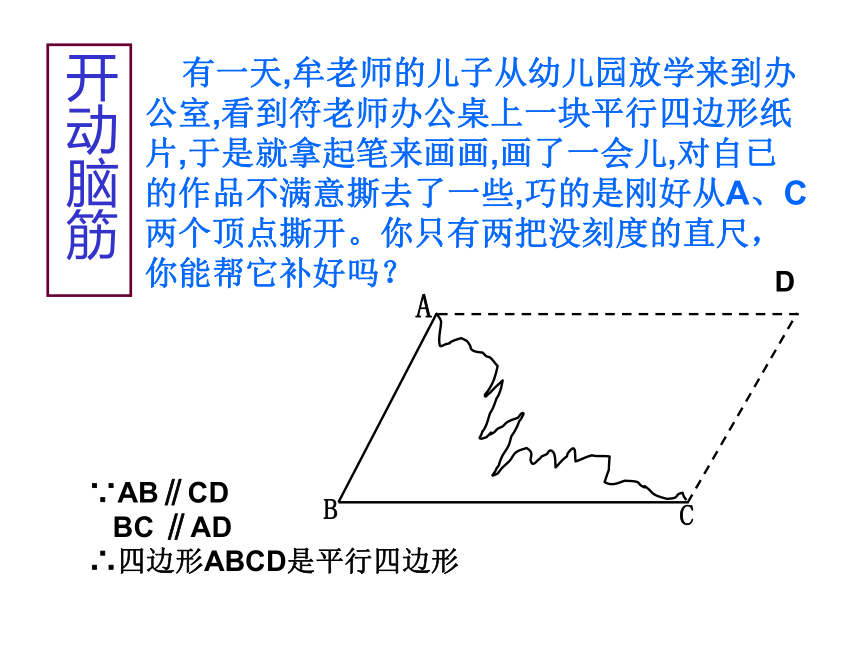
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
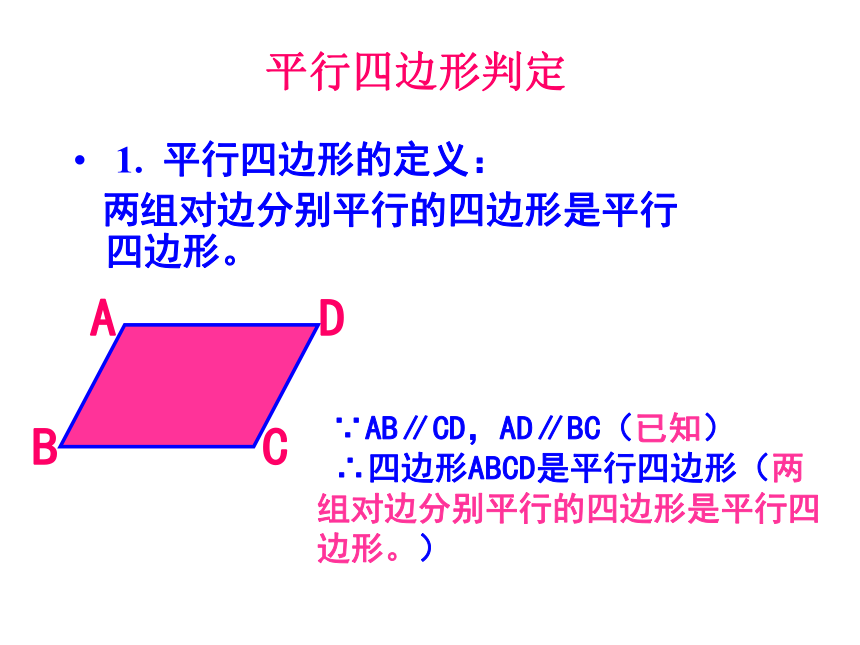
开动脑筋
有一天,牟老师的儿子从幼儿园放学来到办公室,看到符老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你只有两把没刻度的直尺,你能帮它补好吗?
A
B
C
D
∵AB∥CD
BC ∥AD
∴四边形ABCD是平行四边形
平行四边形判定
1. 平行四边形的定义:
两组对边分别平行的四边形是平行四边形。
A
B
C
D
∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两 组对边分别平行的四边形是平行四边形。)
学行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
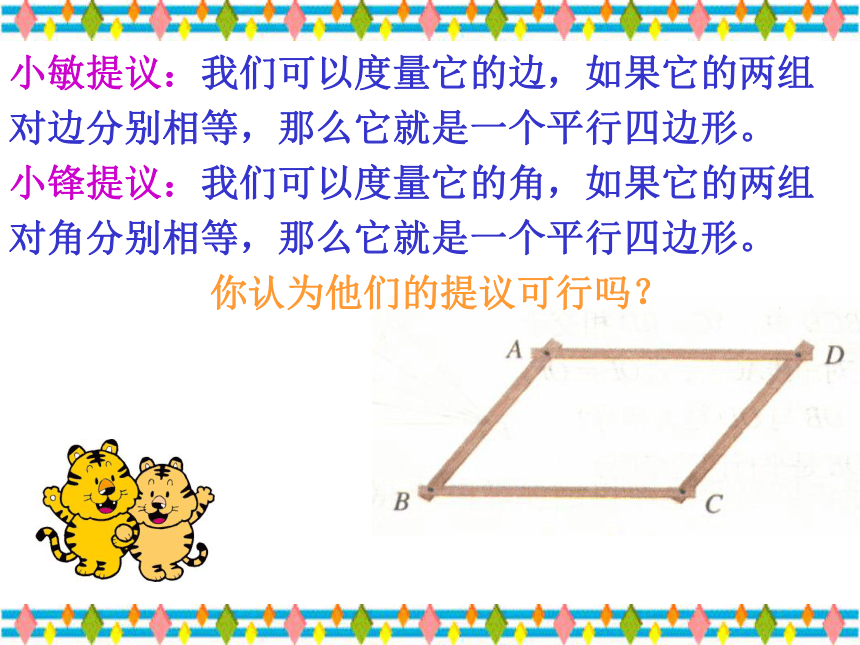
小敏提议:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形。
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
你认为他们的提议可行吗?
B
D
A
C
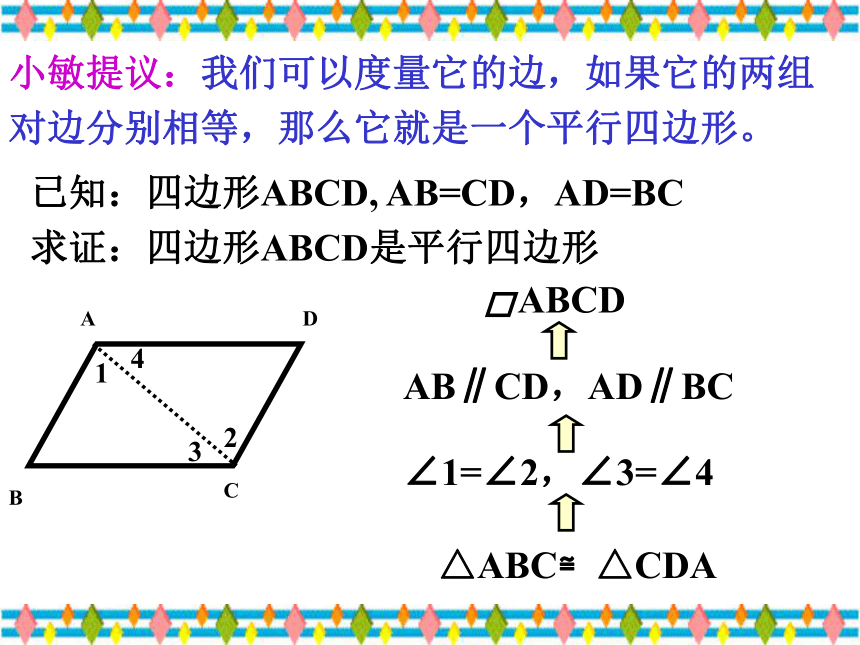
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
小敏提议:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形。
ABCD
AB∥CD,AD∥BC
2
1
3
4
∠1=∠2,∠3=∠4
△ABC≌△CDA
B
D
A
C
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
2
1
3
4
连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两 组对边分别相等的四边形是平行四边形。)
B
D
A
C
∠A+ ∠B=180 ° AD∥BC
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形
ABCD
∠A+ ∠D=180 ° AB∥CD
∠A+ ∠B +∠C+ ∠D =360 °
B
D
A
C
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
证明:
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∵ ∠A=∠C, ∠B=∠D (已知)
∴四边形ABCD是平行四边形(两 组对角分别相等的四边形是平行四边形。)
小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”
你认为小丽的做法有根据吗?
B
D
A
C
O
已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
4
2
1
3
证明:∵ AO = CO ,BO = DO ,∠1 = ∠2
∴△AOB≌△COD
∴AB ∥ CD
同理AD ∥ BC
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
∴ ∠3 = ∠4
平行四边形判定
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形。
∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形。)
B
D
A
C
O
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两组对角分别相等的四边形是平行四边形;
4.两条对角线互相平分的四边形是平行四边形。
平行四边形的判定方法:
老师说下列四边形是平行四边形,你相信吗?请说出理由
A
D
C
B
110°
70°
110°
(2)
⑴
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
(3)
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
两条对角线互相平分的四边形是 平行四边形。
大显身手
练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
请你识别下列四边形哪些是平行四边形
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
平行四边形的判定(1)
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
开动脑筋
有一天,牟老师的儿子从幼儿园放学来到办公室,看到符老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。你只有两把没刻度的直尺,你能帮它补好吗?
A
B
C
D
∵AB∥CD
BC ∥AD
∴四边形ABCD是平行四边形
平行四边形判定
1. 平行四边形的定义:
两组对边分别平行的四边形是平行四边形。
A
B
C
D
∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两 组对边分别平行的四边形是平行四边形。)
学行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
小敏提议:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形。
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
你认为他们的提议可行吗?
B
D
A
C
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
小敏提议:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形。
ABCD
AB∥CD,AD∥BC
2
1
3
4
∠1=∠2,∠3=∠4
△ABC≌△CDA
B
D
A
C
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
2
1
3
4
连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
证明:
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两 组对边分别相等的四边形是平行四边形。)
B
D
A
C
∠A+ ∠B=180 ° AD∥BC
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形
ABCD
∠A+ ∠D=180 ° AB∥CD
∠A+ ∠B +∠C+ ∠D =360 °
B
D
A
C
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
证明:
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∵ ∠A=∠C, ∠B=∠D (已知)
∴四边形ABCD是平行四边形(两 组对角分别相等的四边形是平行四边形。)
小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”
你认为小丽的做法有根据吗?
B
D
A
C
O
已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
4
2
1
3
证明:∵ AO = CO ,BO = DO ,∠1 = ∠2
∴△AOB≌△COD
∴AB ∥ CD
同理AD ∥ BC
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
∴ ∠3 = ∠4
平行四边形判定
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形。
∵ OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形。)
B
D
A
C
O
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两组对角分别相等的四边形是平行四边形;
4.两条对角线互相平分的四边形是平行四边形。
平行四边形的判定方法:
老师说下列四边形是平行四边形,你相信吗?请说出理由
A
D
C
B
110°
70°
110°
(2)
⑴
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
(3)
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
两条对角线互相平分的四边形是 平行四边形。
大显身手
练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
请你识别下列四边形哪些是平行四边形
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
