平行四边形的判定[下学期]
图片预览




文档简介
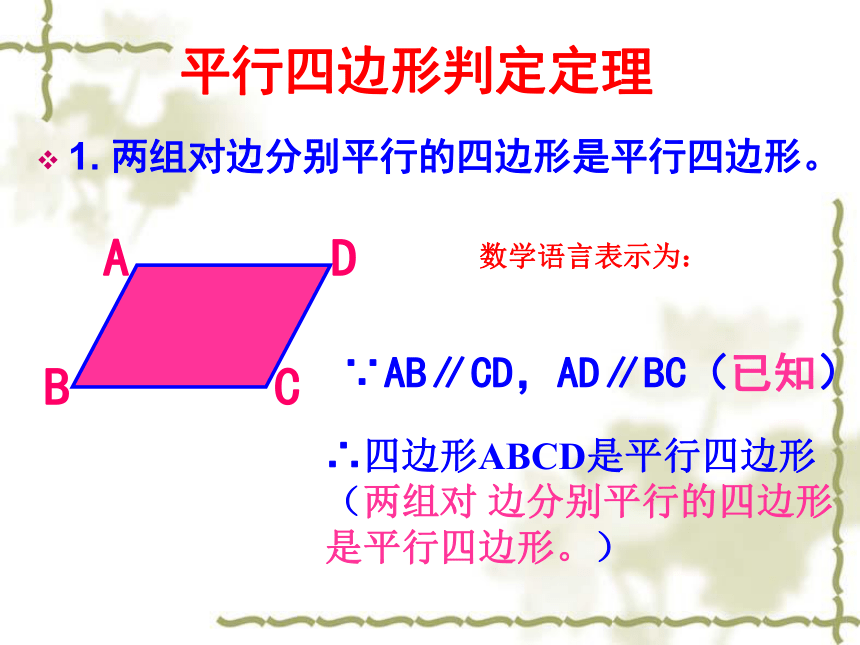
课件15张PPT。街头中学 李高明平行四边形的判定一☆定义:1、平行四边形对边分别相等2、平行四边形对角分别相等3、平行四边形对角线互相平分平行四边形的性质两组对边分别平行的四边形是平行四边形。☆ 性质:平行四边形的两组对边分别相等两组对边分别相等的四边形是平行四边形。平行四边形两组对角分别相等 两组对角分别相等的四边形是平行四边形。平行四边形对角线互相平分对角线互相平分的四边形是平行四边形。它的逆命题:它的逆命题:它的逆命题:平行四边形判定定理1. 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC(已知)数学语言表示为:∴四边形ABCD是平行四边形
(两组对 边分别平行的四边形
是平行四边形。)
学习了平行四边形后,余刚同学回家用硬纸条钉制了一个平行四边形。请你帮忙问:凭什么确定这四边形就是平行四边形呢?
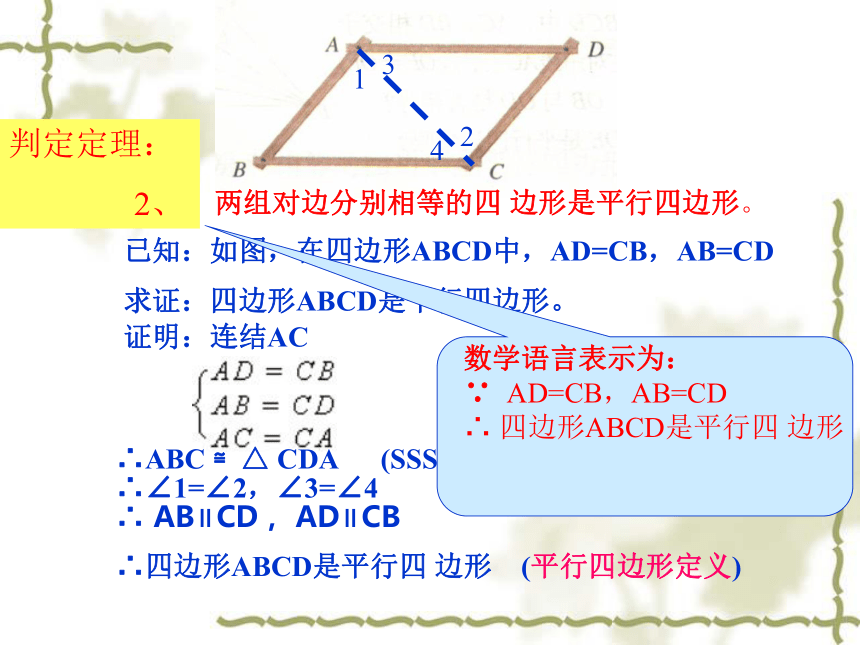
猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形ABCD中,AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS) ∴∠1=∠2,∠3=∠41234∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义)判定定理:
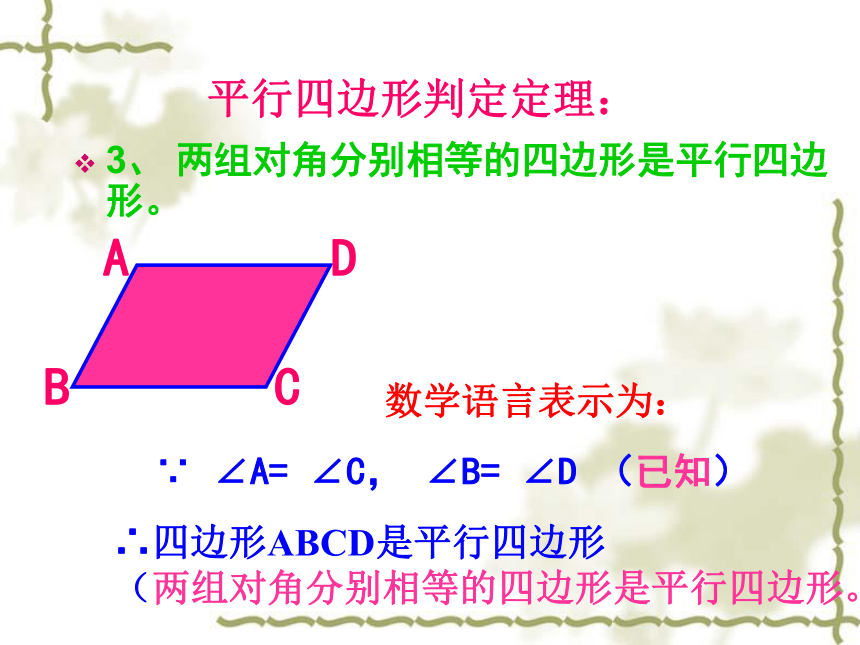
2、 平行四边形判定定理:3、 两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D (已知)数学语言表示为:∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形。)
4、对角线互相平分的四边形是平行四边形。 已知:如图,四边形ABCD的对角线AC,BD相交于点O,并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
你能根据上述判定定理证明平行四边形判定定理 :1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。4、对角线互相平分的四边形是平行四边形。 3、两组对角分别相等的四边形是平行四边形例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)O延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC. 某同学说:“只要给我一把尺,我就能判断
一个四边形是否为平行四边形。” 请你说出该
同学是怎样判断的。
是非题
1、有三个角是直角的四边形是平行四边形 2、有两组对边分别相等的四边形是平行四边形3、两条对角线相等的四边形是平行四边形 4、任意相邻两个角都互补的四边形是平行四边形 5、一组对边平行,另一组对边相等的四边形一定是平行四边形 6、有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形 ( √ )
( √ )
( ╳ )
( √ )(╳ )(╳ )
在平行四边形ABCD中,E、F为对角线BD上两点,且______,请添加一个条件,使四边形AECF是平行四边形。 通过了本节课学习,
你有哪些收获?同学们再见!
(两组对 边分别平行的四边形
是平行四边形。)
学习了平行四边形后,余刚同学回家用硬纸条钉制了一个平行四边形。请你帮忙问:凭什么确定这四边形就是平行四边形呢?
猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形ABCD中,AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS) ∴∠1=∠2,∠3=∠41234∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义)判定定理:
2、 平行四边形判定定理:3、 两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D (已知)数学语言表示为:∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形。)
4、对角线互相平分的四边形是平行四边形。 已知:如图,四边形ABCD的对角线AC,BD相交于点O,并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
你能根据上述判定定理证明平行四边形判定定理 :1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。4、对角线互相平分的四边形是平行四边形。 3、两组对角分别相等的四边形是平行四边形例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)O延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC. 某同学说:“只要给我一把尺,我就能判断
一个四边形是否为平行四边形。” 请你说出该
同学是怎样判断的。
是非题
1、有三个角是直角的四边形是平行四边形 2、有两组对边分别相等的四边形是平行四边形3、两条对角线相等的四边形是平行四边形 4、任意相邻两个角都互补的四边形是平行四边形 5、一组对边平行,另一组对边相等的四边形一定是平行四边形 6、有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形 ( √ )
( √ )
( ╳ )
( √ )(╳ )(╳ )
在平行四边形ABCD中,E、F为对角线BD上两点,且______,请添加一个条件,使四边形AECF是平行四边形。 通过了本节课学习,
你有哪些收获?同学们再见!
