北师大版数学九年级下册 第一章 直角三角形的边角关系 锐角三角函数(一)课件(共19张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 第一章 直角三角形的边角关系 锐角三角函数(一)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 693.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 13:43:41 | ||
图片预览




文档简介
(共19张PPT)
第1课时 锐角三角函数(一)
第一章 直角三角形的边角关系
目录
01
温故知新
02
知识重点
03
对点范例
04
典型例题
05
举一反三
06
创新设计
1.若一个直角三角形两直角边的比是3∶4,斜边长为20,则这个三角形的较短直角边的长是( )
A.12 B.16 C.20 D.15
温故知新 (限时3分钟)
A
D
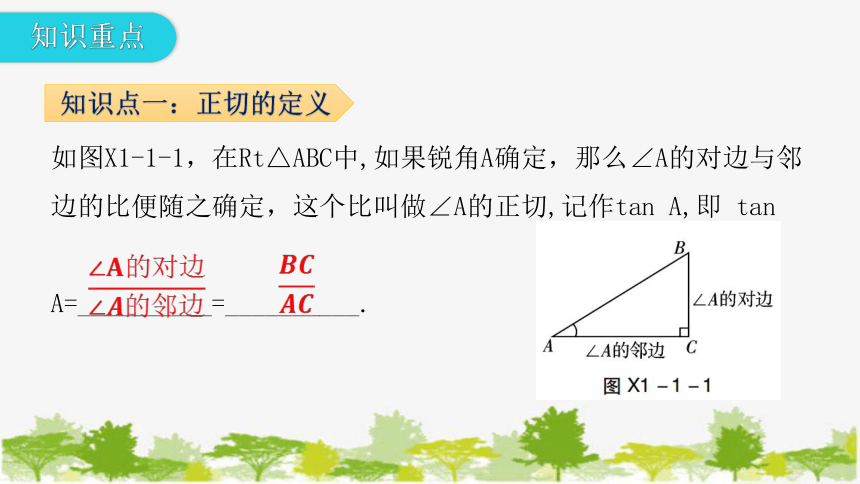
知识点一:正切的定义
知识重点
如图X1-1-1,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tan A,即 tan
A=__________=__________.
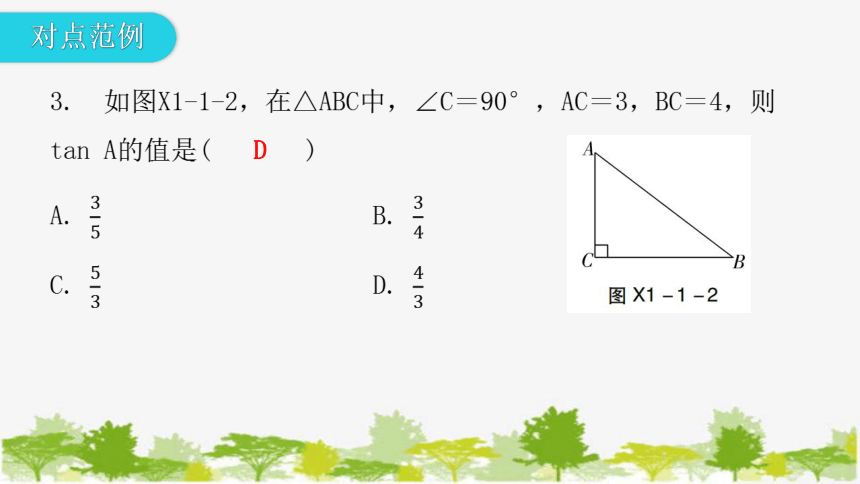
对点范例
D
知识点二:坡度
知识重点
坡面的____________高度与____________宽度的比称为坡度(或坡比).
铅直
水平
对点范例
C
典型例题
【例1】(课本P4随堂练习)如图X1-1-3,△ABC是等腰三角形,你能根据图中所给数据求出tan C吗?
思路点拨:先根据等腰三角形的三线合一求出CD的长,再根据锐角三角函数的定义求出tan C.
举一反三
5. 如图X1-1-4,在等腰三角形ABC中,请根据图中所给数据求出tan B.
典型例题
思路点拨:先根据直角三角形的边角关系求出AC,再根据勾股定理求出AB.
举一反三
6. 如图X1-1-6,在△ABC中,AB=10 cm,BC=9 cm,△ABC的面积为27 cm2.求tan B的值.
创新设计
谢 谢
第1课时 锐角三角函数(一)
第一章 直角三角形的边角关系
目录
01
温故知新
02
知识重点
03
对点范例
04
典型例题
05
举一反三
06
创新设计
1.若一个直角三角形两直角边的比是3∶4,斜边长为20,则这个三角形的较短直角边的长是( )
A.12 B.16 C.20 D.15
温故知新 (限时3分钟)
A
D
知识点一:正切的定义
知识重点
如图X1-1-1,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tan A,即 tan
A=__________=__________.
对点范例
D
知识点二:坡度
知识重点
坡面的____________高度与____________宽度的比称为坡度(或坡比).
铅直
水平
对点范例
C
典型例题
【例1】(课本P4随堂练习)如图X1-1-3,△ABC是等腰三角形,你能根据图中所给数据求出tan C吗?
思路点拨:先根据等腰三角形的三线合一求出CD的长,再根据锐角三角函数的定义求出tan C.
举一反三
5. 如图X1-1-4,在等腰三角形ABC中,请根据图中所给数据求出tan B.
典型例题
思路点拨:先根据直角三角形的边角关系求出AC,再根据勾股定理求出AB.
举一反三
6. 如图X1-1-6,在△ABC中,AB=10 cm,BC=9 cm,△ABC的面积为27 cm2.求tan B的值.
创新设计
谢 谢
