探索图形(课件)-五年级下册数学人教版(共22张PPT)
文档属性
| 名称 | 探索图形(课件)-五年级下册数学人教版(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 14:25:56 | ||
图片预览



文档简介
(共22张PPT)
人教版五年级年级下册数学
探 索 图 形
6个面:每个面面积相等
12条棱:每条棱长度相等
8个顶点
正方体的面、棱、顶点各有什么特征?
1cm
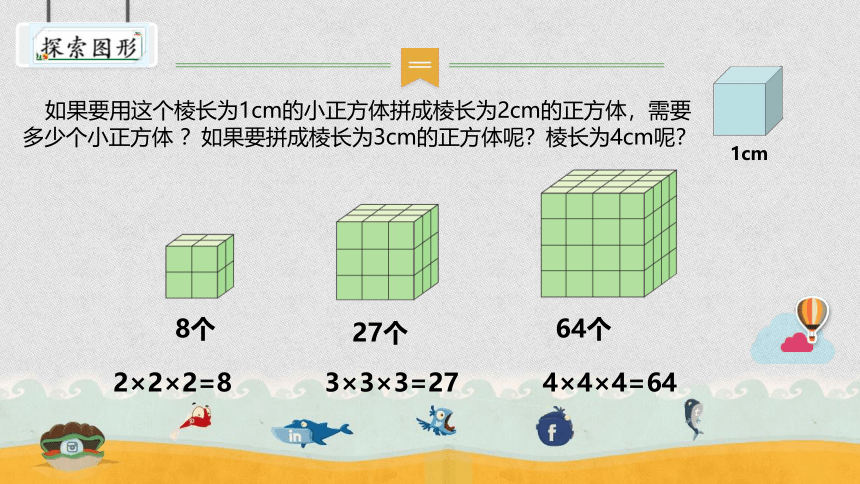
如果要用这个棱长为1cm的小正方体拼成棱长为2cm的正方体,需要多少个小正方体 ?如果要拼成棱长为3cm的正方体呢?棱长为4cm呢?
8个
2×2×2=8
27个
3×3×3=27
64个
4×4×4=64
①
②
③
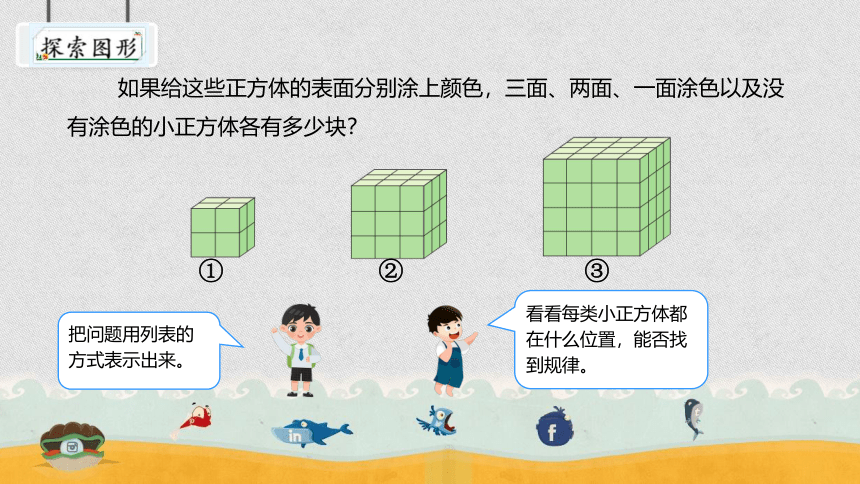
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
如果给这些正方体的表面分别涂上颜色,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
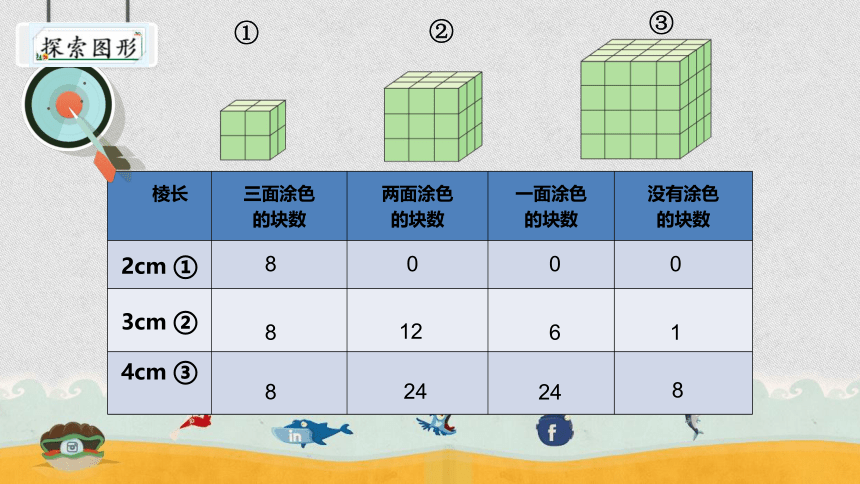
棱长 三面涂色 的块数 两面涂色 的块数 一面涂色 的块数 没有涂色
的块数
2cm ①
3cm ②
4cm ③
8
8
8
0
12
24
0
0
6
1
24
8
棱长 三面涂色 的块数 两面涂色 的块数 一面涂色 的块数 没有涂色
的块数
8 0 0 0
8 12 6 1
8 24
24
8
8
36
54
27
8
48
96
64
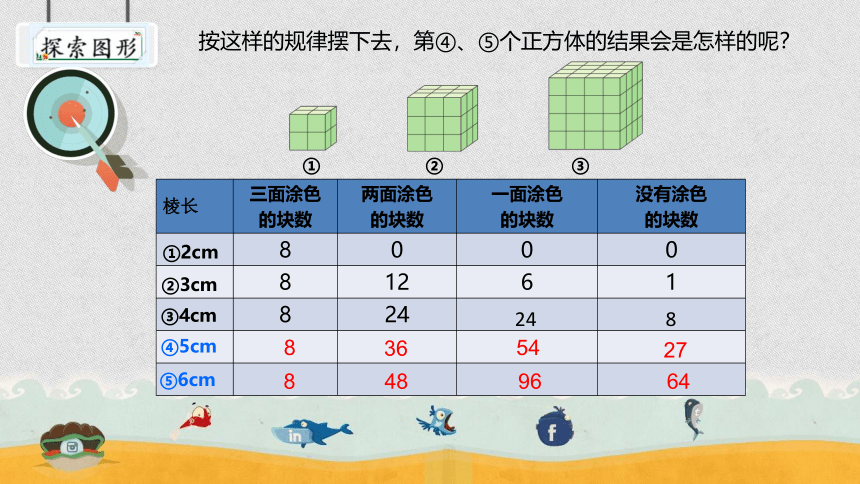
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
①
②
③
①2cm
②3cm
③4cm
④5cm
⑤6cm
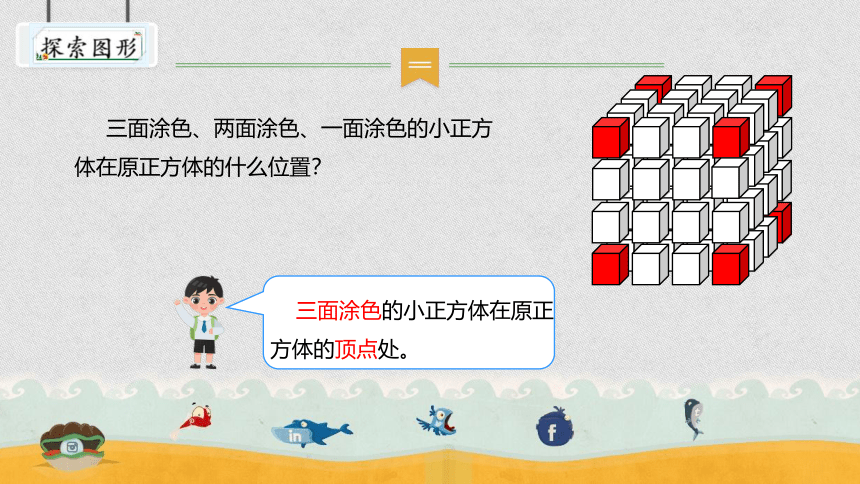
三面涂色的小正方体在原正方体的顶点处。
三面涂色、两面涂色、一面涂色的小正方体在原正方体的什么位置?
两面涂色的小正方体在原正方体棱上除去两端的位置。
一面涂色的小正方体在原正方体每个面除去周边一圈的位置。
观察填出的表格,你能发现什么规律?
棱长 3面涂色 块数 2面涂色 块数 1面涂色 块数 没有涂色块数
①2cm 8 0 0 0
②3cm 8 12 6 1
③4cm 8 24 24 8
④5cm 8 36 54 27
⑤6cm 8 48 96 64
棱长 3面涂色 块数 2面涂色 块数 1面涂色 块数 没有涂色块数
①2cm 8 0 0 0
②3cm 8 12 6 1
③4cm 8 24 24 8
④5cm 8 36 54 27
⑤6cm 8 48 96 64
12条棱有 个
2面涂色的小正方体。
(n-2)
×12
每条棱有 个
2面涂色的小正方体。
n-2
棱长是n厘米时,棱被平均分成了n份
棱长 3面涂色 块数 2面涂色 块数 1面涂色 块数 没有涂色块数
①2cm 8 0 0 0
②3cm 8 12 6 1
③4cm 8 24 24 8
④5cm 8 36 54 27
⑤6cm 8 48 96 64
3×3
2×2
1×1
棱长是n厘米时,棱被平均分成了n份
每个面有 个1面涂色的小正方体。
(n-2)2
6个面有 个1面涂色的小正方体。
(n-2)2×6
没有涂色的小正方体有着怎样的规律呢?
棱长 3 4 5
没有涂色的个数
33
23
13
33=27
23=8
13=1
1
8
27
当棱长n厘米时,棱被平均分成n份
当棱长为n厘米时,没有涂色的小正方体有 个
(n-2)3
8+96+384=488(个)<512个
所以老师赢的可能性大。
小正方体表面涂色的规律
n
8
12(n-2)
6(n-2)2
当n =10时,3面涂色的小正方体有____个,
2面涂色的小正方体有____个,
1面涂色的小正方体有____个,
各面无涂色的小正方体有____个。
8
96
384
512
( n-2)3
棱长 3面涂色的个数 2面涂色的个数 1面涂色的个数 没有涂色的个数
游戏:
把表面涂色的正方体每条棱平均分成10份,从切成的小正方体中任取一个,若3面涂色、2面涂色、1面涂色时,同学赢;否则,老师赢。你认为谁赢得可能性大一些?为什么?
一个正方体,在它的每个面上都涂上红色。再把它切成棱长是1厘米的小正方体。已知两面涂色的小正方体有48个,大正方体的棱长是几厘米?
48÷12=4(个)
4+2=6(个)
1×6=6(厘米)
答:大正方体的棱长是6厘米。
如果摆成下面的几何体,你会数吗?
4
10
20
同学们,这节课你学到了什么呢?
把长、宽、高分别为a厘米、b厘米、h厘米(均大于2) 的表面涂色的长方体切割成棱长为1厘米的小正方体,如何计算小正方体的总数、涂色面数不同的小正方体个数呢?
a厘米
b厘米
h厘米
课后思考:
人教版五年级年级下册数学
探 索 图 形
6个面:每个面面积相等
12条棱:每条棱长度相等
8个顶点
正方体的面、棱、顶点各有什么特征?
1cm
如果要用这个棱长为1cm的小正方体拼成棱长为2cm的正方体,需要多少个小正方体 ?如果要拼成棱长为3cm的正方体呢?棱长为4cm呢?
8个
2×2×2=8
27个
3×3×3=27
64个
4×4×4=64
①
②
③
把问题用列表的方式表示出来。
看看每类小正方体都在什么位置,能否找到规律。
如果给这些正方体的表面分别涂上颜色,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
棱长 三面涂色 的块数 两面涂色 的块数 一面涂色 的块数 没有涂色
的块数
2cm ①
3cm ②
4cm ③
8
8
8
0
12
24
0
0
6
1
24
8
棱长 三面涂色 的块数 两面涂色 的块数 一面涂色 的块数 没有涂色
的块数
8 0 0 0
8 12 6 1
8 24
24
8
8
36
54
27
8
48
96
64
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
①
②
③
①2cm
②3cm
③4cm
④5cm
⑤6cm
三面涂色的小正方体在原正方体的顶点处。
三面涂色、两面涂色、一面涂色的小正方体在原正方体的什么位置?
两面涂色的小正方体在原正方体棱上除去两端的位置。
一面涂色的小正方体在原正方体每个面除去周边一圈的位置。
观察填出的表格,你能发现什么规律?
棱长 3面涂色 块数 2面涂色 块数 1面涂色 块数 没有涂色块数
①2cm 8 0 0 0
②3cm 8 12 6 1
③4cm 8 24 24 8
④5cm 8 36 54 27
⑤6cm 8 48 96 64
棱长 3面涂色 块数 2面涂色 块数 1面涂色 块数 没有涂色块数
①2cm 8 0 0 0
②3cm 8 12 6 1
③4cm 8 24 24 8
④5cm 8 36 54 27
⑤6cm 8 48 96 64
12条棱有 个
2面涂色的小正方体。
(n-2)
×12
每条棱有 个
2面涂色的小正方体。
n-2
棱长是n厘米时,棱被平均分成了n份
棱长 3面涂色 块数 2面涂色 块数 1面涂色 块数 没有涂色块数
①2cm 8 0 0 0
②3cm 8 12 6 1
③4cm 8 24 24 8
④5cm 8 36 54 27
⑤6cm 8 48 96 64
3×3
2×2
1×1
棱长是n厘米时,棱被平均分成了n份
每个面有 个1面涂色的小正方体。
(n-2)2
6个面有 个1面涂色的小正方体。
(n-2)2×6
没有涂色的小正方体有着怎样的规律呢?
棱长 3 4 5
没有涂色的个数
33
23
13
33=27
23=8
13=1
1
8
27
当棱长n厘米时,棱被平均分成n份
当棱长为n厘米时,没有涂色的小正方体有 个
(n-2)3
8+96+384=488(个)<512个
所以老师赢的可能性大。
小正方体表面涂色的规律
n
8
12(n-2)
6(n-2)2
当n =10时,3面涂色的小正方体有____个,
2面涂色的小正方体有____个,
1面涂色的小正方体有____个,
各面无涂色的小正方体有____个。
8
96
384
512
( n-2)3
棱长 3面涂色的个数 2面涂色的个数 1面涂色的个数 没有涂色的个数
游戏:
把表面涂色的正方体每条棱平均分成10份,从切成的小正方体中任取一个,若3面涂色、2面涂色、1面涂色时,同学赢;否则,老师赢。你认为谁赢得可能性大一些?为什么?
一个正方体,在它的每个面上都涂上红色。再把它切成棱长是1厘米的小正方体。已知两面涂色的小正方体有48个,大正方体的棱长是几厘米?
48÷12=4(个)
4+2=6(个)
1×6=6(厘米)
答:大正方体的棱长是6厘米。
如果摆成下面的几何体,你会数吗?
4
10
20
同学们,这节课你学到了什么呢?
把长、宽、高分别为a厘米、b厘米、h厘米(均大于2) 的表面涂色的长方体切割成棱长为1厘米的小正方体,如何计算小正方体的总数、涂色面数不同的小正方体个数呢?
a厘米
b厘米
h厘米
课后思考:
