15.3 等腰三角形(1)课件
图片预览

文档简介
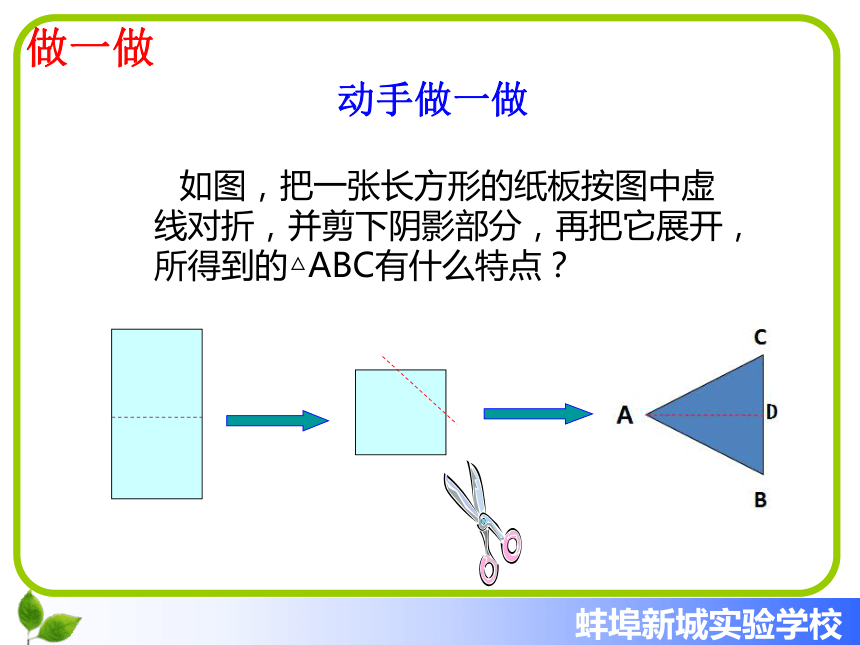
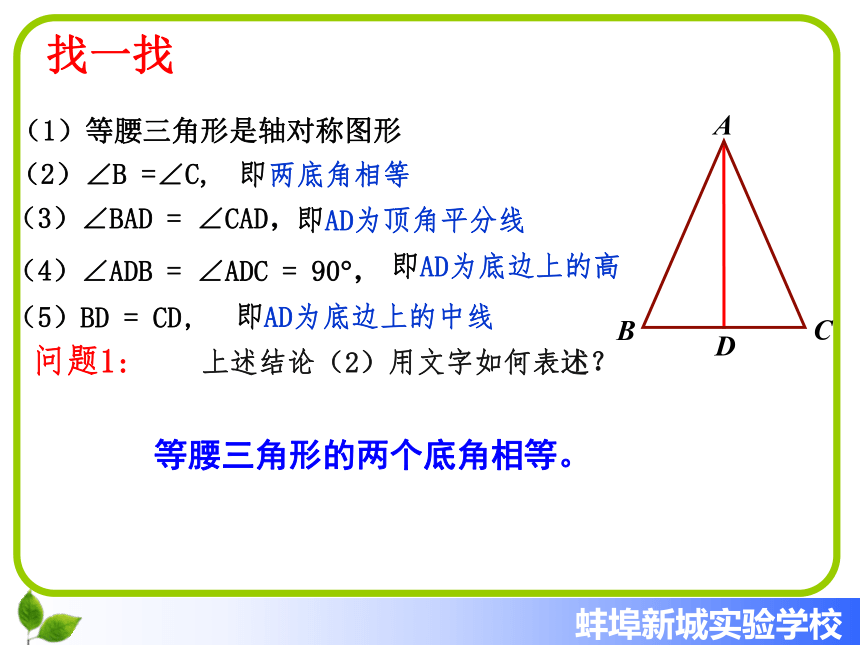
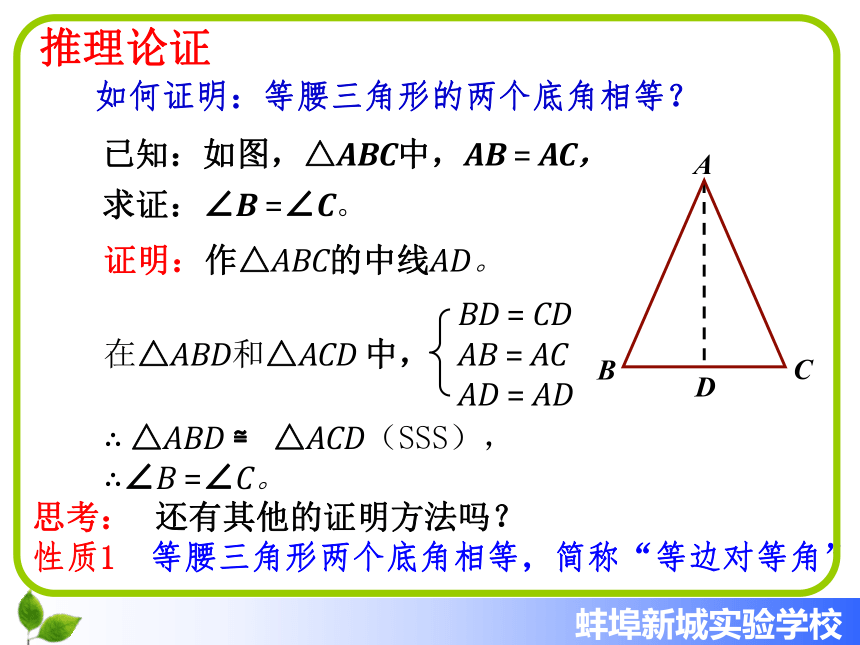
课件13张PPT。(第一课时)15.3等腰三角形想一想问题 校门上的显示屏水平了吗? 学校大门上安装电子显示屏的时候,负责安装的工人师傅忘记带测水平的工具,为了检查显示屏是否水平,数学老师门老师从办公室找来一把等腰直角三角尺,在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在显示屏上,如果线绳经过三角尺的直角顶点,就确信显示屏是水平的,同学们知道这样做的道理吗?动手做一做做一做 如图,把一张长方形的纸板按图中虚线对折,并剪下阴影部分,再把它展开,所得到的△ABC有什么特点?(1)等腰三角形是轴对称图形(2)∠B =∠C,(5)BD = CD,(4)∠ADB = ∠ADC = 90?,(3)∠BAD = ∠CAD,问题1: 上述结论(2)用文字如何表述?等腰三角形的两个底角相等。即两底角相等即AD为底边上的中线即AD为底边上的高即AD为顶角平分线找一找如何证明:等腰三角形的两个底角相等?已知:如图,△ABC中,AB = AC,求证:∠B =∠C。思考: 还有其他的证明方法吗?DBCA推理论证性质1 等腰三角形两个底角相等,简称“等边对等角”。⒈等腰三角形一个底角为40°,它的顶角为______.2.等腰三角形一个角为40°,它的另外两个角为
. 100°100°、40 °或70 °、70 ° 3.等腰三角形一个角为120°,它的另外两个角
为 . 30°、30°练一练60°4.在△ABC中,若AB=BC=CA,则 ∠A=∠B=∠C= .推论:等边三角形三个内角都相等,
每一个角都等于60°.(1)等腰三角形是轴对称图形(2)∠B =∠C,(5)BD = CD,(4)∠ADB = ∠ADC = 90?,(3)∠BAD = ∠CAD,问题2: 已知等腰三角形ABC中,如果已知结论(3)成立,
能够得到结论(4)和(5)成立吗? 性质2:等腰三角形顶角的平分线垂直平分底边。即两底角相等即AD为底边上的中线即AD为底边上的高即AD为顶角平分线想一想① ∵ AD⊥BC,
∴ ∠____ = ∠____, ___= ___ 。 ② ∵AD是中线,∴ ⊥ ,∠ =∠ 。③ ∵AD是角平分线,∴ ⊥ , = 。BAD CAD BD CD AD BC AD BCBAD CADBD CD 在△ABC中,当AB = AC 时, 推论:等腰三角形顶角的平分线、底边上的高和底边上
的中线互相重合。(简称“三线合一”)探索新知(三线合一)想一想问题 校门上的显示屏水平了吗? 学校大门上安装电子显示屏的时候,负责安装的工人师傅忘记带测水平的工具,为了检查显示屏是否水平,数学老师门老师从办公室找来一把等腰直角三角尺,在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在显示屏上,如果线绳经过三角尺的直角顶点,就确信显示屏是水平的,同学们知道这样做的道理吗?
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,求∠DAE的度数.又∵BD=AD(已知)
∴∠1=∠B= 30°(等边对等角) 同理 ∠2 =∠C= 30°.
∴∠DAE =∠BAC-∠1-∠2
=120°-30°-30°
=60 °.
AB=AC,变式练习: 如图在△ABC中, ∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,求∠DAE的度数.练一练
学习小结小结梳理:本节课我学习了……布置作业:必做题:习题16.3 1、2
选做题:已知,如图AB=AC,AD=AE.
求证:BD=CE.
. 100°100°、40 °或70 °、70 ° 3.等腰三角形一个角为120°,它的另外两个角
为 . 30°、30°练一练60°4.在△ABC中,若AB=BC=CA,则 ∠A=∠B=∠C= .推论:等边三角形三个内角都相等,
每一个角都等于60°.(1)等腰三角形是轴对称图形(2)∠B =∠C,(5)BD = CD,(4)∠ADB = ∠ADC = 90?,(3)∠BAD = ∠CAD,问题2: 已知等腰三角形ABC中,如果已知结论(3)成立,
能够得到结论(4)和(5)成立吗? 性质2:等腰三角形顶角的平分线垂直平分底边。即两底角相等即AD为底边上的中线即AD为底边上的高即AD为顶角平分线想一想① ∵ AD⊥BC,
∴ ∠____ = ∠____, ___= ___ 。 ② ∵AD是中线,∴ ⊥ ,∠ =∠ 。③ ∵AD是角平分线,∴ ⊥ , = 。BAD CAD BD CD AD BC AD BCBAD CADBD CD 在△ABC中,当AB = AC 时, 推论:等腰三角形顶角的平分线、底边上的高和底边上
的中线互相重合。(简称“三线合一”)探索新知(三线合一)想一想问题 校门上的显示屏水平了吗? 学校大门上安装电子显示屏的时候,负责安装的工人师傅忘记带测水平的工具,为了检查显示屏是否水平,数学老师门老师从办公室找来一把等腰直角三角尺,在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端挂一个铅锤,把这块三角尺的斜边贴在显示屏上,如果线绳经过三角尺的直角顶点,就确信显示屏是水平的,同学们知道这样做的道理吗?
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,求∠DAE的度数.又∵BD=AD(已知)
∴∠1=∠B= 30°(等边对等角) 同理 ∠2 =∠C= 30°.
∴∠DAE =∠BAC-∠1-∠2
=120°-30°-30°
=60 °.
AB=AC,变式练习: 如图在△ABC中, ∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,求∠DAE的度数.练一练
学习小结小结梳理:本节课我学习了……布置作业:必做题:习题16.3 1、2
选做题:已知,如图AB=AC,AD=AE.
求证:BD=CE.
