平行四边形性质2[下学期]
文档属性
| 名称 | 平行四边形性质2[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 76.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-19 00:00:00 | ||
图片预览

文档简介
课件19张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
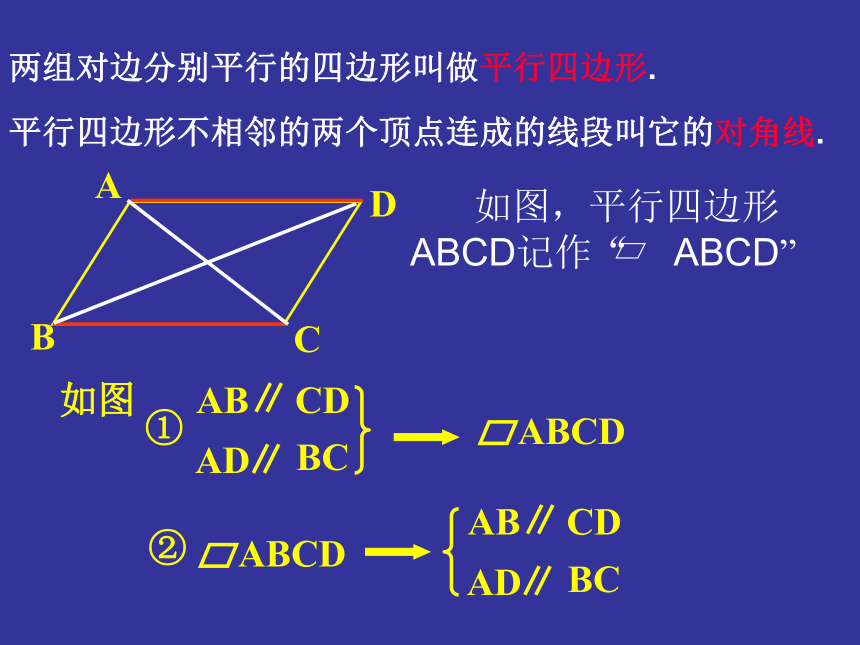
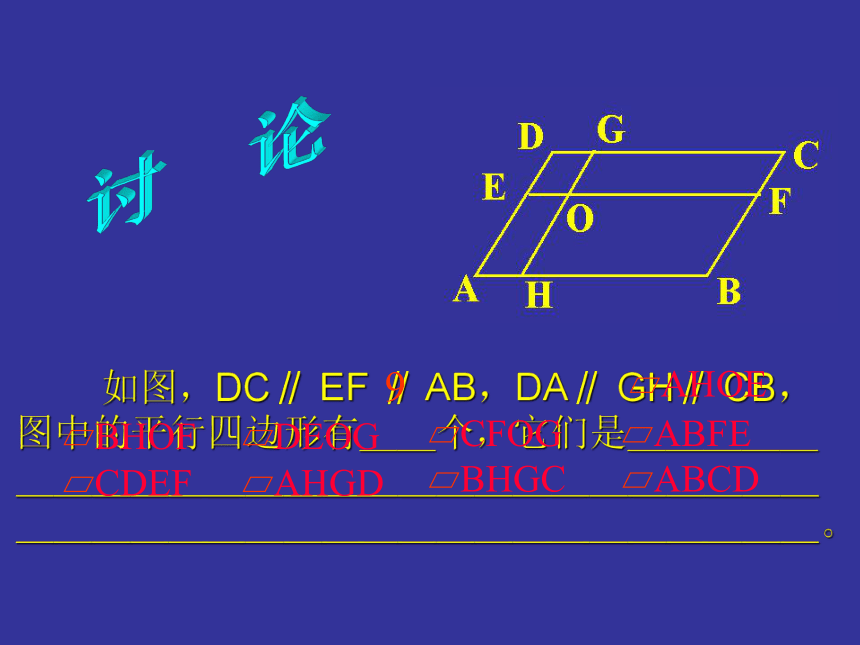
两组对边分别平行的四边形叫做平行四边形.平行四边形不相邻的两个顶点连成的线段叫它的对角线. 如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。讨 论9 平行四边形的对边相等
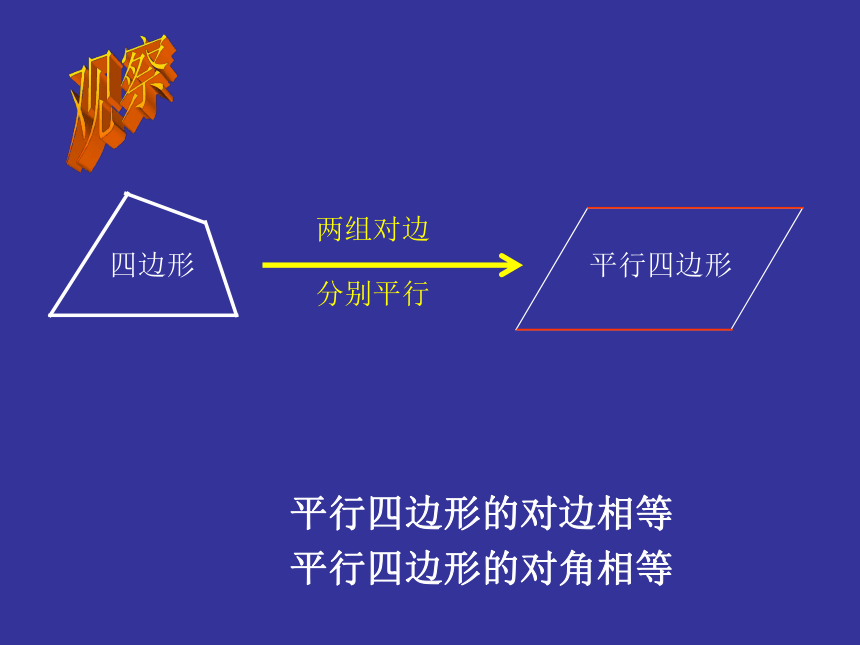
平行四边形的对角相等观察 平行四边形:
两组对边分别相等
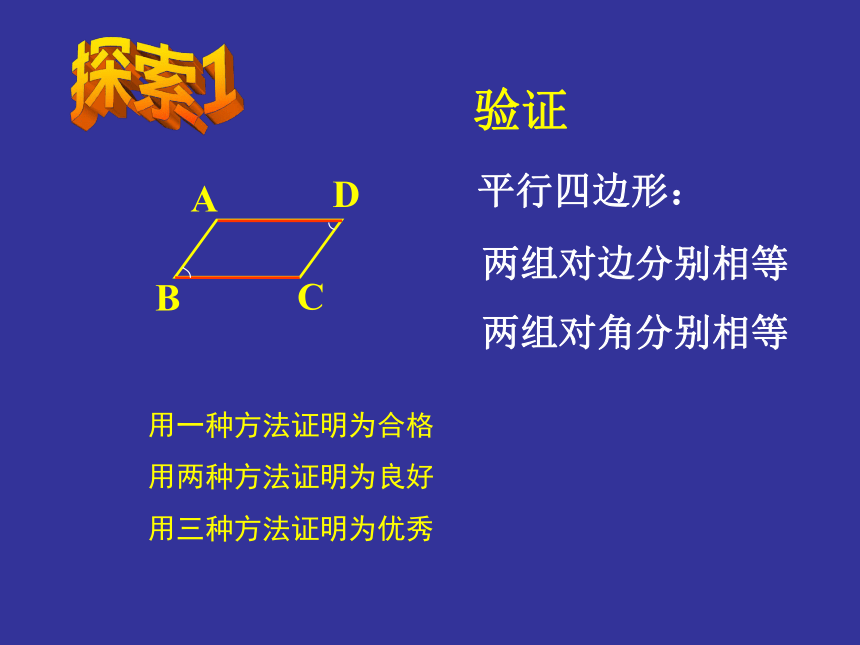
两组对角分别相等 探索1验证用一种方法证明为合格
用两种方法证明为良好
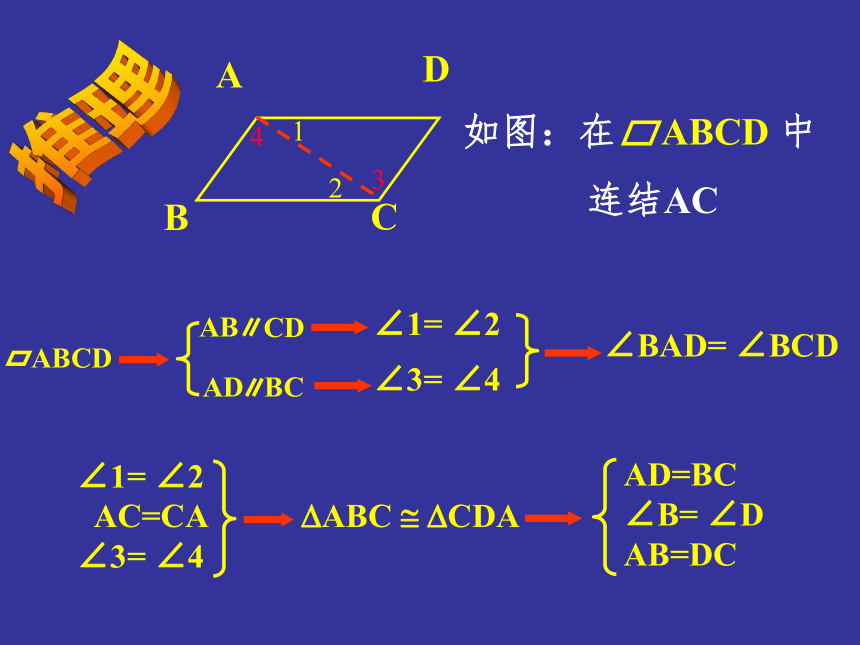
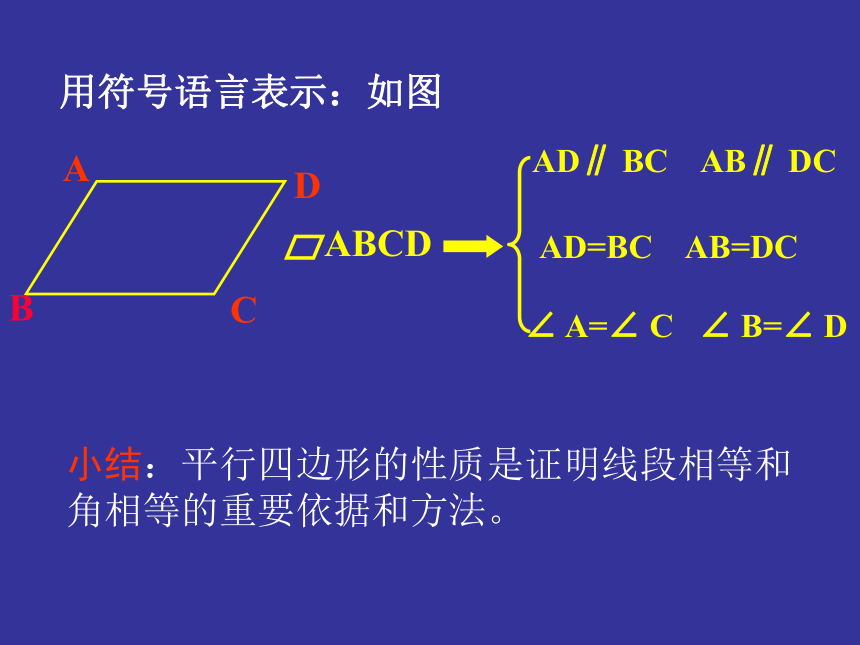
用三种方法证明为优秀推理∠1= ∠2∠3= ∠4∠BAD= ∠BCD用符号语言表示:如图小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? ADBC解:
∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m试一试50°130°100 2.已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF
求证:AF=CEABDCFE 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。2ABCD∵∠1=∠2 ∴AD∥BC
同理:AB∥DC ∴四边形ABCD是平行四边形1 在纸上画□ABCD,将它剪下.再在一张纸上沿□ABCD的边缘画出一个与□ABCD相同的□EFGH.在它们的中心O(两条对角线的交点)钉一个图钉.将□ABCD绕点O旋转180°,它还和□EFGH重合吗?你能从中看出前面得到的□ABCD的边角关系吗?
进一步的,你能发现OA与OC、OB与OD的关系吗?探索2 定理:平行四边形的对角线互相平分. 如图四边形ABCD是□,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及□ ABCD的面积.ABCDO 上图的平行四边形ABCD中有几对全等三角形? 议一议 例1.如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM练一练例2.已知:如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,BE平分∠ABC交AD于E,交CD的延长线于F.
⑴△ABE与△DFE全等吗?⑵求CF的长.⑶若连结CE,则CE与BE有怎样的位置关系?⑷能否求出CE的长?小结1.平行四边形的概念
2.平行四边形的性质
3.解决平行四边形的有关问题经常连结
对角线转化为三角形。作业1.开放作业:将本节课提出的尚未解决的问题作为课后作业。
2.规范作业 : 教材 99页 1、2、3题,作业本1再 见
——毕达哥拉斯
两组对边分别平行的四边形叫做平行四边形.平行四边形不相邻的两个顶点连成的线段叫它的对角线. 如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________。讨 论9 平行四边形的对边相等
平行四边形的对角相等观察 平行四边形:
两组对边分别相等
两组对角分别相等 探索1验证用一种方法证明为合格
用两种方法证明为良好
用三种方法证明为优秀推理∠1= ∠2∠3= ∠4∠BAD= ∠BCD用符号语言表示:如图小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。例1 如图 小明用一根36m长的绳子围成了一个 平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? ADBC解:
∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m试一试50°130°100 2.已知 ABCD,延长AB到E, 延长CD到F ,使BE=DF
求证:AF=CEABDCFE 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。2ABCD∵∠1=∠2 ∴AD∥BC
同理:AB∥DC ∴四边形ABCD是平行四边形1 在纸上画□ABCD,将它剪下.再在一张纸上沿□ABCD的边缘画出一个与□ABCD相同的□EFGH.在它们的中心O(两条对角线的交点)钉一个图钉.将□ABCD绕点O旋转180°,它还和□EFGH重合吗?你能从中看出前面得到的□ABCD的边角关系吗?
进一步的,你能发现OA与OC、OB与OD的关系吗?探索2 定理:平行四边形的对角线互相平分. 如图四边形ABCD是□,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及□ ABCD的面积.ABCDO 上图的平行四边形ABCD中有几对全等三角形? 议一议 例1.如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BA
∴∠BAD=∠CAD
∵AB//EF
∴ ∠BAD=∠AEF
∴∠CAD =∠AEF
∴ AF=EF
∴ AF=BM练一练例2.已知:如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,BE平分∠ABC交AD于E,交CD的延长线于F.
⑴△ABE与△DFE全等吗?⑵求CF的长.⑶若连结CE,则CE与BE有怎样的位置关系?⑷能否求出CE的长?小结1.平行四边形的概念
2.平行四边形的性质
3.解决平行四边形的有关问题经常连结
对角线转化为三角形。作业1.开放作业:将本节课提出的尚未解决的问题作为课后作业。
2.规范作业 : 教材 99页 1、2、3题,作业本1再 见
