19.1.2平行四边形的判定(2)[下学期]
文档属性
| 名称 | 19.1.2平行四边形的判定(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 849.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-20 21:07:00 | ||
图片预览



文档简介
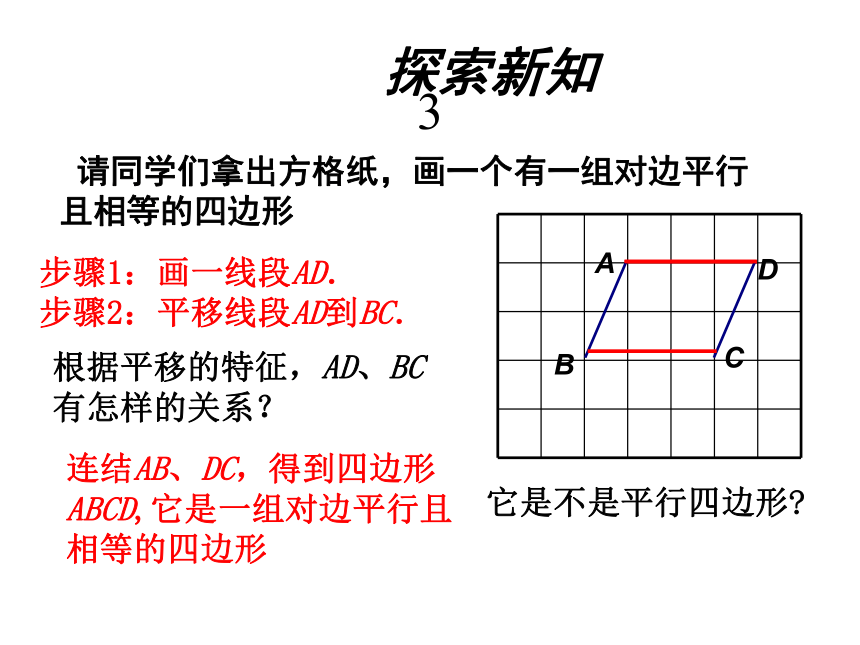
课件18张PPT。19.1.2平行四边形的判定(2)? 探索新知 请同学们拿出方格纸,画一个有一组对边平行且相等的四边形 步骤1:画一线段AD.
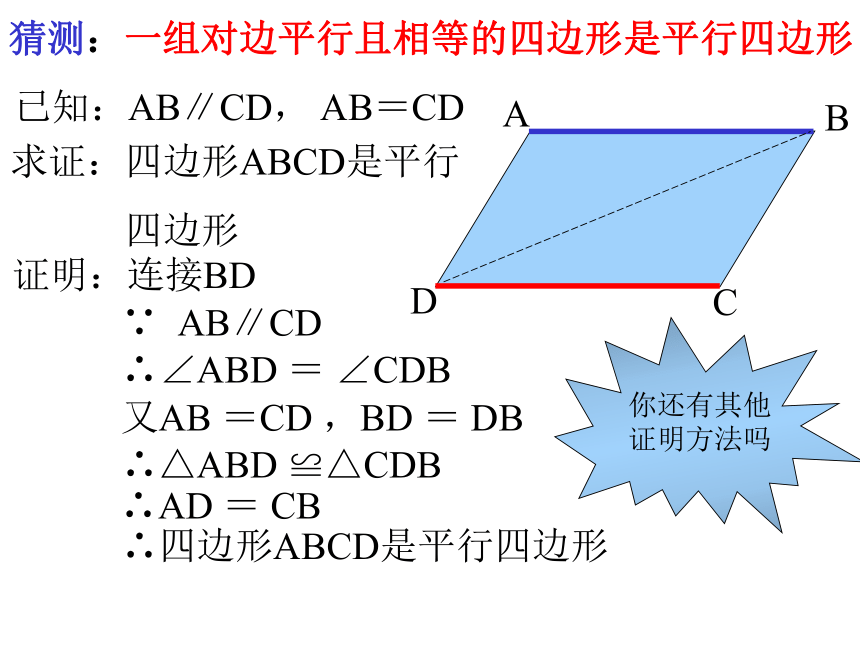
步骤2:平移线段AD到BC.根据平移的特征,AD、BC有怎样的关系? 连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形它是不是平行四边形?CBDA3猜测:一组对边平行且相等的四边形是平行四边形已知:AB∥CD, AB=CD求证:四边形ABCD是平行
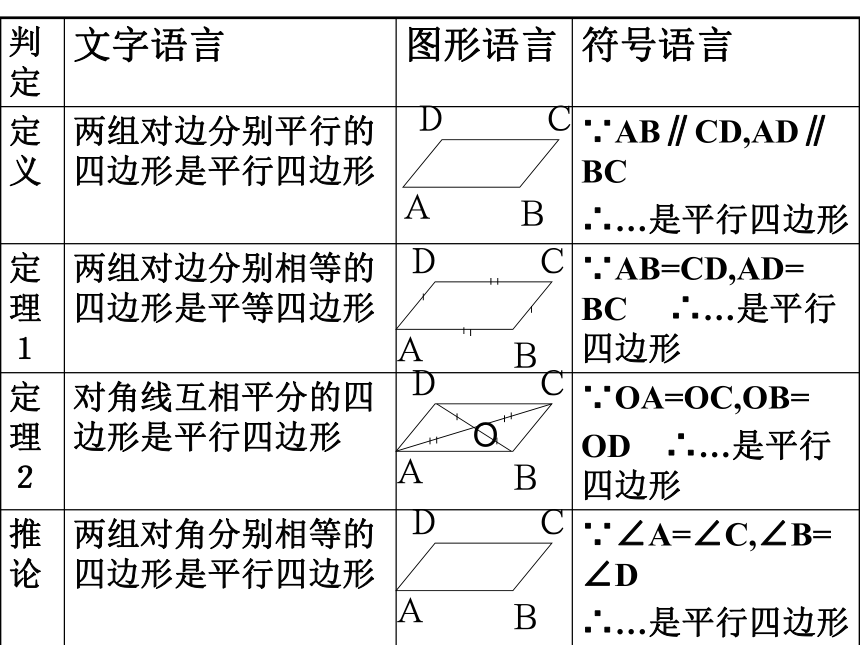
四边形证明:连接BD判定方法(4)一组对边平行且相等(记作:“ ”)
的四边形是平行四边形∥=? 探索新知一组对边平行且相等的四边形是平行四边形 ∵AB∥CD,AB = DC,
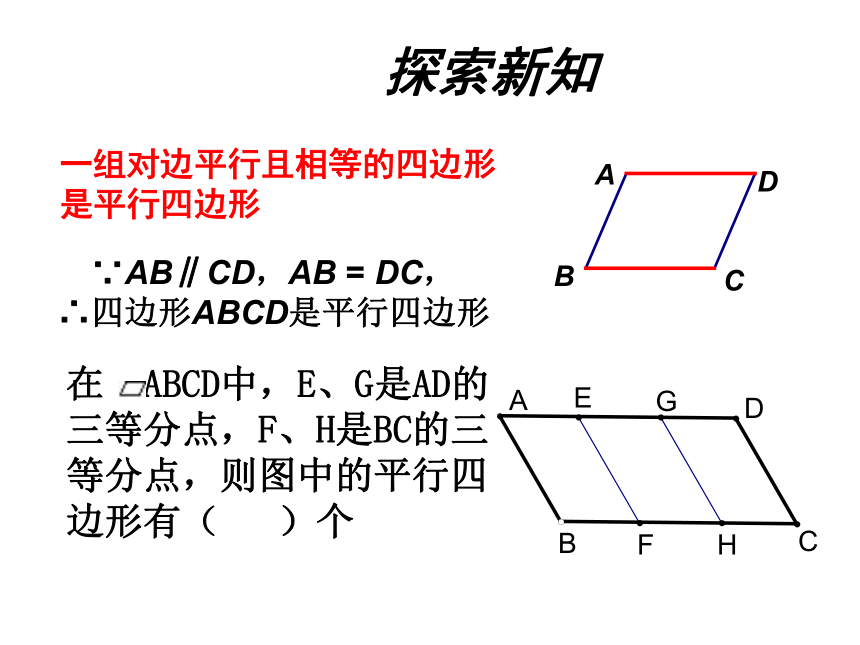
∴四边形ABCD是平行四边形 CBDA在 ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有( )个 两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行一组对边平行且相等四边形是平行四边形边角对角线:平行四边形的判定方法共有几种?3. 生物实验室有一块平行四边形的玻璃片,在做实验时,小明 一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想:(请用尺规完成) BACD实践应用 例1:如图,在 ABCD中,已知点E和点F分别
在AD和BC上,且AE=CF,连结CE和AF,
试说明四边形AFCE是平行四边形。 把条件换成BF=ED呢? OOE=OF吗? 练一练:1、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形 2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180D5、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D 如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO小结:1、你到今天为止共学到了几种判定平行四边形的方法?
2、你能够灵活运用吗?
四边形两组对边分别平行对角线互相平分一组对边平行且相等平行四边形两组对边分别相等两组对角分别相等
步骤2:平移线段AD到BC.根据平移的特征,AD、BC有怎样的关系? 连结AB、DC,得到四边形ABCD,它是一组对边平行且相等的四边形它是不是平行四边形?CBDA3猜测:一组对边平行且相等的四边形是平行四边形已知:AB∥CD, AB=CD求证:四边形ABCD是平行
四边形证明:连接BD判定方法(4)一组对边平行且相等(记作:“ ”)
的四边形是平行四边形∥=? 探索新知一组对边平行且相等的四边形是平行四边形 ∵AB∥CD,AB = DC,
∴四边形ABCD是平行四边形 CBDA在 ABCD中,E、G是AD的三等分点,F、H是BC的三等分点,则图中的平行四边形有( )个 两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行一组对边平行且相等四边形是平行四边形边角对角线:平行四边形的判定方法共有几种?3. 生物实验室有一块平行四边形的玻璃片,在做实验时,小明 一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想:(请用尺规完成) BACD实践应用 例1:如图,在 ABCD中,已知点E和点F分别
在AD和BC上,且AE=CF,连结CE和AF,
试说明四边形AFCE是平行四边形。 把条件换成BF=ED呢? OOE=OF吗? 练一练:1、已知在平行四边形ABCD中,E、G分别在AB、CD上,H、F在对角线上,且AE=CG ,AH=CF, 求证:四边形EFGH为平行四边形 2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180D5、下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D 如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO小结:1、你到今天为止共学到了几种判定平行四边形的方法?
2、你能够灵活运用吗?
四边形两组对边分别平行对角线互相平分一组对边平行且相等平行四边形两组对边分别相等两组对角分别相等
