鲁教版(五四制)数学八年级上册 4.2 图形的旋转-第三课时 课件(共17张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 4.2 图形的旋转-第三课时 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 362.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
第三课时
图形的旋转
Contents
目录
01
02
03
04
学习目标
合作探究
布置作业
05
旧知回顾
拓展练习
利用旋转的性质解决比较综合的问题。
︵
︵
F
A
B
C
D
E
O
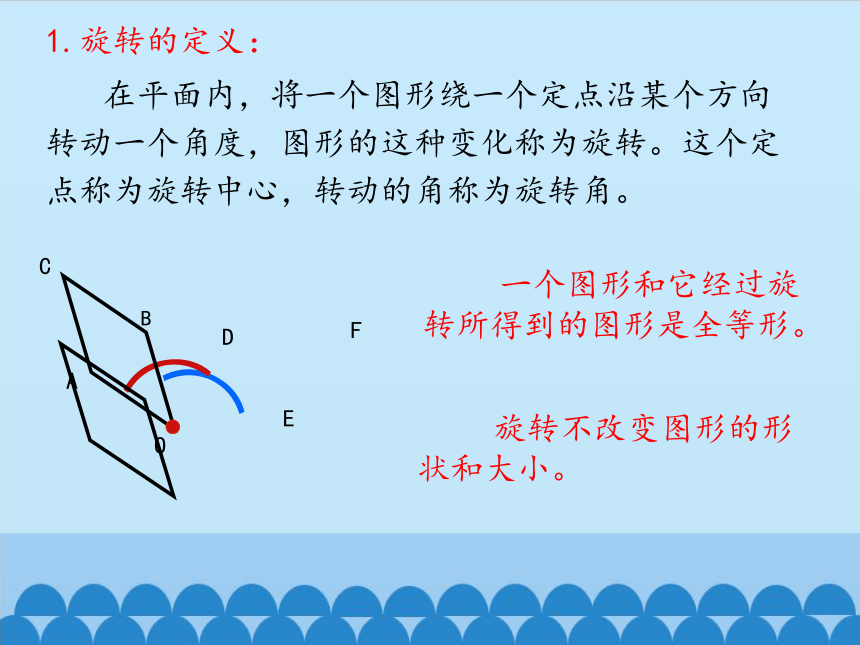
旋转不改变图形的形状和大小。
1.旋转的定义:
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,图形的这种变化称为旋转。这个定点称为旋转中心,转动的角称为旋转角。
一个图形和它经过旋转所得到的图形是全等形。
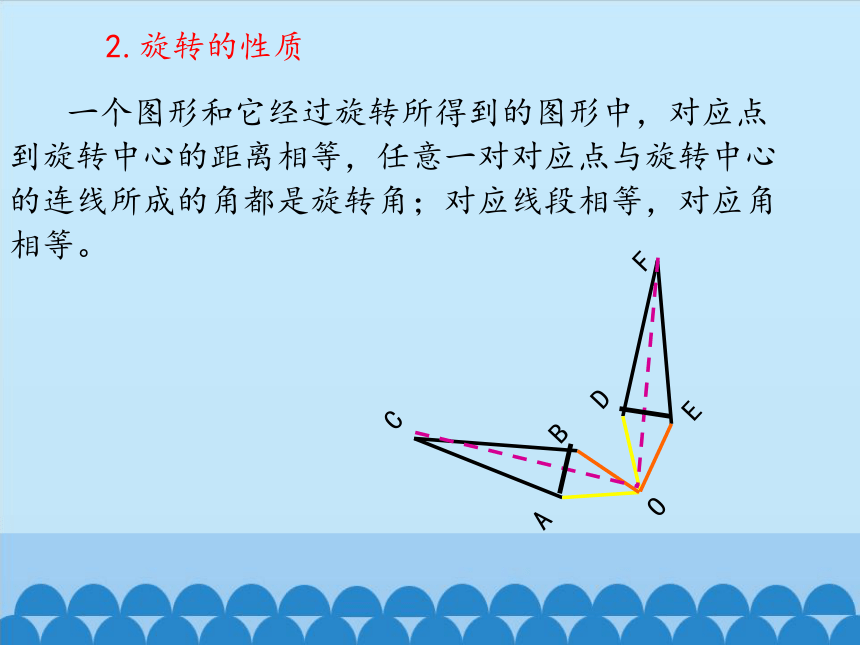
一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,任意一对对应点与旋转中心的连线所成的角都是旋转角;对应线段相等,对应角相等。
2.旋转的性质
A
O
C
D
F
E
B
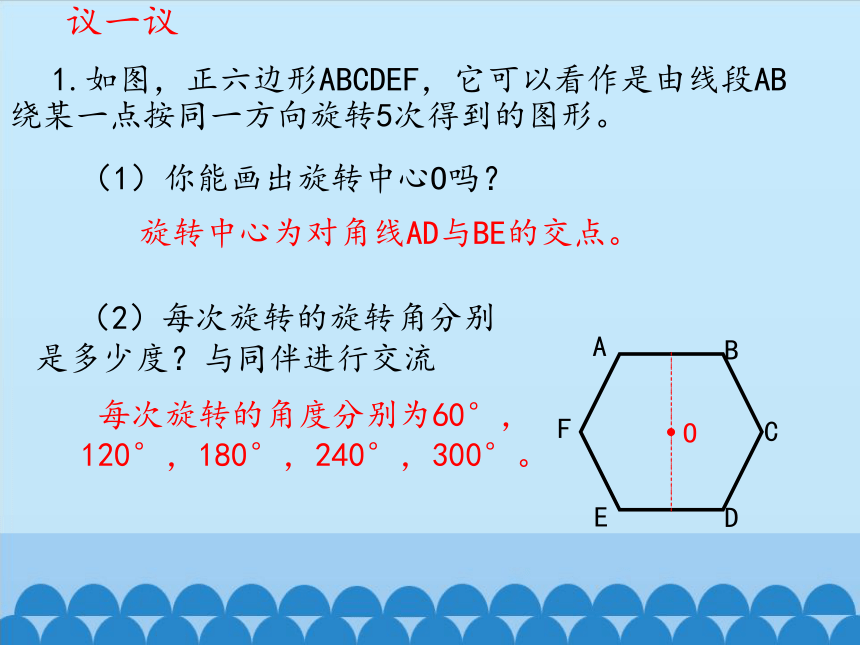
1.如图,正六边形ABCDEF,它可以看作是由线段AB绕某一点按同一方向旋转5次得到的图形。
议一议
(1)你能画出旋转中心O吗?
(2)每次旋转的旋转角分别是多少度?与同伴进行交流
B
F
A
E
D
C
旋转中心为对角线AD与BE的交点。
O
每次旋转的角度分别为60°,120°,180°,240°,300°。
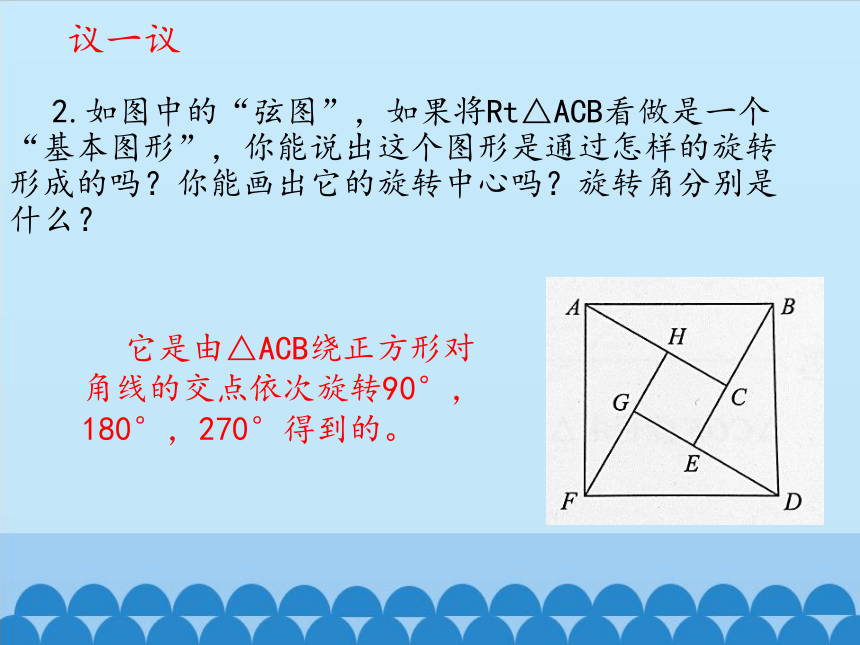
2.如图中的“弦图”,如果将Rt△ACB看做是一个“基本图形”,你能说出这个图形是通过怎样的旋转形成的吗?你能画出它的旋转中心吗?旋转角分别是什么?
它是由△ACB绕正方形对角线的交点依次旋转90°,180°,270°得到的。
议一议
例4:画一个腰长等于3的等腰直角三角形ABC,取一个锐角为45°的三角尺,把三角尺的直角顶点放在Rt△ABC的斜边BC的中点O处,并使三角尺的一条直角边经过点A,另一条直角边经过点B,如图(1)。将三角尺绕点O按顺时针方向旋转一个角度,记三角尺的两腰与Rt△ABC的两腰AB,AC的交点分别为E,F,如图(2)。在三角尺按图所示方式绕点O旋转的过程中,线段AE与CF的长度有什么关系?OE与OF的长度什么关系?证明你的结论。
解:AE=CF,OE=OF。
证明如下:
连接AO,在△AEO和△CFO中,
∵△ABC是等腰直角三角形,AO⊥BC,垂足为O,
∴∠EAO=∠C=45°,AO=OC,∠EOA=∠COF=90°-∠AOF,
∴△AEO≌△CFO(ASA),
∴AE=CF,OE=OF。
想一想
在例4中,△COF能否由△AOE旋转得到?
其旋转中心是哪个点?
旋转角度是多少度?
1.案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
答:旋转5次得到,旋转角度分别等于60°,120°,180°,240°,300°。
1.图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
2.下图可看作是一个等腰三角形通过几次旋转得到的?每次旋转多少度?
答:旋转7次得到,旋转角度分别等于45°,90°,135°,180°,225°,270°,315°。
3.如图,如果将△ABC看做“基本图形”,分析这个图案是通过怎样的旋转形成的,并画出它的旋转中心。
图案欣赏
作业:
完成课本习题4.7
谢 谢
第三课时
图形的旋转
Contents
目录
01
02
03
04
学习目标
合作探究
布置作业
05
旧知回顾
拓展练习
利用旋转的性质解决比较综合的问题。
︵
︵
F
A
B
C
D
E
O
旋转不改变图形的形状和大小。
1.旋转的定义:
在平面内,将一个图形绕一个定点沿某个方向转动一个角度,图形的这种变化称为旋转。这个定点称为旋转中心,转动的角称为旋转角。
一个图形和它经过旋转所得到的图形是全等形。
一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,任意一对对应点与旋转中心的连线所成的角都是旋转角;对应线段相等,对应角相等。
2.旋转的性质
A
O
C
D
F
E
B
1.如图,正六边形ABCDEF,它可以看作是由线段AB绕某一点按同一方向旋转5次得到的图形。
议一议
(1)你能画出旋转中心O吗?
(2)每次旋转的旋转角分别是多少度?与同伴进行交流
B
F
A
E
D
C
旋转中心为对角线AD与BE的交点。
O
每次旋转的角度分别为60°,120°,180°,240°,300°。
2.如图中的“弦图”,如果将Rt△ACB看做是一个“基本图形”,你能说出这个图形是通过怎样的旋转形成的吗?你能画出它的旋转中心吗?旋转角分别是什么?
它是由△ACB绕正方形对角线的交点依次旋转90°,180°,270°得到的。
议一议
例4:画一个腰长等于3的等腰直角三角形ABC,取一个锐角为45°的三角尺,把三角尺的直角顶点放在Rt△ABC的斜边BC的中点O处,并使三角尺的一条直角边经过点A,另一条直角边经过点B,如图(1)。将三角尺绕点O按顺时针方向旋转一个角度,记三角尺的两腰与Rt△ABC的两腰AB,AC的交点分别为E,F,如图(2)。在三角尺按图所示方式绕点O旋转的过程中,线段AE与CF的长度有什么关系?OE与OF的长度什么关系?证明你的结论。
解:AE=CF,OE=OF。
证明如下:
连接AO,在△AEO和△CFO中,
∵△ABC是等腰直角三角形,AO⊥BC,垂足为O,
∴∠EAO=∠C=45°,AO=OC,∠EOA=∠COF=90°-∠AOF,
∴△AEO≌△CFO(ASA),
∴AE=CF,OE=OF。
想一想
在例4中,△COF能否由△AOE旋转得到?
其旋转中心是哪个点?
旋转角度是多少度?
1.案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
答:旋转5次得到,旋转角度分别等于60°,120°,180°,240°,300°。
1.图案可以看作是一个菱形通过几次旋转得到的?
每次旋转了多少角度?
2.下图可看作是一个等腰三角形通过几次旋转得到的?每次旋转多少度?
答:旋转7次得到,旋转角度分别等于45°,90°,135°,180°,225°,270°,315°。
3.如图,如果将△ABC看做“基本图形”,分析这个图案是通过怎样的旋转形成的,并画出它的旋转中心。
图案欣赏
作业:
完成课本习题4.7
谢 谢
