鲁教版(五四制)数学八年级上册 1.3 公式法 第一课时 课件(共12张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 1.3 公式法 第一课时 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 108.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 00:00:00 | ||
图片预览



文档简介
(共12张PPT)
公式法
第一课时
①25x2 = (_____)2
②36a4 = (_____)2
③0.49b2 = (_____)2
④64x2y2 = (_____)2
⑤ = ( )2
回顾思考
5x
6a2
0.7b
填空:
8xy
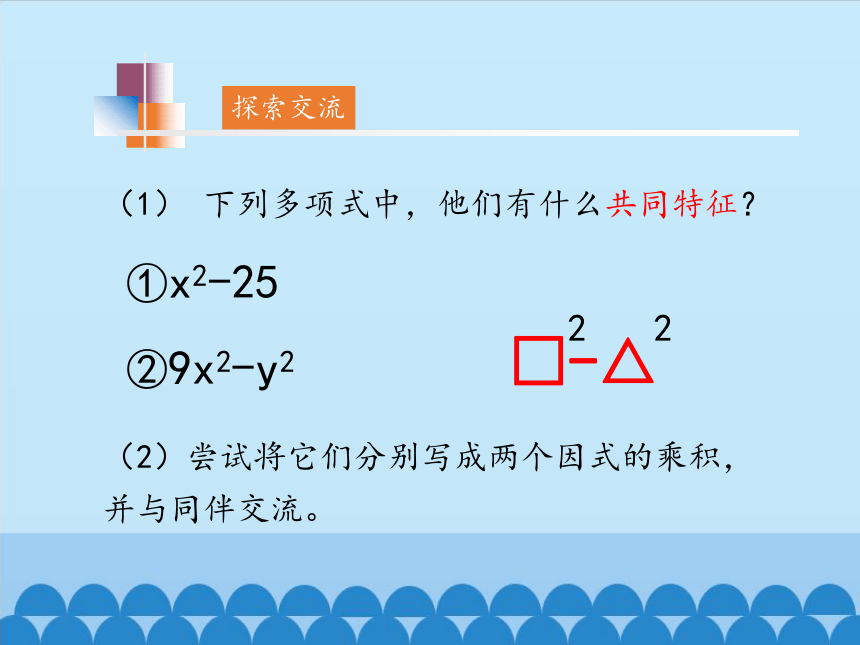
探索交流
(1) 下列多项式中,他们有什么共同特征?
(2)尝试将它们分别写成两个因式的乘积,并与同伴交流。
①x2-25
②9x2-y2
□-△
2
2
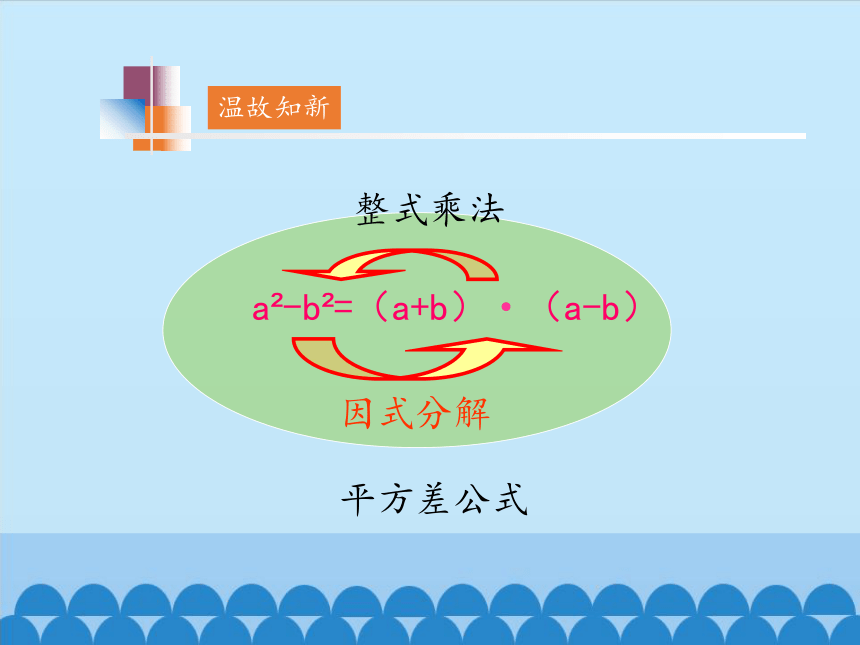
温故知新
a -b =(a+b)·(a-b)
因式分解
整式乘法
平方差公式
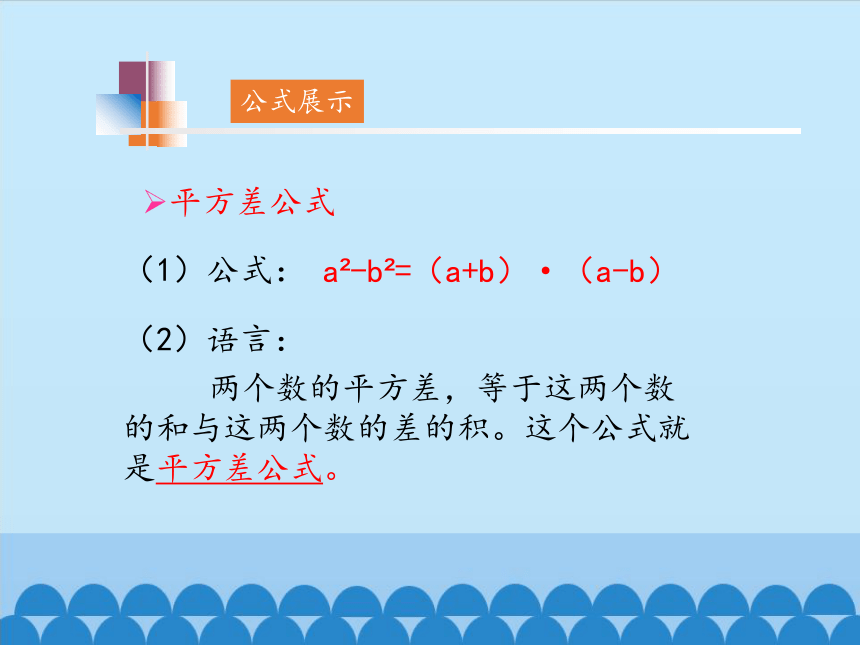
平方差公式
(1)公式:
(2)语言:
两个数的平方差,等于这两个数的和与这两个数的差的积。这个公式就是平方差公式。
a -b =(a+b)·(a-b)
公式展示
a2 b2= (a+b)(a b)
□2-△2=(□+△)(□-△)
☆2-○2=(☆+○)(☆-○)
说说平方差公式的特点:
两数的和与差的积
两个数的平方差;只有两项
形象地表示为
①左边
②右边
请在下列各式等号右边填入“+”或“-”号,使等式成立。
(1)2-a= (a-2)
(2) y-x= (x-y)
(3) b+a= (a+b)
-
(6)-m-n= (m+n)
(5)–s2+t2= (s2-t2)
(4)(b-a)2= (a-b)2
-
+
+
-
-
例题演示
例1.把下列各式分解因式:
(1)25 -16x2
解:25-16x2
=52-(4x)2
=(5+4x)(5-4x)
解:9a2- b2
=(3a)2-( b)2
=(3a+ b)(3a- b)
例题演示
例2.把下列各式分解因式:
(1)9(m+n)2-(m-n)2
(2)2x3-8x
解:原式=[3(m+n)]2-(m-n)2
=[3(m+n)+(m-n)] [3(m+n)-(m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n)
解:原式=2x(x2-4)
=2x(x2-22)
=2x(x+2)(x-2)
随堂练习
把下列各式分解因式:
(1)a2b2-m2
(2)(m-a)2-(n+b)2
(3) a2-(a+b-c)2
(4) -16x4+81y4
课堂小结
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
a2 b2=(a+b)(a b)
谢 谢
公式法
第一课时
①25x2 = (_____)2
②36a4 = (_____)2
③0.49b2 = (_____)2
④64x2y2 = (_____)2
⑤ = ( )2
回顾思考
5x
6a2
0.7b
填空:
8xy
探索交流
(1) 下列多项式中,他们有什么共同特征?
(2)尝试将它们分别写成两个因式的乘积,并与同伴交流。
①x2-25
②9x2-y2
□-△
2
2
温故知新
a -b =(a+b)·(a-b)
因式分解
整式乘法
平方差公式
平方差公式
(1)公式:
(2)语言:
两个数的平方差,等于这两个数的和与这两个数的差的积。这个公式就是平方差公式。
a -b =(a+b)·(a-b)
公式展示
a2 b2= (a+b)(a b)
□2-△2=(□+△)(□-△)
☆2-○2=(☆+○)(☆-○)
说说平方差公式的特点:
两数的和与差的积
两个数的平方差;只有两项
形象地表示为
①左边
②右边
请在下列各式等号右边填入“+”或“-”号,使等式成立。
(1)2-a= (a-2)
(2) y-x= (x-y)
(3) b+a= (a+b)
-
(6)-m-n= (m+n)
(5)–s2+t2= (s2-t2)
(4)(b-a)2= (a-b)2
-
+
+
-
-
例题演示
例1.把下列各式分解因式:
(1)25 -16x2
解:25-16x2
=52-(4x)2
=(5+4x)(5-4x)
解:9a2- b2
=(3a)2-( b)2
=(3a+ b)(3a- b)
例题演示
例2.把下列各式分解因式:
(1)9(m+n)2-(m-n)2
(2)2x3-8x
解:原式=[3(m+n)]2-(m-n)2
=[3(m+n)+(m-n)] [3(m+n)-(m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n)
解:原式=2x(x2-4)
=2x(x2-22)
=2x(x+2)(x-2)
随堂练习
把下列各式分解因式:
(1)a2b2-m2
(2)(m-a)2-(n+b)2
(3) a2-(a+b-c)2
(4) -16x4+81y4
课堂小结
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
a2 b2=(a+b)(a b)
谢 谢
