鲁教版(五四制)数学八年级上册 第四章 图形的平移与旋转 复习课件(共28张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 第四章 图形的平移与旋转 复习课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 427.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第四章 图形的平移与旋转
复习课件
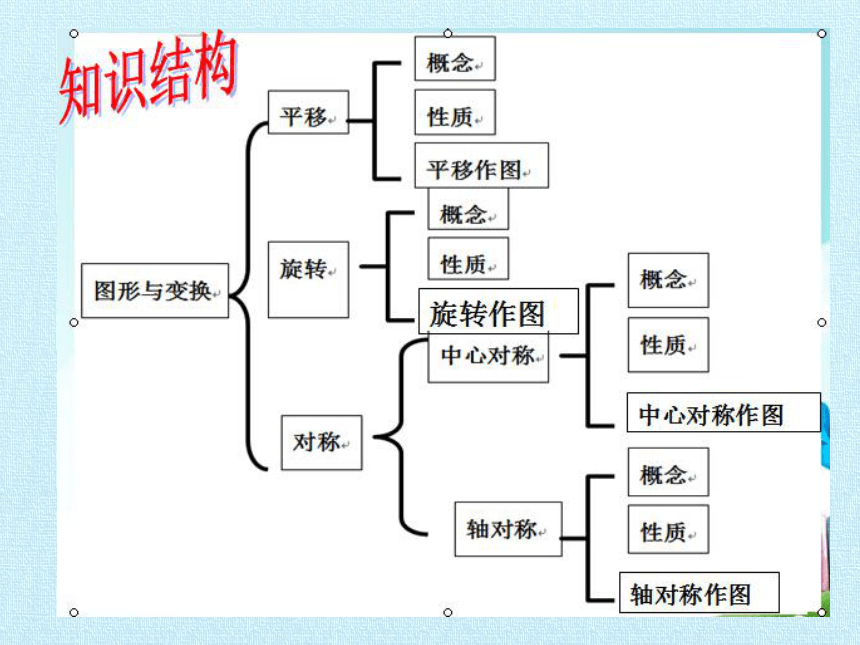
四种图形的变换方式
一、平移变换:
1.概念:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移。
2.性质:(1)平移前后图形全等;
(2)对应点连线平行或在同一直线上且相等。
3.平移的作图步骤和方法:
(1)分清题目要求,确定平移的方向和平移的距高;
(2)分析所作的图形,找出构成图形的关健点:
(3)沿一定的方向,按一定的距离平移各个关键点;
(4)连接所作的各个关键点,并标上相应的字母;
(5)写出结论。
二、旋转变换:
1.概念:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转。
说明:(1)图形的旋转是由旋转中心和旋转的角度所决定的;(2)旋转过程中旋转中心始终保持不动。(3)旋转过程中旋转的方向是相同的。(4)旋转过程静止时,图形上一个点的旋转角度是一样的,⑤旋转不改变图形的大小和形状。
2.性质:(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等。
3.旋转作图的步骤和方法:(1)确定旋转中心及旋转方向、旋转角:(2)找出图形的关键点:(3)将图形的关键点和旋转中心连接起来,然后按旋转方向分别将它们旋转一个旋转角度数,得到这些关键点的对应点;(4)按原图形顺次连接这些对应点,所得到的图形就是旋转后的图形。
说明:在旋转作图时,一对对应点与旋转中心的夹角即为旋转角。
三、中心对称
1.中心对称的有关概念:中心对称、对称中心、对称点。把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心,两个图形中的对应点叫做对称点。
2.中心对称的基本性质:
(1)成中心对称的两个图形具有图形旋转的一切性质。
(2)成中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
四、[轴对称]
有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。两个图形关于直线对称也叫做轴对称。
[图形轴对称的性质]
如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线。
旋转前后的图形完全重合
轴对称图形
中心对称图形
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
3
翻转前后的图形完全重合
两种特殊形状的图形
E
H
F
G
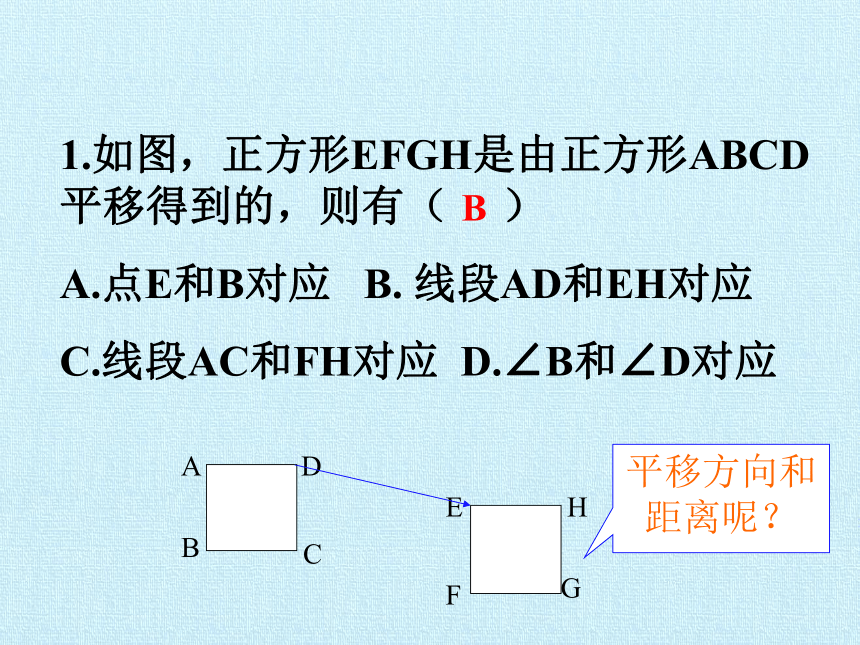
1.如图,正方形EFGH是由正方形ABCD平移得到的,则有( )
A.点E和B对应 B. 线段AD和EH对应
C.线段AC和FH对应 D.∠B和∠D对应
A
B
C
D
B
平移方向和距离呢?
2.如图△ABC是等腰直角三角形,点D是斜边BC中点,△ABD绕点A旋转到△ACE的位置,恰与△ACD组成正方形ADCE,则△ABD所经过的旋转是( )
B
C
D
E
A
A.顺时针旋转225° B.逆时针旋转45°
C.顺时针旋转315° D.逆时针旋转90°
D
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C)
(D)
D
4.经过平移,△ABC的边AB移到了EF,作出平移后的三角形。
E
F
A
B
C
5.在右图中作出“三角旗”绕O点按逆时针旋转90°后的图案。
O
6.已知四边形ABCD和点O,画四边形A'B'C'D'使它与已知四边形关于点O对称。
A
B
C
D
O
A'
B'
C'
D'
画法:
四边形A'B'C'D'就是所求的四边形。
7.下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C.图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
8.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=700,则( )
A.FG=5,∠G=700 B.EH=5,∠F=700
C.EF=5,∠F=700 D.EF=5,∠E=700
A
B
C
D
E
F
H
G
B
9.将图形 按顺时针方向旋转90度后的图形是( )
A B C D
D
10.下列图形中,不能由图形M经过一次平移或旋转得到的是( )
A
B
C
D
M
C
11.如图,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到左图,再将左图作为“基本图形”绕着A点经过逆时针连续旋转得到右图.两次旋转的角度分别为( )
A.45°,90°
B.90°,45°
C.60°,30°
D.30°,60°
A
12.如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A.ΔABC和ΔADE B.ΔABC和ΔABD
C.ΔABD和ΔACE D.ΔACE和ΔADE
B
A
C
E
D
C
13.在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A.100 B.150 C.200 D.250
B
14.如图:ΔDEF可以看作ΔABC平移得到
(1)AB∥____; ____ ∥ ____
(2)若BC=5cm, CE =3cm,则平移的
距离是____,EF= ____ cm
(3)若连结AD,与AD相等的线段是: ________
DE
AC
DF
2cm
5
BE或CF
15.如图,在ΔABC中,∠A=40o,∠C=35o,将ΔABC平移得到ΔDEF的位置,DF与BC交于点G, 你能求出∠DGB与∠E的度数吗?
16.如图:在梯形ABCD中,AD∥BC,∠B+∠C=90o,点E在AD上,先将AB向右平移,使点A与点E重合,交BC于F,再将DC向左平移,使点D与点E重合,交BC于G,请判断ΔEFG的形状
“若AD=3,FG=5,
求BC的长”
17.请说出下面乙树是怎样由甲树变换得到的?
18.如图,点E为正方形ABCD的边CD上一点,AB=5,DE=6。△DAE旋转后能与△DCF重合,(1)旋转中心是哪一点?(2)旋转了多少度?(3)如果连接EF,那么△DEF是怎样的三角形?(4)四边形DEBF的周长和面积?
19.已知正方形ABCD和正方形AEFG有一个公共点A,若将正方形AEFG绕点A按顺时针方向旋转,连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并说明理由。
1.本节课,你学到了哪些知识?
2.师友互助,给你带来了哪些帮助?
总结提升
感悟与收获:
谢 谢
第四章 图形的平移与旋转
复习课件
四种图形的变换方式
一、平移变换:
1.概念:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移。
2.性质:(1)平移前后图形全等;
(2)对应点连线平行或在同一直线上且相等。
3.平移的作图步骤和方法:
(1)分清题目要求,确定平移的方向和平移的距高;
(2)分析所作的图形,找出构成图形的关健点:
(3)沿一定的方向,按一定的距离平移各个关键点;
(4)连接所作的各个关键点,并标上相应的字母;
(5)写出结论。
二、旋转变换:
1.概念:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转。
说明:(1)图形的旋转是由旋转中心和旋转的角度所决定的;(2)旋转过程中旋转中心始终保持不动。(3)旋转过程中旋转的方向是相同的。(4)旋转过程静止时,图形上一个点的旋转角度是一样的,⑤旋转不改变图形的大小和形状。
2.性质:(1)对应点到旋转中心的距离相等;
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等。
3.旋转作图的步骤和方法:(1)确定旋转中心及旋转方向、旋转角:(2)找出图形的关键点:(3)将图形的关键点和旋转中心连接起来,然后按旋转方向分别将它们旋转一个旋转角度数,得到这些关键点的对应点;(4)按原图形顺次连接这些对应点,所得到的图形就是旋转后的图形。
说明:在旋转作图时,一对对应点与旋转中心的夹角即为旋转角。
三、中心对称
1.中心对称的有关概念:中心对称、对称中心、对称点。把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心,两个图形中的对应点叫做对称点。
2.中心对称的基本性质:
(1)成中心对称的两个图形具有图形旋转的一切性质。
(2)成中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
四、[轴对称]
有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点。两个图形关于直线对称也叫做轴对称。
[图形轴对称的性质]
如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线;轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线。
旋转前后的图形完全重合
轴对称图形
中心对称图形
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
3
翻转前后的图形完全重合
两种特殊形状的图形
E
H
F
G
1.如图,正方形EFGH是由正方形ABCD平移得到的,则有( )
A.点E和B对应 B. 线段AD和EH对应
C.线段AC和FH对应 D.∠B和∠D对应
A
B
C
D
B
平移方向和距离呢?
2.如图△ABC是等腰直角三角形,点D是斜边BC中点,△ABD绕点A旋转到△ACE的位置,恰与△ACD组成正方形ADCE,则△ABD所经过的旋转是( )
B
C
D
E
A
A.顺时针旋转225° B.逆时针旋转45°
C.顺时针旋转315° D.逆时针旋转90°
D
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C)
(D)
D
4.经过平移,△ABC的边AB移到了EF,作出平移后的三角形。
E
F
A
B
C
5.在右图中作出“三角旗”绕O点按逆时针旋转90°后的图案。
O
6.已知四边形ABCD和点O,画四边形A'B'C'D'使它与已知四边形关于点O对称。
A
B
C
D
O
A'
B'
C'
D'
画法:
四边形A'B'C'D'就是所求的四边形。
7.下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C.图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
8.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=700,则( )
A.FG=5,∠G=700 B.EH=5,∠F=700
C.EF=5,∠F=700 D.EF=5,∠E=700
A
B
C
D
E
F
H
G
B
9.将图形 按顺时针方向旋转90度后的图形是( )
A B C D
D
10.下列图形中,不能由图形M经过一次平移或旋转得到的是( )
A
B
C
D
M
C
11.如图,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到左图,再将左图作为“基本图形”绕着A点经过逆时针连续旋转得到右图.两次旋转的角度分别为( )
A.45°,90°
B.90°,45°
C.60°,30°
D.30°,60°
A
12.如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A.ΔABC和ΔADE B.ΔABC和ΔABD
C.ΔABD和ΔACE D.ΔACE和ΔADE
B
A
C
E
D
C
13.在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A.100 B.150 C.200 D.250
B
14.如图:ΔDEF可以看作ΔABC平移得到
(1)AB∥____; ____ ∥ ____
(2)若BC=5cm, CE =3cm,则平移的
距离是____,EF= ____ cm
(3)若连结AD,与AD相等的线段是: ________
DE
AC
DF
2cm
5
BE或CF
15.如图,在ΔABC中,∠A=40o,∠C=35o,将ΔABC平移得到ΔDEF的位置,DF与BC交于点G, 你能求出∠DGB与∠E的度数吗?
16.如图:在梯形ABCD中,AD∥BC,∠B+∠C=90o,点E在AD上,先将AB向右平移,使点A与点E重合,交BC于F,再将DC向左平移,使点D与点E重合,交BC于G,请判断ΔEFG的形状
“若AD=3,FG=5,
求BC的长”
17.请说出下面乙树是怎样由甲树变换得到的?
18.如图,点E为正方形ABCD的边CD上一点,AB=5,DE=6。△DAE旋转后能与△DCF重合,(1)旋转中心是哪一点?(2)旋转了多少度?(3)如果连接EF,那么△DEF是怎样的三角形?(4)四边形DEBF的周长和面积?
19.已知正方形ABCD和正方形AEFG有一个公共点A,若将正方形AEFG绕点A按顺时针方向旋转,连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并说明理由。
1.本节课,你学到了哪些知识?
2.师友互助,给你带来了哪些帮助?
总结提升
感悟与收获:
谢 谢
