鲁教版(五四制)数学八年级上册 5.1 平行四边形的性质(1)课件(共23张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 5.1 平行四边形的性质(1)课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 469.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 19:25:36 | ||
图片预览




文档简介
(共23张PPT)
第一课时
平行四边形的性质
Contents
目录
01
02
03
04
概念探索
性质探索
课堂小结
例题讲解
05
牛刀小试
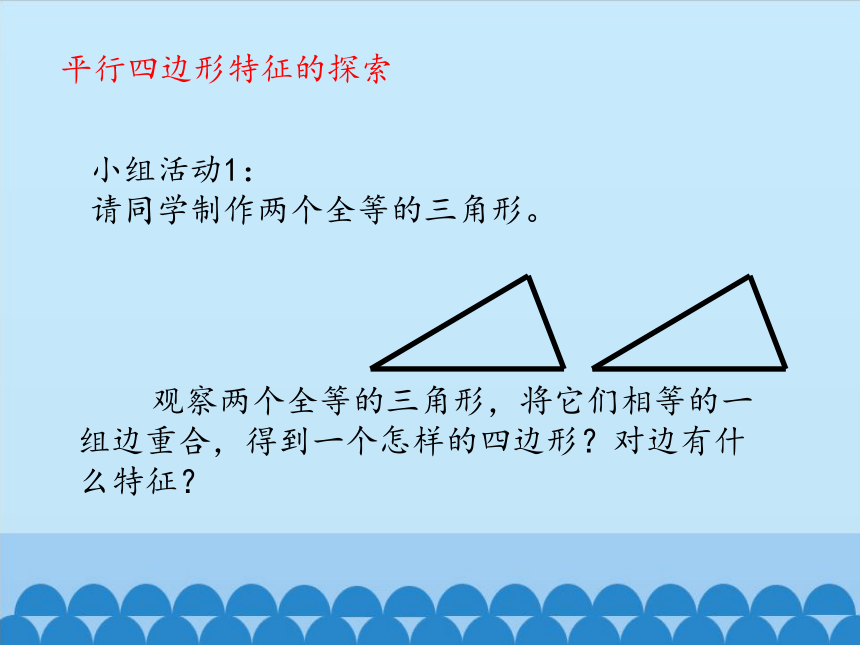
小组活动1:
请同学制作两个全等的三角形。
观察两个全等的三角形,将它们相等的一组边重合,得到一个怎样的四边形?对边有什么特征?
平行四边形特征的探索
A
B
C
D
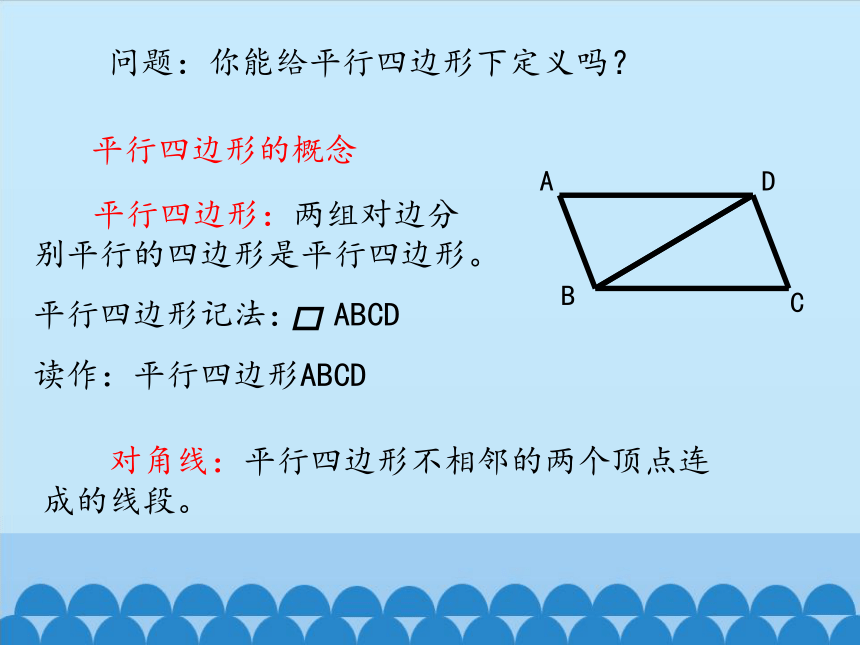
问题:你能给平行四边形下定义吗?
对角线:平行四边形不相邻的两个顶点连成的线段。
平行四边形的概念
平行四边形:两组对边分别平行的四边形是平行四边形。
平行四边形记法: ABCD
读作:平行四边形ABCD
D
C
B
A
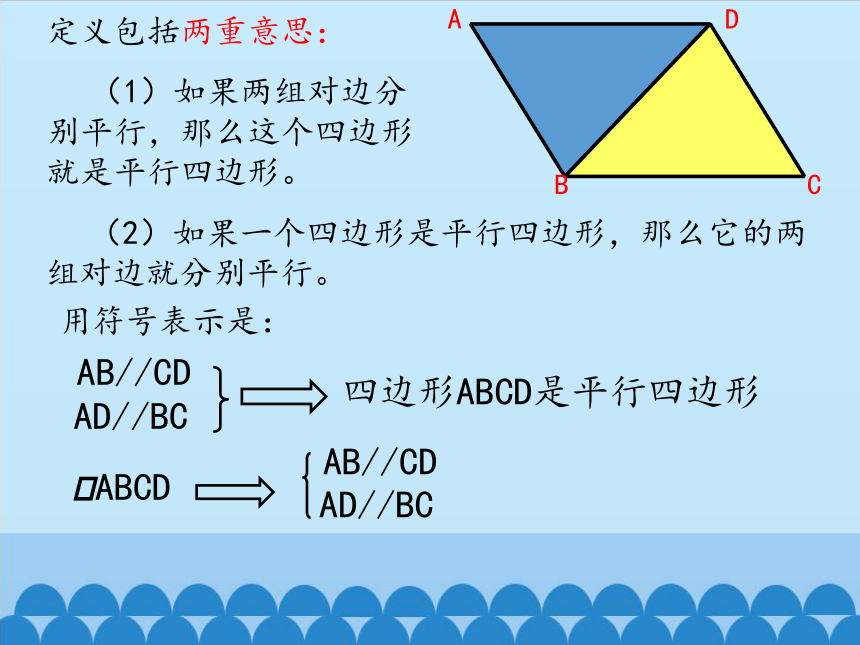
定义包括两重意思:
(1)如果两组对边分别平行,那么这个四边形就是平行四边形。
(2)如果一个四边形是平行四边形,那么它的两组对边就分别平行。
用符号表示是:
AB//CD
AD//BC
四边形ABCD是平行四边形
AB//CD
AD//BC
ABCD
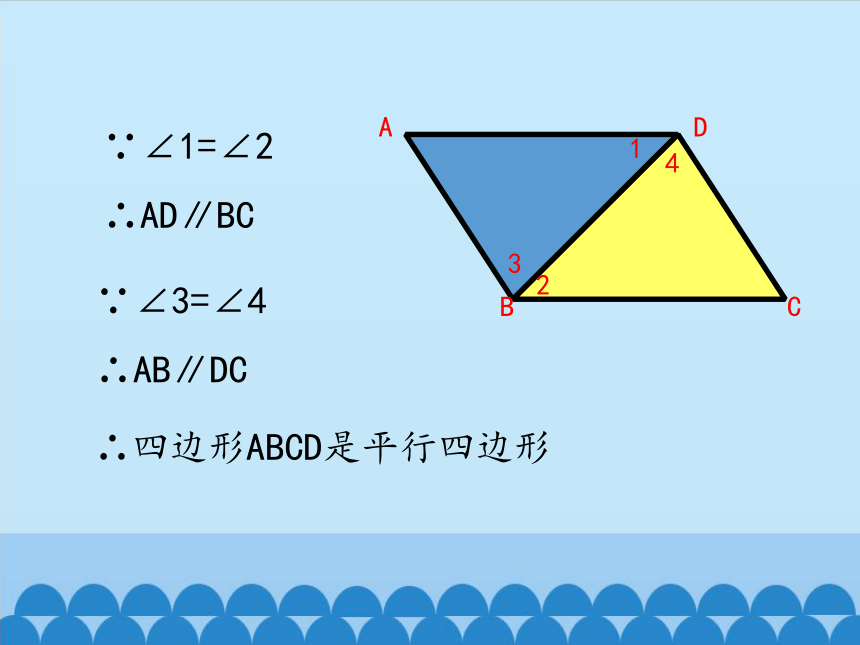
∵∠1=∠2
∴AD∥BC
D
C
B
A
1
2
3
4
∵∠3=∠4
∴AB∥DC
∴四边形ABCD是平行四边形
D
A
B
C
A
B
C
D
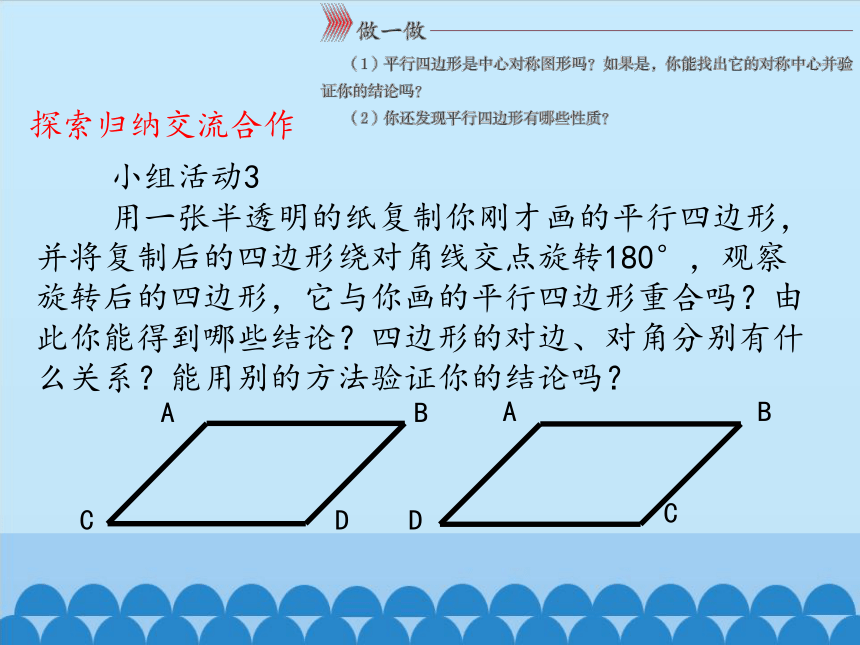
小组活动3
用一张半透明的纸复制你刚才画的平行四边形,并将复制后的四边形绕对角线交点旋转180°,观察旋转后的四边形,它与你画的平行四边形重合吗?由此你能得到哪些结论?四边形的对边、对角分别有什么关系?能用别的方法验证你的结论吗?
探索归纳交流合作
结论1:平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
结论:
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵四边形ABCD是平行四边形
∴AB=DC,AD=BC。
AB∥DC,AD∥BC。
∴∠A=∠C,∠B=∠D。
问题:
平行四边形的对边、对角分别有什么关系?
A
B
C
D
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
能用别的方法验证你的结论吗?
推理论证感悟升华
可以通过推理来证明这个结论:
例:如图,四边形ABCD是平行四边形。
求证:AB=CD,BC=AD。
证明:如图,连接AC。
∵四边形ABCD是平行四边形
∴AB//CD,BC//AD
∴∠1=∠2,∠3=∠4
∵AC=CA
∴△ABC≌△CDA(ASA)
∴AB=CD,BC=AD
4
3
1
2
你能证明平行四边形的对角相等吗?
如图,四边形ABCD是平行四边形。
求证:∠A=∠C,∠B=∠D。
证明:如图,
∵四边形ABCD是平行四边形
∴AD//BC,AB//CD
∴∠A+∠B=180°
∠A+∠D=180°
∴∠B=∠D
同理可得:∠A=∠C
例1:已知:如图,在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=CF。
求证:BE=DF。
证明:∵四边形ABCD是平行四边形
∴AB=CD
AB//CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
1. ABCD中,∠B=60°,则∠A=———,∠C=———,∠D=———。
2. ABCD中∠A比∠B大20°,则∠C=———。
3. ABCD中,AB=3cm,BC=5cm,则AD=———,CD=———。
4.如果 ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )。
A.5cm B.15cm C.6cm D.16cm
120°
120°
60°
100°
5cm
3cm
A
经历了实践与探索,你有什么感受和收获?
能给自己一个客观的评价吗?这节课你学到了什么?
2.这节课与同伴合作交流中,你向同伴学到
了什么?
3.本节课在知识和方法对你有什么启发?
作业布置
完成课本习题5.1
谢 谢
第一课时
平行四边形的性质
Contents
目录
01
02
03
04
概念探索
性质探索
课堂小结
例题讲解
05
牛刀小试
小组活动1:
请同学制作两个全等的三角形。
观察两个全等的三角形,将它们相等的一组边重合,得到一个怎样的四边形?对边有什么特征?
平行四边形特征的探索
A
B
C
D
问题:你能给平行四边形下定义吗?
对角线:平行四边形不相邻的两个顶点连成的线段。
平行四边形的概念
平行四边形:两组对边分别平行的四边形是平行四边形。
平行四边形记法: ABCD
读作:平行四边形ABCD
D
C
B
A
定义包括两重意思:
(1)如果两组对边分别平行,那么这个四边形就是平行四边形。
(2)如果一个四边形是平行四边形,那么它的两组对边就分别平行。
用符号表示是:
AB//CD
AD//BC
四边形ABCD是平行四边形
AB//CD
AD//BC
ABCD
∵∠1=∠2
∴AD∥BC
D
C
B
A
1
2
3
4
∵∠3=∠4
∴AB∥DC
∴四边形ABCD是平行四边形
D
A
B
C
A
B
C
D
小组活动3
用一张半透明的纸复制你刚才画的平行四边形,并将复制后的四边形绕对角线交点旋转180°,观察旋转后的四边形,它与你画的平行四边形重合吗?由此你能得到哪些结论?四边形的对边、对角分别有什么关系?能用别的方法验证你的结论吗?
探索归纳交流合作
结论1:平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
结论:
平行四边形的对边平行且相等。
平行四边形的对角相等。
∵四边形ABCD是平行四边形
∴AB=DC,AD=BC。
AB∥DC,AD∥BC。
∴∠A=∠C,∠B=∠D。
问题:
平行四边形的对边、对角分别有什么关系?
A
B
C
D
平行四边形的性质:
平行四边形的对边相等
平行四边形的对角相等
能用别的方法验证你的结论吗?
推理论证感悟升华
可以通过推理来证明这个结论:
例:如图,四边形ABCD是平行四边形。
求证:AB=CD,BC=AD。
证明:如图,连接AC。
∵四边形ABCD是平行四边形
∴AB//CD,BC//AD
∴∠1=∠2,∠3=∠4
∵AC=CA
∴△ABC≌△CDA(ASA)
∴AB=CD,BC=AD
4
3
1
2
你能证明平行四边形的对角相等吗?
如图,四边形ABCD是平行四边形。
求证:∠A=∠C,∠B=∠D。
证明:如图,
∵四边形ABCD是平行四边形
∴AD//BC,AB//CD
∴∠A+∠B=180°
∠A+∠D=180°
∴∠B=∠D
同理可得:∠A=∠C
例1:已知:如图,在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=CF。
求证:BE=DF。
证明:∵四边形ABCD是平行四边形
∴AB=CD
AB//CD
∴∠BAE=∠DCF
又∵AE=CF
∴△BAE≌△DCF
∴BE=DF
1. ABCD中,∠B=60°,则∠A=———,∠C=———,∠D=———。
2. ABCD中∠A比∠B大20°,则∠C=———。
3. ABCD中,AB=3cm,BC=5cm,则AD=———,CD=———。
4.如果 ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC的长是( )。
A.5cm B.15cm C.6cm D.16cm
120°
120°
60°
100°
5cm
3cm
A
经历了实践与探索,你有什么感受和收获?
能给自己一个客观的评价吗?这节课你学到了什么?
2.这节课与同伴合作交流中,你向同伴学到
了什么?
3.本节课在知识和方法对你有什么启发?
作业布置
完成课本习题5.1
谢 谢
