鲁教版(五四制)数学八年级上册 1.3 公式法(3)课件(共12张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 1.3 公式法(3)课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 19:27:07 | ||
图片预览




文档简介
(共12张PPT)
公式法
第三课时
回顾思考
目前我们所知道的因式分解的方法有几种?
2种
提公因式法
公式法
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。
通常我们把运用乘法公式进行因式分解的方法叫做公式法。
公式法
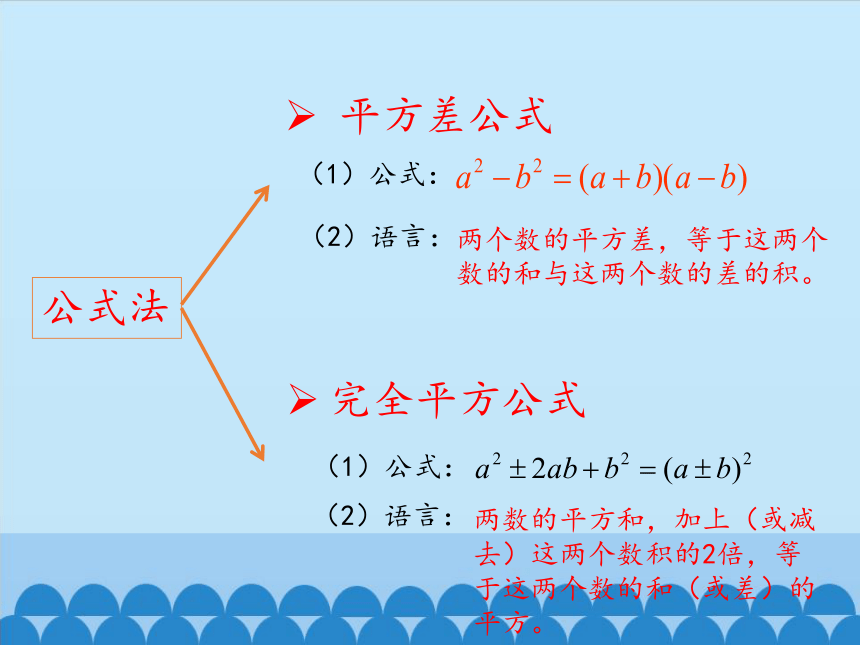
平方差公式
(1)公式:
两个数的平方差,等于这两个数的和与这两个数的差的积。
(2)语言:
完全平方公式
两数的平方和,加上(或减去)这两个数积的2倍,等于这两个数的和(或差)的平方。
(1)公式:
(2)语言:
探究
多项式x(x+6)+9能因式分解吗?与同伴进行交流
能
x(x+6)+9
=x2+6x+9
=(x+3)2
从中你学到了什么?
如果多项式不能直接分解因式,可以尝试先整理多项式,然后再分解。
例题
例5 把 因式分解
解
例6 把 因式分解
解
议一议
多项式因式分解的一般步骤是什么?与同伴进行交流
3.如果上述方法都不能分解因式,可以尝试先整理多项式,然后再分解。
1.如果多项式的各项含有公因式,那么应先提公因式。
2.如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解。
当堂练习
1.把下列各式因式分解:
(a-1)2
(m+3)(m-3)
-(x-2)2
2.把下列各式因式分解:
(x+1)2(x-1)2
(y+3)2(y-3)2
-(x+1)2(x-1)2
小结
因式分解的一般步骤
3.如果上述方法都不能分解因式,可以尝试先整理多项式,然后再分解。
1.如果多项式的各项含有公因式,那么应先提公因式。
2.如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解。
4.因式分解必须分解到每一个因式都不能再分解为止。
上述步骤可总结为:首项有“负”必先提,各项有“公”先提“公”,每项都提莫漏“1”,括号里面分到底。
作业
习题1.6
谢 谢
公式法
第三课时
回顾思考
目前我们所知道的因式分解的方法有几种?
2种
提公因式法
公式法
如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。这种分解因式的方法叫做提公因式法。
通常我们把运用乘法公式进行因式分解的方法叫做公式法。
公式法
平方差公式
(1)公式:
两个数的平方差,等于这两个数的和与这两个数的差的积。
(2)语言:
完全平方公式
两数的平方和,加上(或减去)这两个数积的2倍,等于这两个数的和(或差)的平方。
(1)公式:
(2)语言:
探究
多项式x(x+6)+9能因式分解吗?与同伴进行交流
能
x(x+6)+9
=x2+6x+9
=(x+3)2
从中你学到了什么?
如果多项式不能直接分解因式,可以尝试先整理多项式,然后再分解。
例题
例5 把 因式分解
解
例6 把 因式分解
解
议一议
多项式因式分解的一般步骤是什么?与同伴进行交流
3.如果上述方法都不能分解因式,可以尝试先整理多项式,然后再分解。
1.如果多项式的各项含有公因式,那么应先提公因式。
2.如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解。
当堂练习
1.把下列各式因式分解:
(a-1)2
(m+3)(m-3)
-(x-2)2
2.把下列各式因式分解:
(x+1)2(x-1)2
(y+3)2(y-3)2
-(x+1)2(x-1)2
小结
因式分解的一般步骤
3.如果上述方法都不能分解因式,可以尝试先整理多项式,然后再分解。
1.如果多项式的各项含有公因式,那么应先提公因式。
2.如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解。
4.因式分解必须分解到每一个因式都不能再分解为止。
上述步骤可总结为:首项有“负”必先提,各项有“公”先提“公”,每项都提莫漏“1”,括号里面分到底。
作业
习题1.6
谢 谢
