鲁教版(五四制)数学八年级上册 5.2 平行四边形的判定(3)课件(共13张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 5.2 平行四边形的判定(3)课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 317.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
第三课时
平行四边形的判定
Contents
目录
01
02
03
04
复习回顾
定理探索
课堂小结
例题演示
05
巩固练习
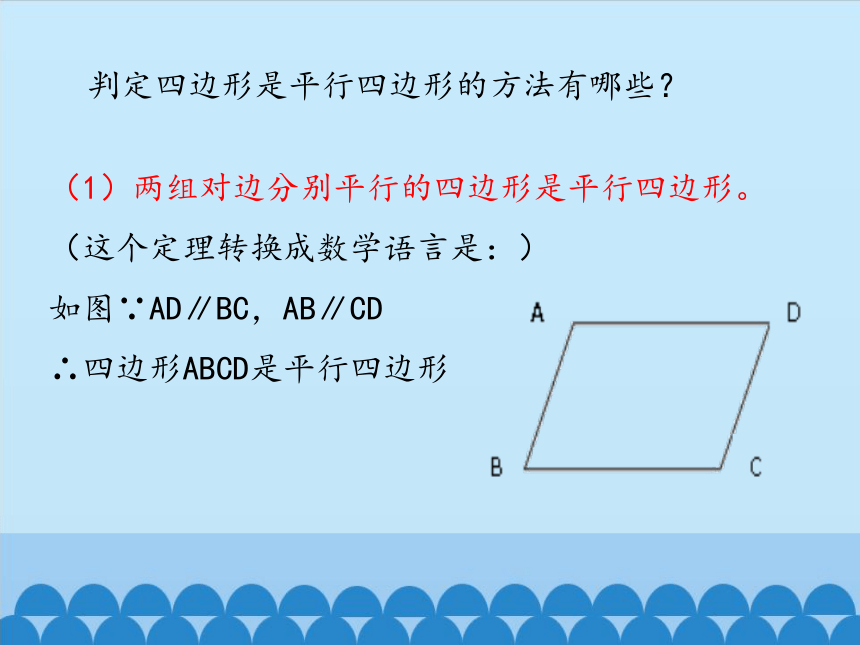
判定四边形是平行四边形的方法有哪些?
(1)两组对边分别平行的四边形是平行四边形。
(这个定理转换成数学语言是:)
如图∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
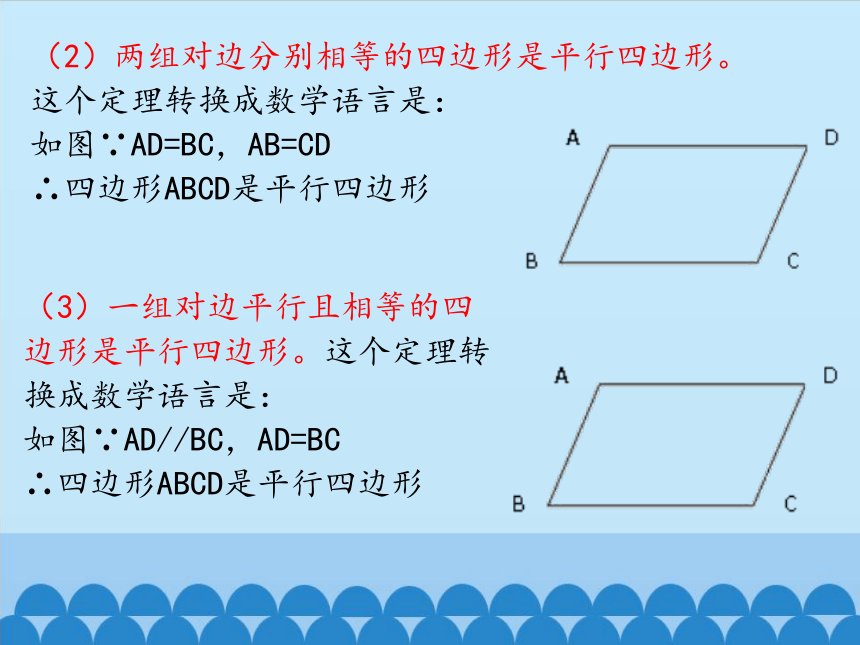
(2)两组对边分别相等的四边形是平行四边形。这个定理转换成数学语言是:
如图∵AD=BC,AB=CD
∴四边形ABCD是平行四边形
(3)一组对边平行且相等的四边形是平行四边形。这个定理转换成数学语言是:
如图∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
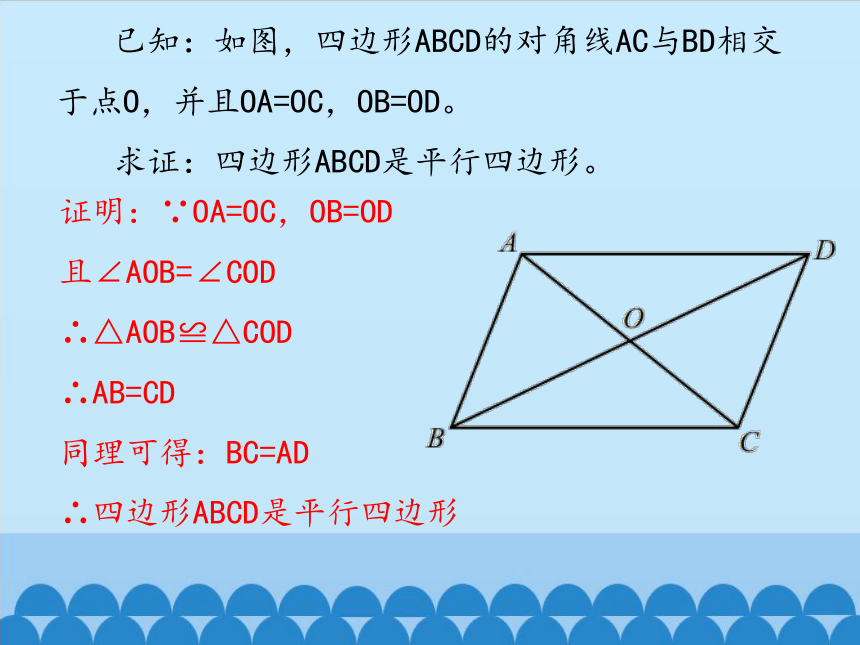
已知:如图,四边形ABCD的对角线AC与BD相交于点O,并且OA=OC,OB=OD。
求证:四边形ABCD是平行四边形。
证明:∵OA=OC,OB=OD
且∠AOB=∠COD
∴△AOB≌△COD
∴AB=CD
同理可得:BC=AD
∴四边形ABCD是平行四边形
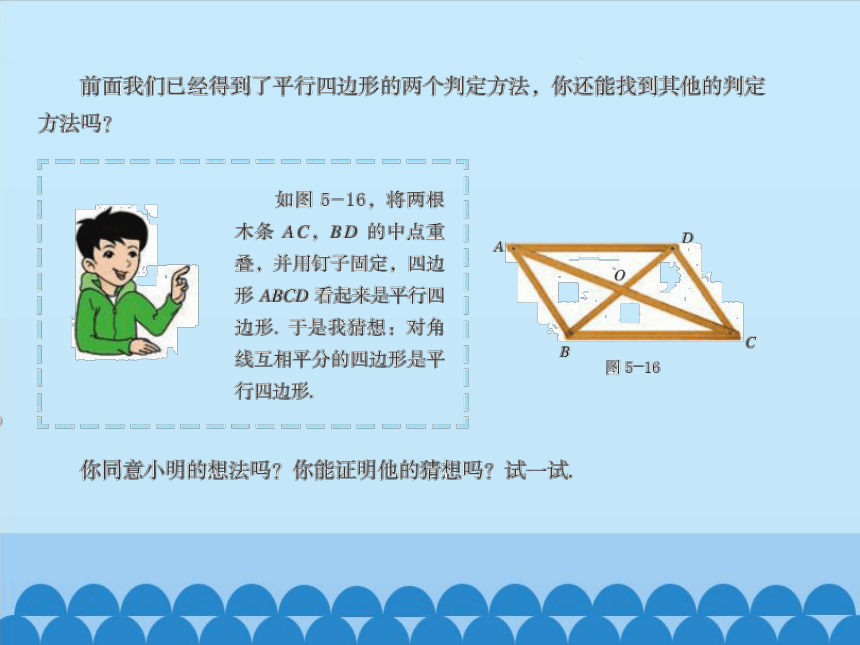
思考:
以上活动事实,能用文字语言表达吗?
平行四边形判定定理:
对角线互相平分的四边形是平行四边形
以上定理转换成数学语言是:
如图
∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
例3:已知,如图,在平行四边形ABCD中,E、F为对角线AC上两点,并且AE=CF。
求证:四边形BFDE是平行四边形吗?
证明:
如图,连接BD,交AC于点O
∵四边形ABCD是平行四边形
∴OA=OCOB=OD
又∵AE=CF
∴OA-AE=OC-CF
∴OE=OF
∴四边形BFDE是平行四边形
O
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E、F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由。
平行四边形的判定方法
2.两组对边分别相等的四边形是平行四边形
从边来判定
1.两组对边分别平行的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
作业布置
完成课本习题5.6 1、2
谢 谢
第三课时
平行四边形的判定
Contents
目录
01
02
03
04
复习回顾
定理探索
课堂小结
例题演示
05
巩固练习
判定四边形是平行四边形的方法有哪些?
(1)两组对边分别平行的四边形是平行四边形。
(这个定理转换成数学语言是:)
如图∵AD∥BC,AB∥CD
∴四边形ABCD是平行四边形
(2)两组对边分别相等的四边形是平行四边形。这个定理转换成数学语言是:
如图∵AD=BC,AB=CD
∴四边形ABCD是平行四边形
(3)一组对边平行且相等的四边形是平行四边形。这个定理转换成数学语言是:
如图∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
已知:如图,四边形ABCD的对角线AC与BD相交于点O,并且OA=OC,OB=OD。
求证:四边形ABCD是平行四边形。
证明:∵OA=OC,OB=OD
且∠AOB=∠COD
∴△AOB≌△COD
∴AB=CD
同理可得:BC=AD
∴四边形ABCD是平行四边形
思考:
以上活动事实,能用文字语言表达吗?
平行四边形判定定理:
对角线互相平分的四边形是平行四边形
以上定理转换成数学语言是:
如图
∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
例3:已知,如图,在平行四边形ABCD中,E、F为对角线AC上两点,并且AE=CF。
求证:四边形BFDE是平行四边形吗?
证明:
如图,连接BD,交AC于点O
∵四边形ABCD是平行四边形
∴OA=OCOB=OD
又∵AE=CF
∴OA-AE=OC-CF
∴OE=OF
∴四边形BFDE是平行四边形
O
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E、F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由。
平行四边形的判定方法
2.两组对边分别相等的四边形是平行四边形
从边来判定
1.两组对边分别平行的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
作业布置
完成课本习题5.6 1、2
谢 谢
