平行四边形的判定(三)[下学期]
文档属性
| 名称 | 平行四边形的判定(三)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 72.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-07 09:30:00 | ||
图片预览


文档简介
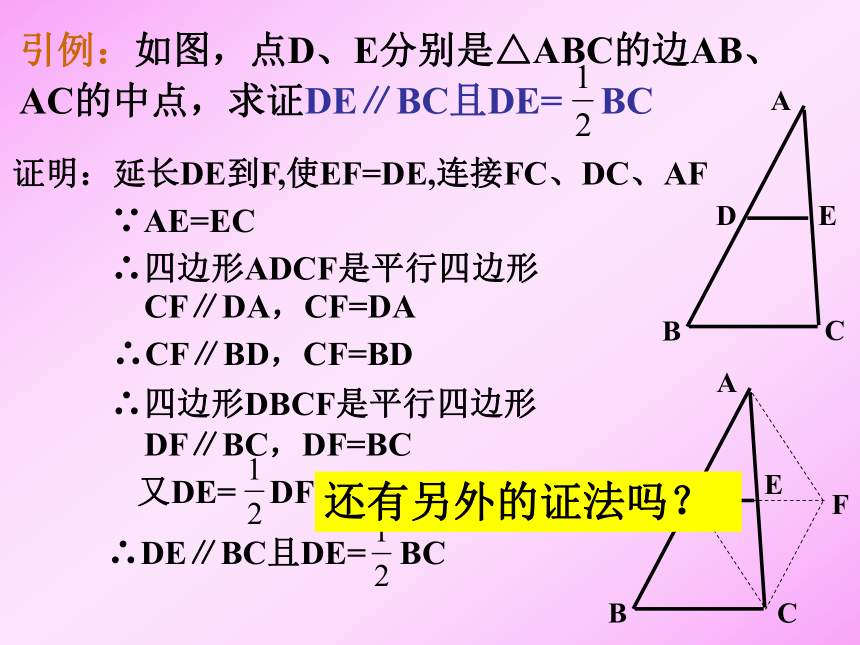
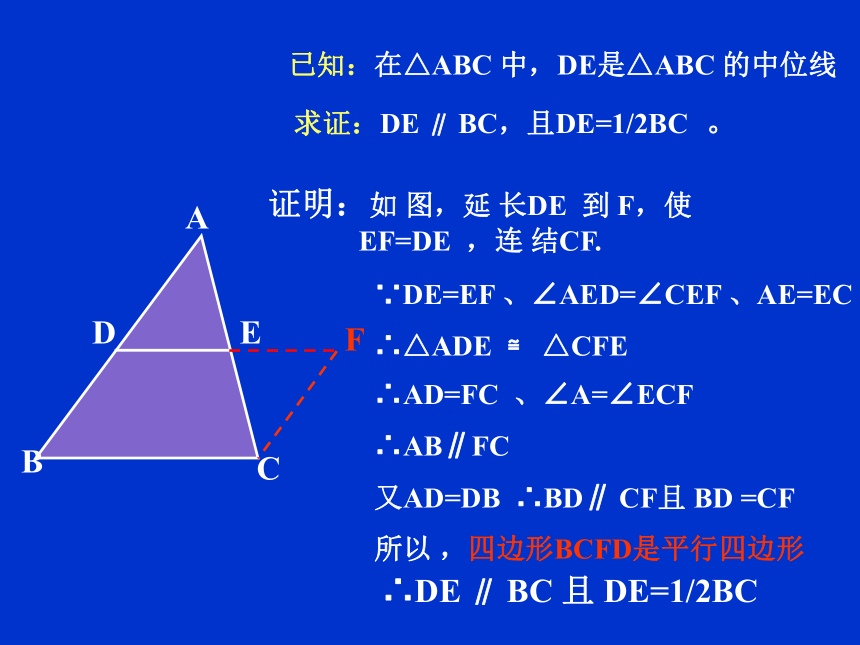
课件17张PPT。平行四边形判定(3)三角形的中位线回顾与联想:□ ABCD(1)AB∥CD, BC∥AD(2) AB=CD,BC=AD (4) ∠A= ∠C , ∠ B=∠ D(5) AO=OC, BO=OD(3) AB∥CD,AB=CDABCDO引例:如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC还有另外的证法吗?ABCDEF 已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC 。 ∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形∴DE ∥ BC 且 DE=1/2BC
定义:把连接三角形两边中点的线段叫做三角形的中位线。证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
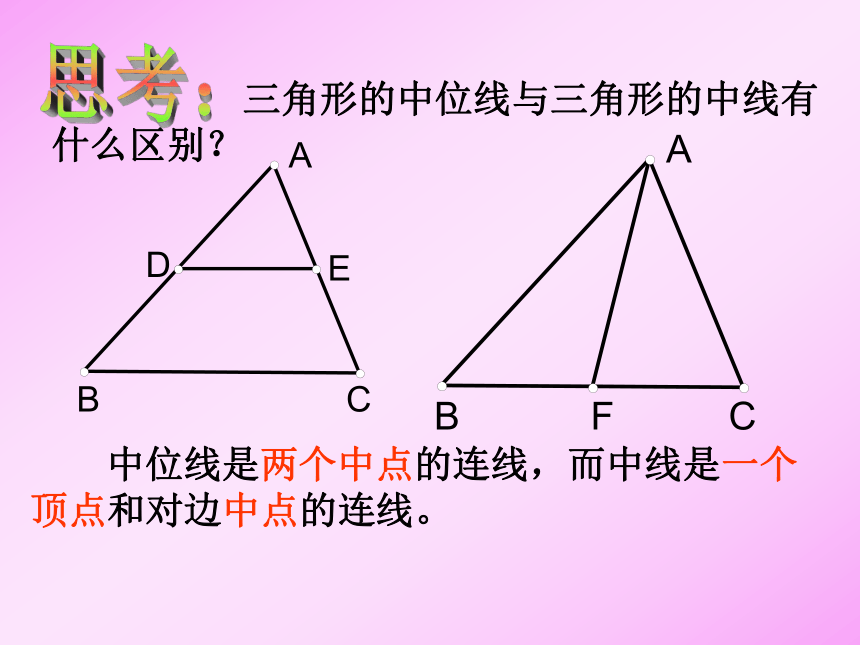
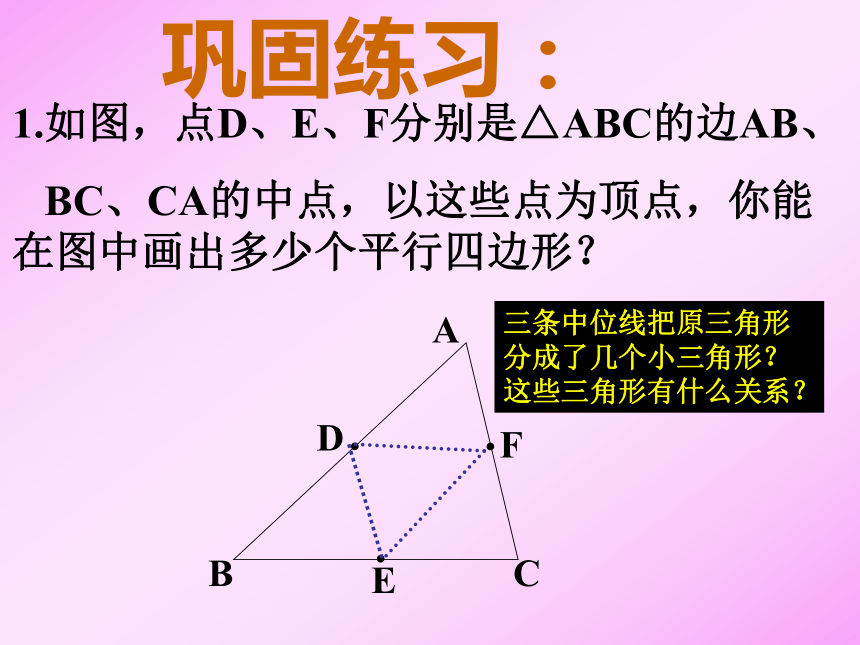
三角形的中位线与三角形的中线有什么区别?思考: 中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。巩固练习:1.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?三条中位线把原三角形分成了几个小三角形?这些三角形有什么关系?2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABCDE 例1:求证顺次连结四边形各边中点所得的四边形是平行四边形。 已知:E、F、G、H分别是四边形ABCD中AB、BC、CD、DA的中点。求证:EFGH是平行四边形。 任意四边形四边中点连线所得的四边形一定是平行四边形。例2:已知:E为平行四边形ABCD中DC边的延长
线上一点,且CE=DC,连结AE,分别交BC、BD于
点F、G,连接AC交BD于O,连结OF.
求证: AB= 2 OFADBCEGFO提示:证明△ABF≌ △ECF,
得BF=CF,再证OF是
△ABC的中位线.练一练1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
2. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.AEDCB(1)AEDBC(2) 3、△ABC中,D是AB中点,E是AC上的点,且3AE=2AC,CD、BE交于O点.
求证:OE= BE. 走进中考1.如图1,在Rt△ABC中,∠ACB=90°,点D,F分别为AC,BC的中点,CE是斜
边的中线,如果DF=3cm,
则CE=_______cm。∟ABCDEF图12.已知如图2,BD、CE分别是 △ABC的外角 平分线,过点A作AF⊥BD,AG ⊥CE,垂足分别是F、G,连结FG,延长AF、AG,与直线BC相交,求证:
FG=1/2(AB+BC+AC)ABCDEFGHHK直角三角形斜边上的中线等于斜边的一半。 思考题:已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高。求 证:∠EDG= ∠EFG。分析:EF是△ABC的中位线DG是Rt△ADC斜边上的中线∴EF=DG你还想到了什么?小 结三角形中位线定义三角形中位线定理三角形中位线定理应用注意:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线定 理 应 用:⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
求证:DE ∥ BC,且DE=1/2BC 。 ∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形∴DE ∥ BC 且 DE=1/2BC
定义:把连接三角形两边中点的线段叫做三角形的中位线。证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
三角形的中位线与三角形的中线有什么区别?思考: 中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。巩固练习:1.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?三条中位线把原三角形分成了几个小三角形?这些三角形有什么关系?2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABCDE 例1:求证顺次连结四边形各边中点所得的四边形是平行四边形。 已知:E、F、G、H分别是四边形ABCD中AB、BC、CD、DA的中点。求证:EFGH是平行四边形。 任意四边形四边中点连线所得的四边形一定是平行四边形。例2:已知:E为平行四边形ABCD中DC边的延长
线上一点,且CE=DC,连结AE,分别交BC、BD于
点F、G,连接AC交BD于O,连结OF.
求证: AB= 2 OFADBCEGFO提示:证明△ABF≌ △ECF,
得BF=CF,再证OF是
△ABC的中位线.练一练1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
2. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.AEDCB(1)AEDBC(2) 3、△ABC中,D是AB中点,E是AC上的点,且3AE=2AC,CD、BE交于O点.
求证:OE= BE. 走进中考1.如图1,在Rt△ABC中,∠ACB=90°,点D,F分别为AC,BC的中点,CE是斜
边的中线,如果DF=3cm,
则CE=_______cm。∟ABCDEF图12.已知如图2,BD、CE分别是 △ABC的外角 平分线,过点A作AF⊥BD,AG ⊥CE,垂足分别是F、G,连结FG,延长AF、AG,与直线BC相交,求证:
FG=1/2(AB+BC+AC)ABCDEFGHHK直角三角形斜边上的中线等于斜边的一半。 思考题:已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高。求 证:∠EDG= ∠EFG。分析:EF是△ABC的中位线DG是Rt△ADC斜边上的中线∴EF=DG你还想到了什么?小 结三角形中位线定义三角形中位线定理三角形中位线定理应用注意:
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线定 理 应 用:⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
