人教版 七年级上册 解一元一次方程(一) 合并同类项与移项 精品课件(共25张PPT)
文档属性
| 名称 | 人教版 七年级上册 解一元一次方程(一) 合并同类项与移项 精品课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 881.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 19:59:02 | ||
图片预览








文档简介
(共25张PPT)
11.2 解一元一次方程(一) ——合并同类项与移项
解:(1)
(2)
(3)
(4)
鸡西市第九中学“1155”尝试教学
导入新课—明确目标
1.解方程:
3x-1=20
解:方程两边同时加1,得
3x=21
方程两边同时除以3,得
x=7
1.学会用合并同类项与移项的
方法解一元一次方程;
2.培养自己的计算能力;
3.加强小组合作的意识与竞争意
识。
学习目标:
导入新课—明确目标
自学课本
1.自学内容:课本第10页
2.自学时间:2分钟
回答下列问题:
1.题中有哪几个量?
2.你能找出问题中的相等关系吗?
鸡西市第九中学“1155”尝试教学
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
设前年购买x台。可以表示出:去年购买计算机 台,今年购买计算机 台。你能找出问题中的相等关系吗?
2 x
4 x
前年购买量+去年购买量+今年购买量=140台
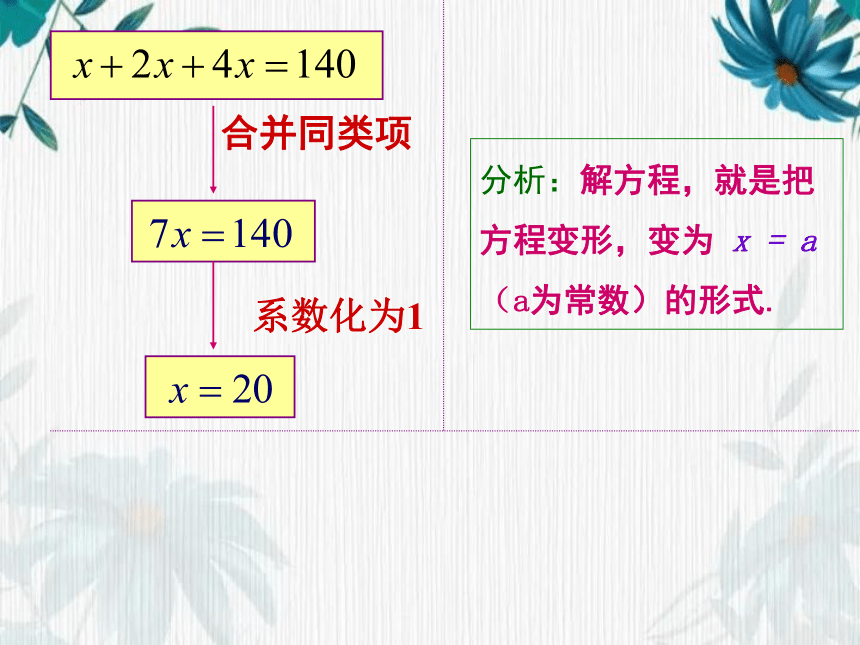
x+2x+4x=140
思考:怎样解这个方程呢?
出示问题—自主学习
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
合并同类项
系数化为1
解方程中“合并同类项”起了什么作用?
解方程中的“合并”是利用分配律将含有未知数的项和常数项分别合并为一项。它使方程变得简单,更接近x = a的形式
想一想:
例1:解方程
解:
尝试练习—互动探究
练习1:解下列方程
你一定会!
解:(1)合并同类项,得
系数化为1,得
(2)合并同类项,得
系数化为1,得
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出 本,加上剩余
的20本,这批书共 本.
每人分4本,需要 本,减去缺少
的25本,这批书共 本.
设这个班有x名学生.
这批书的总数有几种表示法?它们之间有什么关系?
问题2:
提问1:怎样解这个方程?它与原来遇到的方程有何不同?
3x+20 = 4x-25
方程的两边都有含x的项(3x与4x)和不含字母的常数项(20与-25).
3x+20=4x-25
3x+20-4x=4x-25-4x
3x+20-4x= -25
3x+20-4x-20=-25-20
3x-4x=-25-20
(合并同类项)
(利用等式性质1)
(利用等式性质1)
(合并同类项)
提问2:如何才能使这个方程向x=a的形式转化?
3x +20 = 4x -25
3x-4x=-25 -20
把等式一边的某项变号后移到另一边,叫做移项.(教材P12)
注:移项要变号
移 项
合并同类项
系数化为1
像这样,把等式一边的某项变号后移到另一边,叫做移项.
移项变号
下面的框图表示了解这个方程的具体过程:
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式.
提问4: “移项”起了什么作用?
提问3:以上解方程“移项”的依据是什么?
移项的依据是等式的性质1
阿尔-花拉子米(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。
《对消与还原》
现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?
“对消”与“还原”就是“合并”与“移项”
练习1:把下列方程进行移项变换
5
x
x
(-3x)
5
9x
(-3)
解方程
解:移项,得
合并同类项,得
系数化为1,得
交流展示—精讲点拨
练习2:解下列方程
(1)
解:移项,得 -x-3x=2-8
系数化为1,得
合并同类项,得 -4x=-6
b=-6
1、今天你又学会了解方程的哪些方法?有哪些步聚?
每一步的依据是什么?
移项(等式的性质1)
合并同类项(分配律)
系数化为1(等式的性质2)
注意变号哦!
这节课我们学习了什么?
解下列一元一次方程
再次尝试—当堂检测
解下列一元一次方程:
再次尝试—当堂检测
课后作业: 1.习题11.2 1、3;
2.资源评价:10、11页
11.2 解一元一次方程(一) ——合并同类项与移项
解:(1)
(2)
(3)
(4)
鸡西市第九中学“1155”尝试教学
导入新课—明确目标
1.解方程:
3x-1=20
解:方程两边同时加1,得
3x=21
方程两边同时除以3,得
x=7
1.学会用合并同类项与移项的
方法解一元一次方程;
2.培养自己的计算能力;
3.加强小组合作的意识与竞争意
识。
学习目标:
导入新课—明确目标
自学课本
1.自学内容:课本第10页
2.自学时间:2分钟
回答下列问题:
1.题中有哪几个量?
2.你能找出问题中的相等关系吗?
鸡西市第九中学“1155”尝试教学
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
设前年购买x台。可以表示出:去年购买计算机 台,今年购买计算机 台。你能找出问题中的相等关系吗?
2 x
4 x
前年购买量+去年购买量+今年购买量=140台
x+2x+4x=140
思考:怎样解这个方程呢?
出示问题—自主学习
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
合并同类项
系数化为1
解方程中“合并同类项”起了什么作用?
解方程中的“合并”是利用分配律将含有未知数的项和常数项分别合并为一项。它使方程变得简单,更接近x = a的形式
想一想:
例1:解方程
解:
尝试练习—互动探究
练习1:解下列方程
你一定会!
解:(1)合并同类项,得
系数化为1,得
(2)合并同类项,得
系数化为1,得
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出 本,加上剩余
的20本,这批书共 本.
每人分4本,需要 本,减去缺少
的25本,这批书共 本.
设这个班有x名学生.
这批书的总数有几种表示法?它们之间有什么关系?
问题2:
提问1:怎样解这个方程?它与原来遇到的方程有何不同?
3x+20 = 4x-25
方程的两边都有含x的项(3x与4x)和不含字母的常数项(20与-25).
3x+20=4x-25
3x+20-4x=4x-25-4x
3x+20-4x= -25
3x+20-4x-20=-25-20
3x-4x=-25-20
(合并同类项)
(利用等式性质1)
(利用等式性质1)
(合并同类项)
提问2:如何才能使这个方程向x=a的形式转化?
3x +20 = 4x -25
3x-4x=-25 -20
把等式一边的某项变号后移到另一边,叫做移项.(教材P12)
注:移项要变号
移 项
合并同类项
系数化为1
像这样,把等式一边的某项变号后移到另一边,叫做移项.
移项变号
下面的框图表示了解这个方程的具体过程:
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式.
提问4: “移项”起了什么作用?
提问3:以上解方程“移项”的依据是什么?
移项的依据是等式的性质1
阿尔-花拉子米(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。
《对消与还原》
现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?
“对消”与“还原”就是“合并”与“移项”
练习1:把下列方程进行移项变换
5
x
x
(-3x)
5
9x
(-3)
解方程
解:移项,得
合并同类项,得
系数化为1,得
交流展示—精讲点拨
练习2:解下列方程
(1)
解:移项,得 -x-3x=2-8
系数化为1,得
合并同类项,得 -4x=-6
b=-6
1、今天你又学会了解方程的哪些方法?有哪些步聚?
每一步的依据是什么?
移项(等式的性质1)
合并同类项(分配律)
系数化为1(等式的性质2)
注意变号哦!
这节课我们学习了什么?
解下列一元一次方程
再次尝试—当堂检测
解下列一元一次方程:
再次尝试—当堂检测
课后作业: 1.习题11.2 1、3;
2.资源评价:10、11页
