平行四边形的判定[下学期]
文档属性
| 名称 | 平行四边形的判定[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 592.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-10 00:00:00 | ||
图片预览





文档简介
课件20张PPT。平行四边形的判别 1平行四边形的性质:边平行四边形的对边平行平行四边形的对边相等角平行四边形的对角相等平行四边形的邻角互补对角线 平行四边形的对角线
互相平分 温故知新 请根据平行四边形的性质进行大胆猜想平行四边形的其它的判定方法!
两组对边分别平行的四边形是平行四边形!我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
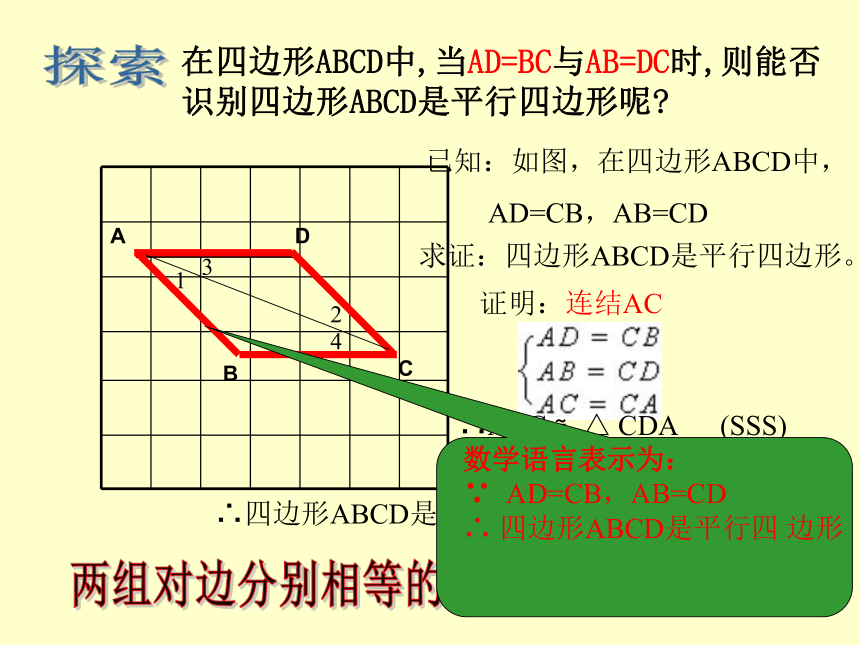
(1)根据定义:ADCB探索两组对边分别相等的四边形是平行四边形.在四边形ABCD中,当AD=BC与AB=DC时,则能否识别四边形ABCD是平行四边形呢?1423已知:如图,在四边形ABCD中,
AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS)∴∠1=∠2,∠3=∠4∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义) 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
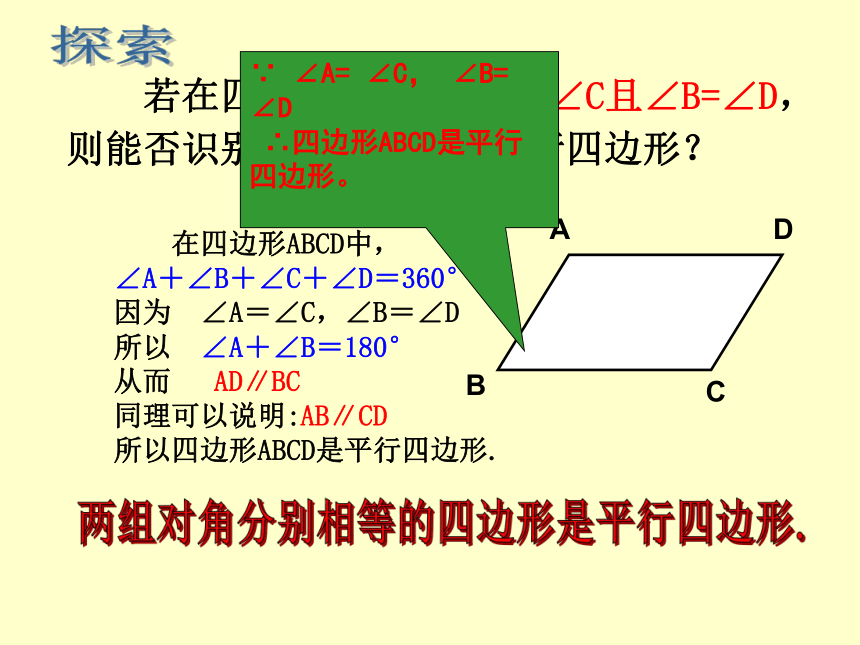
大家都困惑了……请你帮忙 若在四边形ABCD中,∠A=∠C且∠B=∠D,
则能否识别四边形ABCD为平行四边形?探索 在四边形ABCD中,
∠A+∠B+∠C+∠D=360°
因为 ∠A=∠C,∠B=∠D
所以 ∠A+∠B=180°
从而 AD∥BC
同理可以说明:AB∥CD
所以四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
∵ ∠A= ∠C, ∠B= ∠D
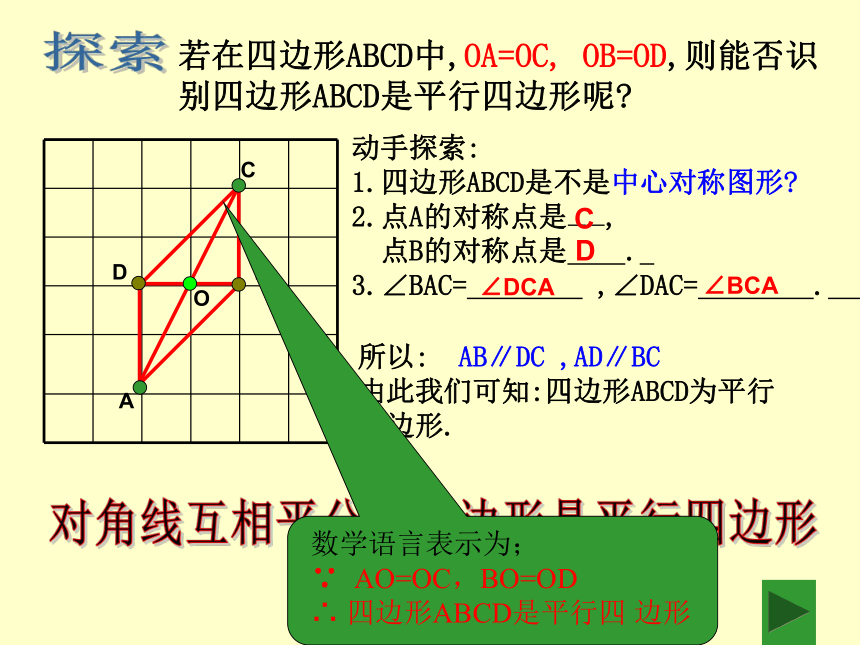
∴四边形ABCD是平行四边形。对角线互相平分的四边形是平行四边形若在四边形ABCD中,OA=OC, OB=OD,则能否识别四边形ABCD是平行四边形呢?ACBOD探索所以: AB∥DC ,AD∥BC
由此我们可知:四边形ABCD为平行
四边形.
动手探索:
1.四边形ABCD是不是中心对称图形?
2.点A的对称点是——,
点B的对称点是 .
3.∠BAC= ,∠DAC= .
CD∠DCA∠BCA 小丽说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”
你知道是为什么吗?O感悟2.从角与角的关系: 3.从对角线的相互关系: 1.从边与边的关系:平行四边形的判定方法请你识别下列四边形哪些是平行四边形?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.小试牛刀 如图, AB=CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗?你有几种判别方法?创新训练已知:如图,在平行四边形ABCD中,AE、CF分别是∠DAB、 ∠BCD的平分线。
求证:四边形AFCE是平行四边形c123证明:∵ABCD是平行四边形∴∠DAB = ∠BCD又∵AE、CF分别是∠DAB 、 ∠BCD的平分线∴ ∠1 = ∠3∵DC∥AB∴∠1 = ∠2∴∠2 =∠ 3∴AE//FC∴四边形AFCE是平行四边形由DC∥AB、AE//FC
如图在 ABCD中,E、F、G、H 分别是各边上的点,且AE=CF,BG=DH ,求证:EF与GH互相平分。探索交流做一做 如图所示,在 ABCD中,E、F分别是AB 、 CD的中点.下图中有几个平行四边形? 请说明理由.
如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO 在四边形ABCD中,若分别给出四个条件:
⑴AB∥CD ⑵AD=BC ⑶∠A=∠C ⑷AD∥ BC
现在,以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号)挑战自我平行四边形的主要性质:平行四边形两组对边分别平行两组对边分别相等两组对角分别相等对角线互相平分平行四边形的判定2.从角与角的关系: 3.从对角线的相互关系: 1.从边与边的关系:
互相平分 温故知新 请根据平行四边形的性质进行大胆猜想平行四边形的其它的判定方法!
两组对边分别平行的四边形是平行四边形!我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:ADCB探索两组对边分别相等的四边形是平行四边形.在四边形ABCD中,当AD=BC与AB=DC时,则能否识别四边形ABCD是平行四边形呢?1423已知:如图,在四边形ABCD中,
AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS)∴∠1=∠2,∠3=∠4∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义) 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙 若在四边形ABCD中,∠A=∠C且∠B=∠D,
则能否识别四边形ABCD为平行四边形?探索 在四边形ABCD中,
∠A+∠B+∠C+∠D=360°
因为 ∠A=∠C,∠B=∠D
所以 ∠A+∠B=180°
从而 AD∥BC
同理可以说明:AB∥CD
所以四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形。对角线互相平分的四边形是平行四边形若在四边形ABCD中,OA=OC, OB=OD,则能否识别四边形ABCD是平行四边形呢?ACBOD探索所以: AB∥DC ,AD∥BC
由此我们可知:四边形ABCD为平行
四边形.
动手探索:
1.四边形ABCD是不是中心对称图形?
2.点A的对称点是——,
点B的对称点是 .
3.∠BAC= ,∠DAC= .
CD∠DCA∠BCA 小丽说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”
你知道是为什么吗?O感悟2.从角与角的关系: 3.从对角线的相互关系: 1.从边与边的关系:平行四边形的判定方法请你识别下列四边形哪些是平行四边形?说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.小试牛刀 如图, AB=CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗?你有几种判别方法?创新训练已知:如图,在平行四边形ABCD中,AE、CF分别是∠DAB、 ∠BCD的平分线。
求证:四边形AFCE是平行四边形c123证明:∵ABCD是平行四边形∴∠DAB = ∠BCD又∵AE、CF分别是∠DAB 、 ∠BCD的平分线∴ ∠1 = ∠3∵DC∥AB∴∠1 = ∠2∴∠2 =∠ 3∴AE//FC∴四边形AFCE是平行四边形由DC∥AB、AE//FC
如图在 ABCD中,E、F、G、H 分别是各边上的点,且AE=CF,BG=DH ,求证:EF与GH互相平分。探索交流做一做 如图所示,在 ABCD中,E、F分别是AB 、 CD的中点.下图中有几个平行四边形? 请说明理由.
如图,在 ?ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO 在四边形ABCD中,若分别给出四个条件:
⑴AB∥CD ⑵AD=BC ⑶∠A=∠C ⑷AD∥ BC
现在,以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号)挑战自我平行四边形的主要性质:平行四边形两组对边分别平行两组对边分别相等两组对角分别相等对角线互相平分平行四边形的判定2.从角与角的关系: 3.从对角线的相互关系: 1.从边与边的关系:
