三角形的内角和(课件)-四年级下册数学冀教版(共26张PPT)
文档属性
| 名称 | 三角形的内角和(课件)-四年级下册数学冀教版(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 626.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 00:00:00 | ||
图片预览

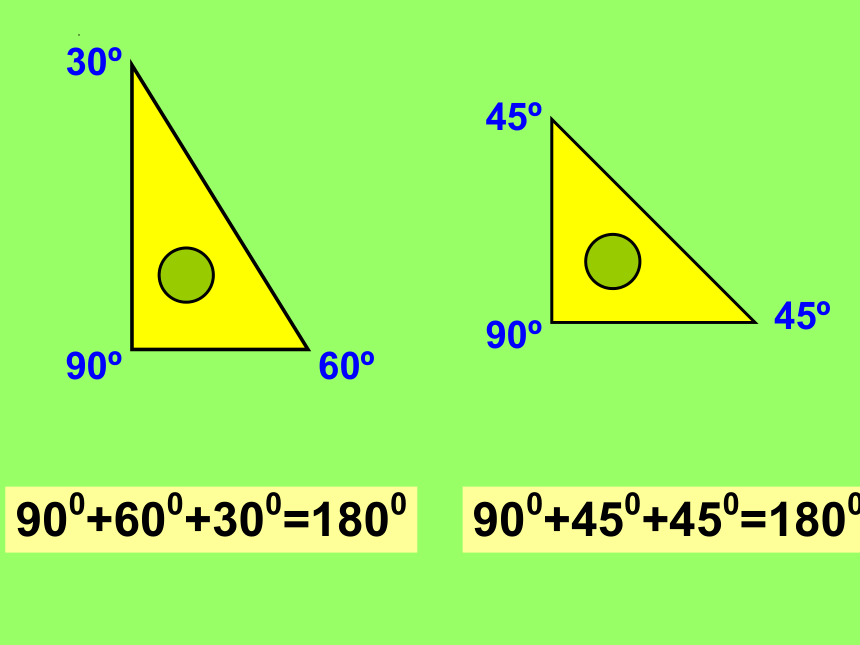

文档简介
(共26张PPT)
三角形的内角和
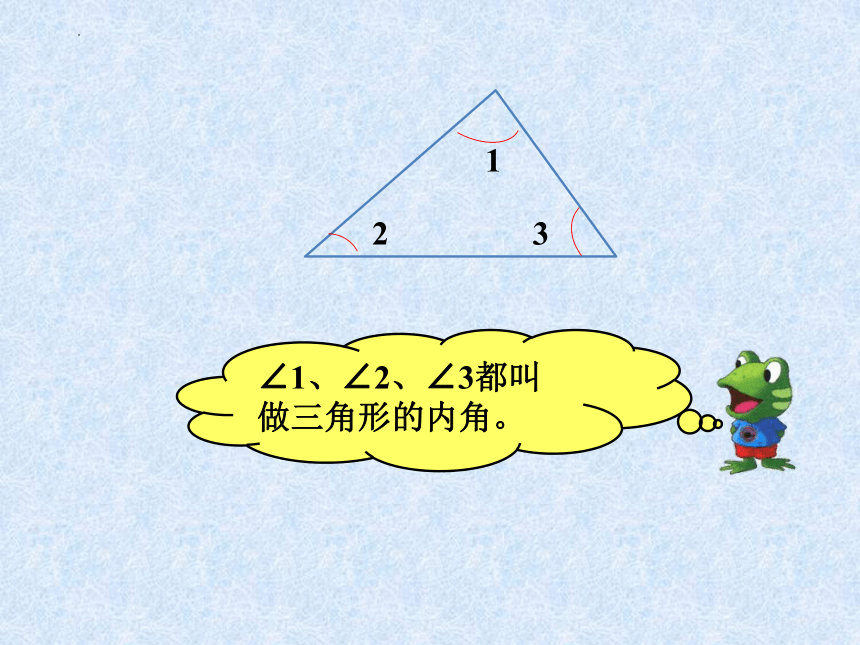
1
2
3
∠1、∠2、∠3都叫做三角形的内角。
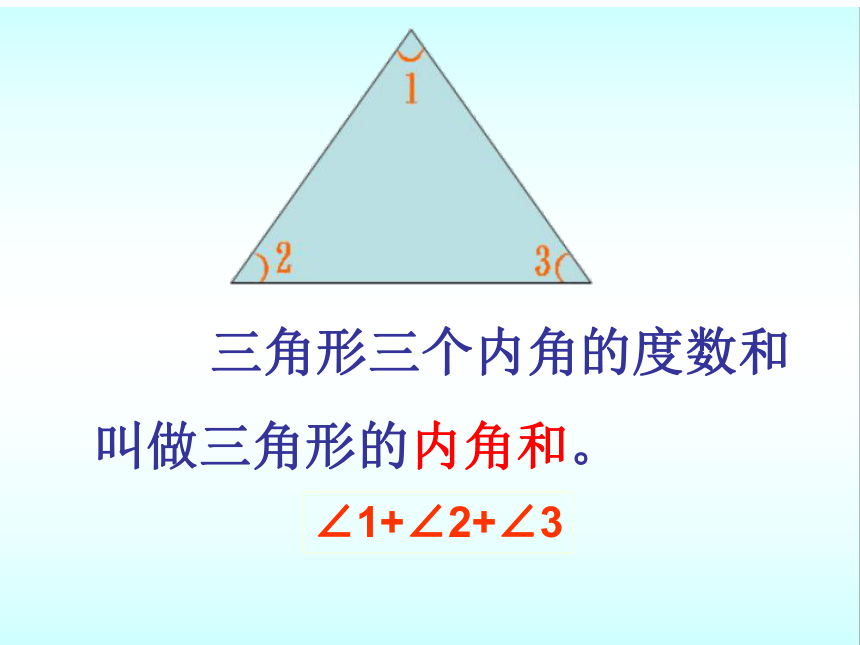
三角形三个内角的度数和
叫做三角形的内角和。
∠1+∠2+∠3
900+600+300=1800
900+450+450=1800
90
45
45
30
60
90
任意画一个三角形,
测量三个内角的度数并求和。
量一量,算一算
1
1
2
2
3
3
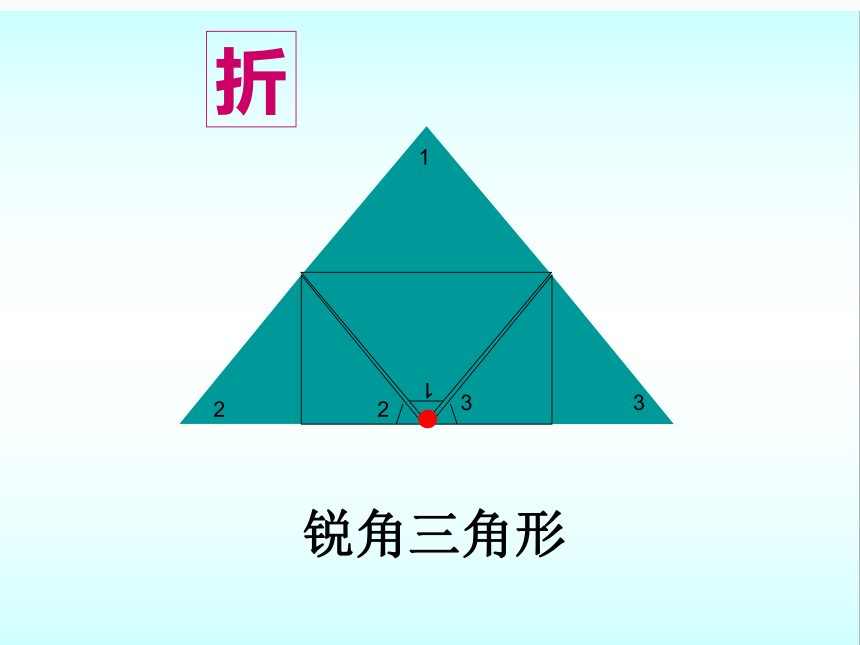
折
锐角三角形
·
折
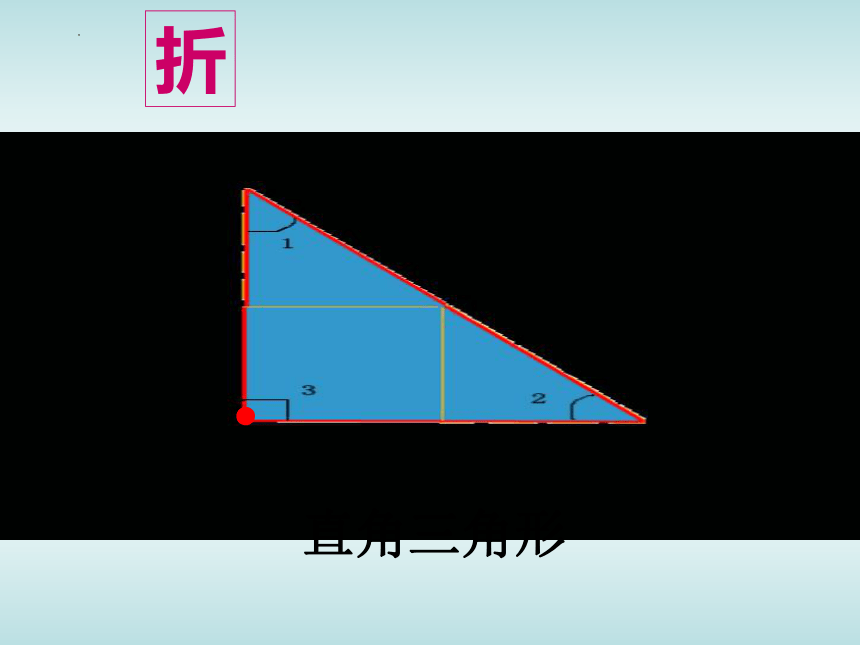
直角三角形
·
1
1
2
2
3
3
折
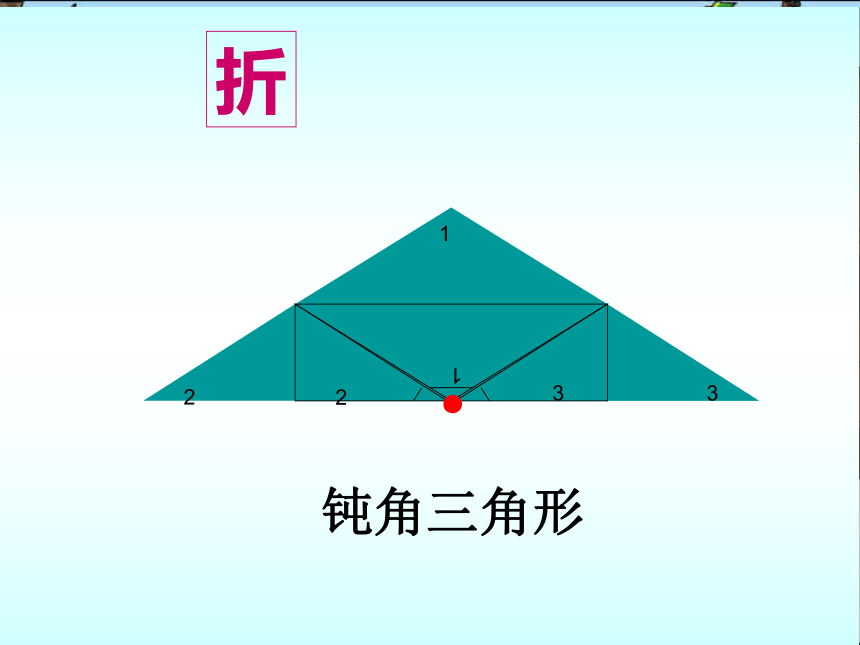
钝角三角形
·
3
2
3
1
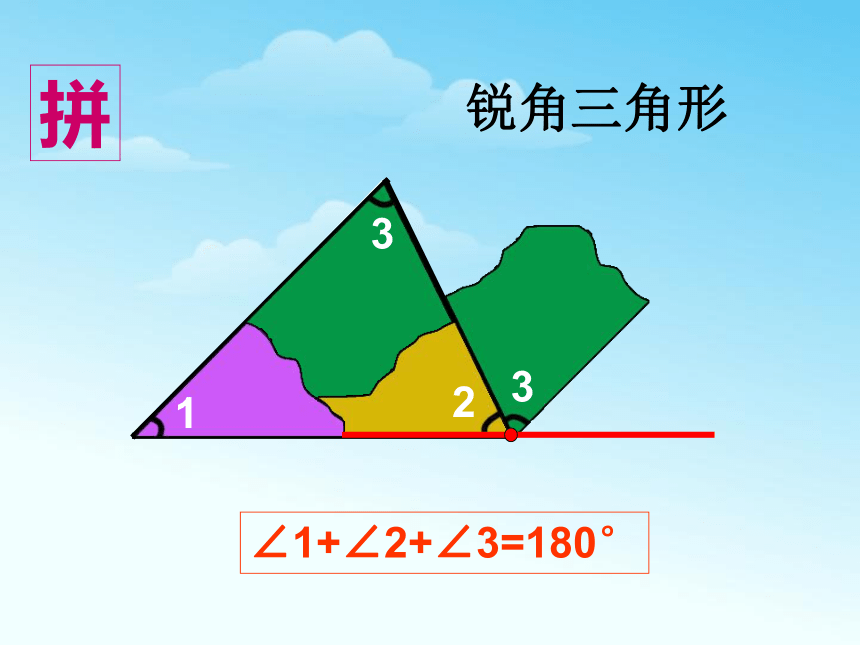
拼
∠1+∠2+∠3=180°
锐角三角形
∠1+∠2+∠3=180°
拼
2
1
3
3
直角三角形
拼
3
2
1
3
∠1+∠2+∠3=180°
钝角三角形
任意三角形的内角和都是180°
结论:
A、90°
B、比90°大
C、可能等于90°,大于90°或小于90°
D、还是180°
1、把一个三角形从一个顶点用一条
直线分成两个三角形,其中一个三角形
的内角和( )
D
1
2
3
4
5
6
2、一块三角尺的内角和是180度,用两块完全
一样的三角尺拼成一个三角形,这个三角形
的内角和是360度?
一块三角尺的内角和是180度,用两块完全
一样的三角尺拼成一个三角形,这个三角形
的内角和( )。
180°
2
1
3
3、三角形中,∠1=750,∠2=390,
求∠3的度数
180 —75 —39
=105 —39
=660
180 —(75 +39 )
=180 —114
=660
答:∠3是660
1800—750—390
=1050—390
=660
1800—(750+390)
=1800—1140
=660
4、想一想:在一个直角三角形中,
已知一个锐角是52度,能求出
另一个锐角是多少度吗?
1800—900—520
=900—520
=380
1800—(900+520)
=1800—1420
=380
52°
90°
答:另一个锐角是
52°
5、(1)∠1=30° ∠2=50° ∠3= ( )
这是( )三角形
(2)∠1=50° ∠3=40° ∠2= ( )
这是( )三角形
(3)∠2=70° ∠3=30° ∠1= ( )
这是( )三角形
填一填
100°
90°
80°
钝角
直角
锐角
等腰三角形的两个底角相等。
等边三角形的三个角相等,每个角都是60°。
6、如图,在等腰三角形中,其中底角∠1=65 ,则顶角
∠2=( ).
50°
180 - 65 ×2
=180 -130
=50
2
3
1
65
65
已知底角
7、三角形中,∠1=300,∠2=∠3,求∠3
1
2
3
(1800—300 )÷2
= 1500÷2
= 750
答:∠3是750
30
已知顶角
8、一个等腰三角形,它的一个角的度数是800,求另外两个角的度数。
当80 是顶角时,
(1800—800 )÷2
= 1000÷2
= 500
答:另外两个角是500和500或者800 和200
80
80
80
当80 是底角时,
1800—800—800
= 1000—800
= 200
9、一个等腰三角形,它的一个角的度数是1000,求另外两个角的度数。
100 是顶角
(1800—1000 )÷2
= 800÷2
= 400
答:另外两个角都是400
100
100
100
10、如图,在直角三角形中∠1=35 ,
求∠2=( ),∠3=( ).
1
2
3
55°
125°
∠2 =180 - 90 - ∠1
∠3=180 - ∠2
提示:
帕斯卡(BlaisePascal,1623~1662) ,法国数学家、物理学家、近代概率论的奠基者。早在300多年前这位法国著名的科学家就已经发现了任何三角形的内角和是180°,而他当时才12岁。
三角形的内角和
三角形的内角和
1
2
3
∠1、∠2、∠3都叫做三角形的内角。
三角形三个内角的度数和
叫做三角形的内角和。
∠1+∠2+∠3
900+600+300=1800
900+450+450=1800
90
45
45
30
60
90
任意画一个三角形,
测量三个内角的度数并求和。
量一量,算一算
1
1
2
2
3
3
折
锐角三角形
·
折
直角三角形
·
1
1
2
2
3
3
折
钝角三角形
·
3
2
3
1
拼
∠1+∠2+∠3=180°
锐角三角形
∠1+∠2+∠3=180°
拼
2
1
3
3
直角三角形
拼
3
2
1
3
∠1+∠2+∠3=180°
钝角三角形
任意三角形的内角和都是180°
结论:
A、90°
B、比90°大
C、可能等于90°,大于90°或小于90°
D、还是180°
1、把一个三角形从一个顶点用一条
直线分成两个三角形,其中一个三角形
的内角和( )
D
1
2
3
4
5
6
2、一块三角尺的内角和是180度,用两块完全
一样的三角尺拼成一个三角形,这个三角形
的内角和是360度?
一块三角尺的内角和是180度,用两块完全
一样的三角尺拼成一个三角形,这个三角形
的内角和( )。
180°
2
1
3
3、三角形中,∠1=750,∠2=390,
求∠3的度数
180 —75 —39
=105 —39
=660
180 —(75 +39 )
=180 —114
=660
答:∠3是660
1800—750—390
=1050—390
=660
1800—(750+390)
=1800—1140
=660
4、想一想:在一个直角三角形中,
已知一个锐角是52度,能求出
另一个锐角是多少度吗?
1800—900—520
=900—520
=380
1800—(900+520)
=1800—1420
=380
52°
90°
答:另一个锐角是
52°
5、(1)∠1=30° ∠2=50° ∠3= ( )
这是( )三角形
(2)∠1=50° ∠3=40° ∠2= ( )
这是( )三角形
(3)∠2=70° ∠3=30° ∠1= ( )
这是( )三角形
填一填
100°
90°
80°
钝角
直角
锐角
等腰三角形的两个底角相等。
等边三角形的三个角相等,每个角都是60°。
6、如图,在等腰三角形中,其中底角∠1=65 ,则顶角
∠2=( ).
50°
180 - 65 ×2
=180 -130
=50
2
3
1
65
65
已知底角
7、三角形中,∠1=300,∠2=∠3,求∠3
1
2
3
(1800—300 )÷2
= 1500÷2
= 750
答:∠3是750
30
已知顶角
8、一个等腰三角形,它的一个角的度数是800,求另外两个角的度数。
当80 是顶角时,
(1800—800 )÷2
= 1000÷2
= 500
答:另外两个角是500和500或者800 和200
80
80
80
当80 是底角时,
1800—800—800
= 1000—800
= 200
9、一个等腰三角形,它的一个角的度数是1000,求另外两个角的度数。
100 是顶角
(1800—1000 )÷2
= 800÷2
= 400
答:另外两个角都是400
100
100
100
10、如图,在直角三角形中∠1=35 ,
求∠2=( ),∠3=( ).
1
2
3
55°
125°
∠2 =180 - 90 - ∠1
∠3=180 - ∠2
提示:
帕斯卡(BlaisePascal,1623~1662) ,法国数学家、物理学家、近代概率论的奠基者。早在300多年前这位法国著名的科学家就已经发现了任何三角形的内角和是180°,而他当时才12岁。
三角形的内角和
