24.4 第1课时 弧长和扇形面积公式 课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案)
文档属性
| 名称 | 24.4 第1课时 弧长和扇形面积公式 课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 517.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 08:52:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册课堂同步练
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积公式
要点梳理
1. 半径为R的圆的周长为 ,所以1°的圆心角所对的弧长为 ,所以n°的圆心角所对的弧长 .
2. 由组成圆心角的 和圆心角所对的 所围成的图形叫做扇形.
3. 半径为R的圆的面积为 ,所以1°的圆心角所对的扇形面积为 ,所以圆心角为n°的扇形面积为 .
4. 半径为R,弧长为l的扇形面积为 .
基础过关练
1. 一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
A.300° B.150° C.120° D.75°
2. 如图,☉O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧的长等于( )
A. B. C. D.
3. 如图,正方形ABCD内接于半径为2的☉O,则图中阴影部分的面积为( )
A.π+1 B.π+2 C.π-1 D.π-2
4. 一个扇形的圆心角为100°,面积为15πcm2,则此扇形的半径长为 cm.
5. 如图,已知扇形OAB的圆心角为60°,扇形的面积为为6π,则该扇形的弧长为 .
6. 一个扇形的半径为3cm,弧长为2πcm,则此扇形的面积为 cm2.(用含π的式子表示)
7. 一个扇形的面积为12πcm2,它的圆心角为120°,求这个扇形的半径和弧长.
强化提升练
8. 如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径的长为( )
A.π B.2π C.4π D.8π
9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为,则图中阴影部分的面积是( )
A. B. C.- D.
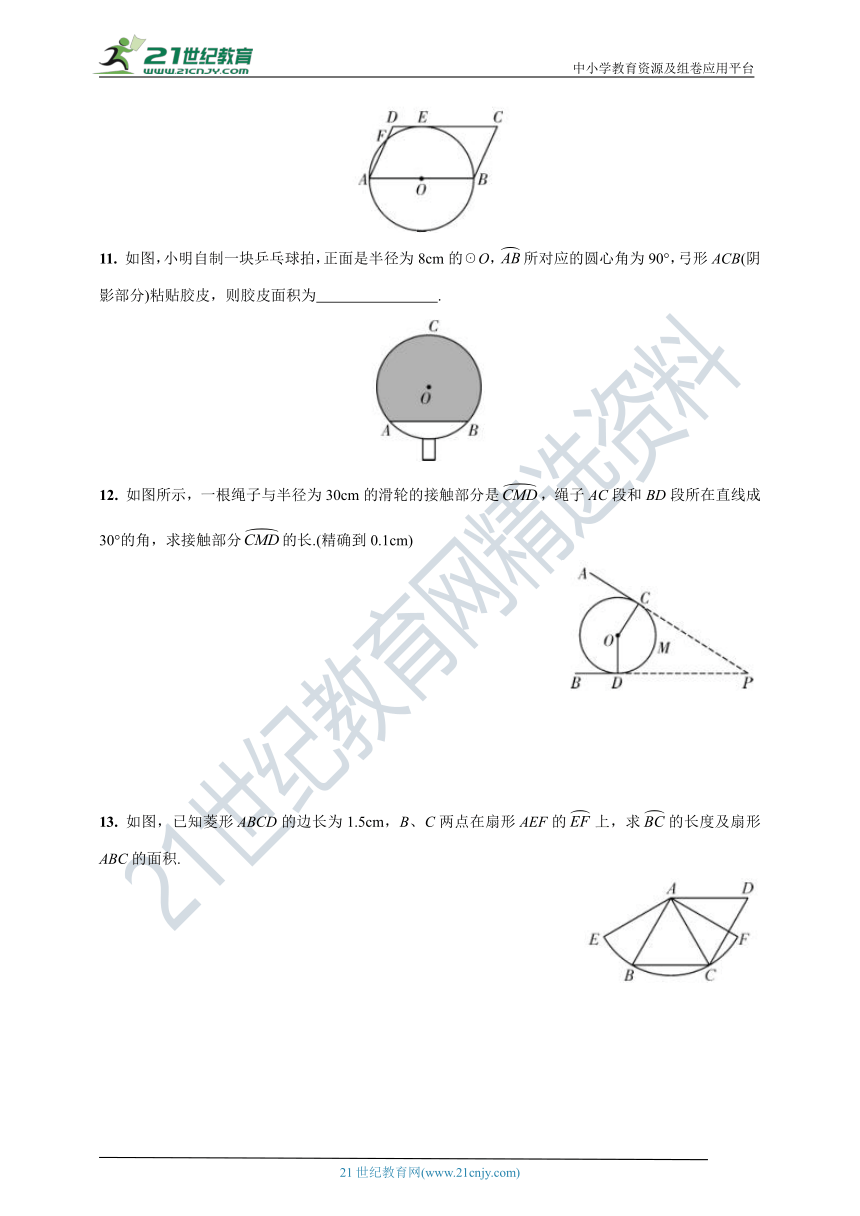
10. 如图,在 ABCD中,AB为☉O的直径,☉O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为 .
11. 如图,小明自制一块乒乓球拍,正面是半径为8cm的☉O,所对应的圆心角为90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为 .
12. 如图所示,一根绳子与半径为30cm的滑轮的接触部分是,绳子AC段和BD段所在直线成30°的角,求接触部分的长.(精确到0.1cm)
13. 如图,已知菱形ABCD的边长为1.5cm,B、C两点在扇形AEF的上,求的长度及扇形ABC的面积.
14. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D.若OA=2,求阴影部分的面积.
延伸拓展练
15. 如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处,再将线段AF绕点F顺时针旋转90°得线段FG,连接EF、CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
参 考 答 案
要点梳理
1. 2πR l= 2. 两条半径 弧 3. πR2 S扇形= 4. S扇形=lR
基础过关练
1. B 2. A 3. D
4. 3
5. 2π
6. 3π
7. 解:由S扇形=πR2,得12π=πR2,∴R2=36,∵R>0,∴R=6,由S扇形=lR得,12π=×l×6,解得l=4π. 答:这个扇形的半径为6cm,弧长为4πcm.
强化提升练
8. B 9. A
10. π
11. (32+48π)cm2
12. 解:∴∠P=30°,∴∠COD=150°,∴的长为=25π≈78.5(cm).
13. 解:∵菱形ABCD的边长为1.5cm,∴扇形的半径R=1.5cm,AB=BC=AC=1.5cm.∴△ABC是等边三角形,∴∠BAC=60°.∴的长l==(cm),S扇形ABC==π(cm2).
14. 解:连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE==π. ∴S阴影=S扇形AOB-S扇形COD-(S扇形AOE-S△COE)=--(π-×1×=π-π+=π+.
延伸拓展练
15. (1)证明:∵四边形ABCD是正方形,∴AB=BC=AD=2,∠ABC=90°,∵△ABF≌△CBE,∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,∴∠AFB+∠FAB=90°,∵∠AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC∥FG,∵AF=EC,AF=FG,∴EC=FG,∴四边形EFGC是平行四边形,∴EF∥CG.
(2)解:∵△ABF≌△CBE,∴FB=BE=AB=1,∴AF==,在△FEC和△CGF中,∵EC=FG,∠ECF=∠GFC,FC=CF,∴△FEC≌△CGF,∴S△FEC=S△CGF,∴S阴影=S扇形BAC+S△ABF+S△FGC-S扇形FAG=+×2×1+×(1+2)×1-=-π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级上册课堂同步练
第二十四章 圆
24.4 弧长和扇形面积
第1课时 弧长和扇形面积公式
要点梳理
1. 半径为R的圆的周长为 ,所以1°的圆心角所对的弧长为 ,所以n°的圆心角所对的弧长 .
2. 由组成圆心角的 和圆心角所对的 所围成的图形叫做扇形.
3. 半径为R的圆的面积为 ,所以1°的圆心角所对的扇形面积为 ,所以圆心角为n°的扇形面积为 .
4. 半径为R,弧长为l的扇形面积为 .
基础过关练
1. 一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
A.300° B.150° C.120° D.75°
2. 如图,☉O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧的长等于( )
A. B. C. D.
3. 如图,正方形ABCD内接于半径为2的☉O,则图中阴影部分的面积为( )
A.π+1 B.π+2 C.π-1 D.π-2
4. 一个扇形的圆心角为100°,面积为15πcm2,则此扇形的半径长为 cm.
5. 如图,已知扇形OAB的圆心角为60°,扇形的面积为为6π,则该扇形的弧长为 .
6. 一个扇形的半径为3cm,弧长为2πcm,则此扇形的面积为 cm2.(用含π的式子表示)
7. 一个扇形的面积为12πcm2,它的圆心角为120°,求这个扇形的半径和弧长.
强化提升练
8. 如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径的长为( )
A.π B.2π C.4π D.8π
9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为,则图中阴影部分的面积是( )
A. B. C.- D.
10. 如图,在 ABCD中,AB为☉O的直径,☉O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则的长为 .
11. 如图,小明自制一块乒乓球拍,正面是半径为8cm的☉O,所对应的圆心角为90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为 .
12. 如图所示,一根绳子与半径为30cm的滑轮的接触部分是,绳子AC段和BD段所在直线成30°的角,求接触部分的长.(精确到0.1cm)
13. 如图,已知菱形ABCD的边长为1.5cm,B、C两点在扇形AEF的上,求的长度及扇形ABC的面积.
14. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D.若OA=2,求阴影部分的面积.
延伸拓展练
15. 如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处,再将线段AF绕点F顺时针旋转90°得线段FG,连接EF、CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
参 考 答 案
要点梳理
1. 2πR l= 2. 两条半径 弧 3. πR2 S扇形= 4. S扇形=lR
基础过关练
1. B 2. A 3. D
4. 3
5. 2π
6. 3π
7. 解:由S扇形=πR2,得12π=πR2,∴R2=36,∵R>0,∴R=6,由S扇形=lR得,12π=×l×6,解得l=4π. 答:这个扇形的半径为6cm,弧长为4πcm.
强化提升练
8. B 9. A
10. π
11. (32+48π)cm2
12. 解:∴∠P=30°,∴∠COD=150°,∴的长为=25π≈78.5(cm).
13. 解:∵菱形ABCD的边长为1.5cm,∴扇形的半径R=1.5cm,AB=BC=AC=1.5cm.∴△ABC是等边三角形,∴∠BAC=60°.∴的长l==(cm),S扇形ABC==π(cm2).
14. 解:连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE==π. ∴S阴影=S扇形AOB-S扇形COD-(S扇形AOE-S△COE)=--(π-×1×=π-π+=π+.
延伸拓展练
15. (1)证明:∵四边形ABCD是正方形,∴AB=BC=AD=2,∠ABC=90°,∵△ABF≌△CBE,∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,∴∠AFB+∠FAB=90°,∵∠AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC∥FG,∵AF=EC,AF=FG,∴EC=FG,∴四边形EFGC是平行四边形,∴EF∥CG.
(2)解:∵△ABF≌△CBE,∴FB=BE=AB=1,∴AF==,在△FEC和△CGF中,∵EC=FG,∠ECF=∠GFC,FC=CF,∴△FEC≌△CGF,∴S△FEC=S△CGF,∴S阴影=S扇形BAC+S△ABF+S△FGC-S扇形FAG=+×2×1+×(1+2)×1-=-π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
