平行四边形及其性质[下学期]
文档属性
| 名称 | 平行四边形及其性质[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-17 00:00:00 | ||
图片预览



文档简介
课件12张PPT。平行四边形及其性质问题一:
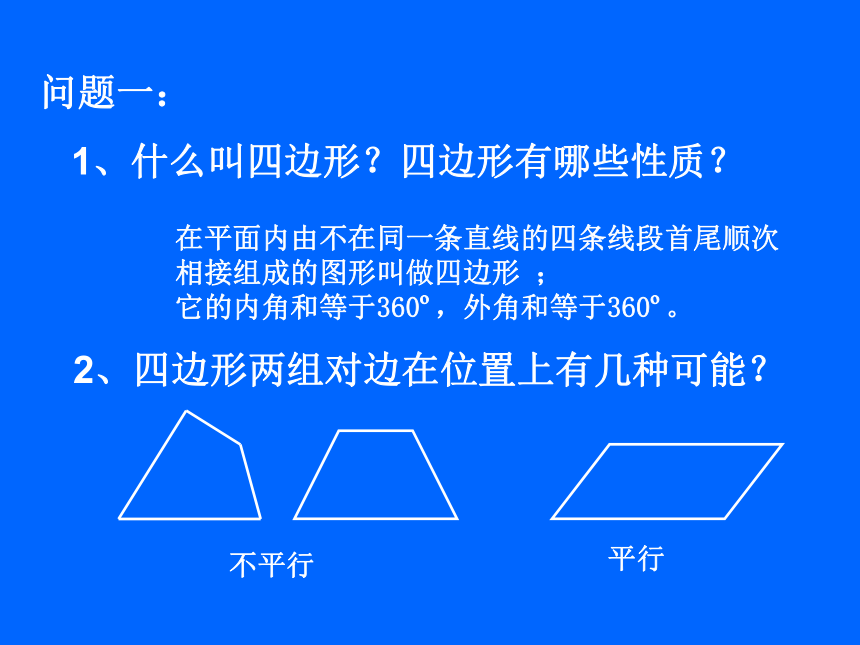
1、什么叫四边形?四边形有哪些性质?2、四边形两组对边在位置上有几种可能? 在平面内由不在同一条直线的四条线段首尾顺次
相接组成的图形叫做四边形 ;
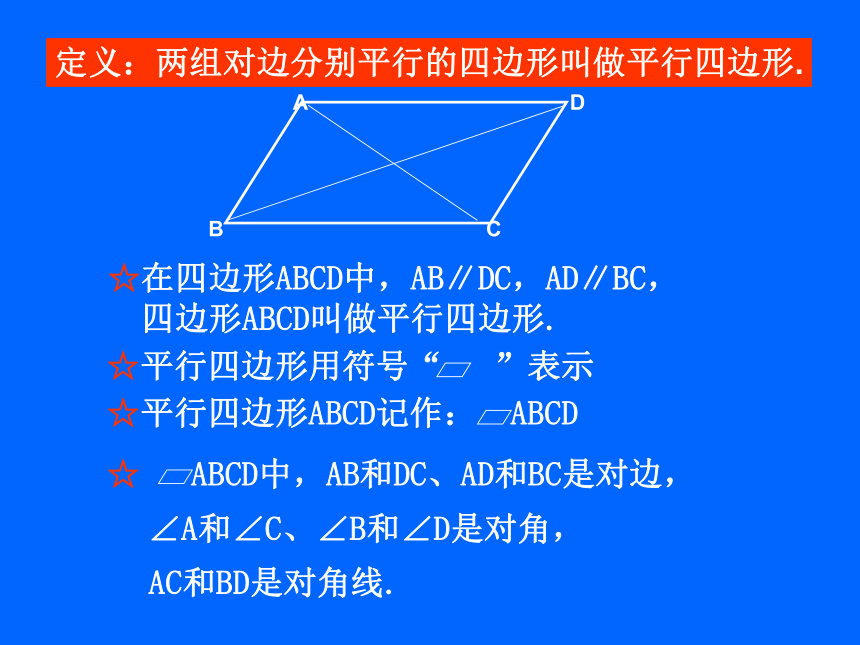
它的内角和等于360o,外角和等于360o。不平行平行定义:两组对边分别平行的四边形叫做平行四边形.☆在四边形ABCD中,AB∥DC,AD∥BC,
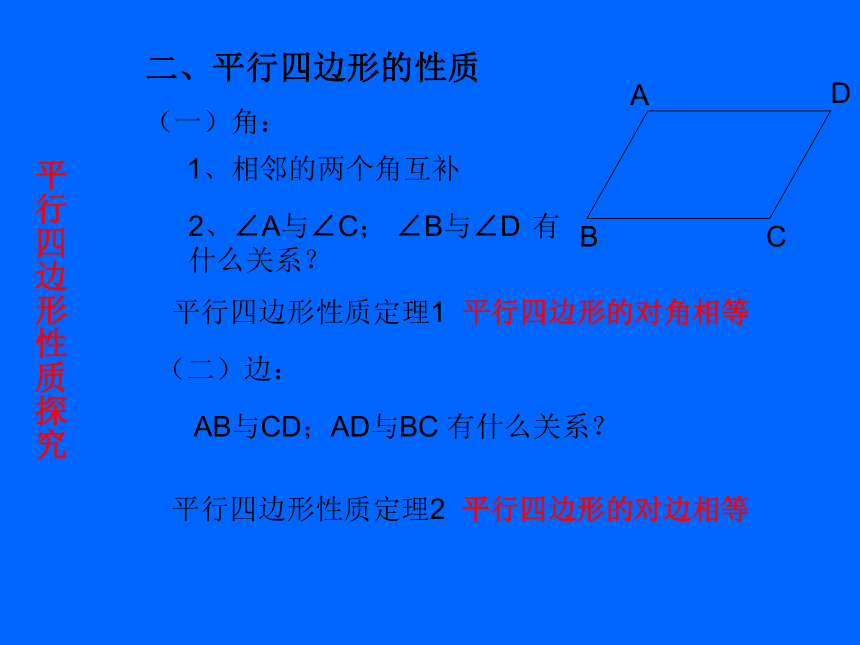
四边形ABCD叫做平行四边形.∠A和∠C、∠B和∠D是对角, 平行四边形性质探究(一)角:1、相邻的两个角互补2、∠A与∠C; ∠B与∠D 有
什么关系?平行四边形性质定理1 平行四边形的对角相等(二)边:AB与CD;AD与BC 有什么关系?平行四边形性质定理2 平行四边形的对边相等二、平行四边形的性质1、平行四边形的内角和是 ,外角和是 . 练习:∠C=130o,∠D=50o,∠A=130o2a+2b例2:如图,已知:DE∥BA,EF∥CB,FD∥AC
求证:(1)∠ABC=∠E
∠CAB=∠D
∠BCA=∠F
(2)△ABC的顶点分别是△EFD各边的中点.证明:
(1)∵ DE∥BA,EF∥CB,
∴ 四边形ABCE是平行四边形
∴ ∠ABC=∠E(平行四边形的对角相等)
同理∠CAB=∠D,∠BCA=∠F.
⑵ 由⑴证得四边形ABCE是平行四边形.
同理,四边形ABDC是平行四边形。
∴ AB=EC,AB=DC(平行四边形的对边相等)
∴ EC=DC
同理,EA=FA,DB=FB
∴ △ABC的顶点分别是△EFD各边的中点.小 结2、平行四边形的性质:1、平行四边形的定义:两组对边分别平行的四边形平行四边形的对角相等
平行四边形的对边相等注意、平行四边形的应用中要注意一个隐含条件:平行四边形的邻角互补。
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示?拼一拼小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。再见
1、什么叫四边形?四边形有哪些性质?2、四边形两组对边在位置上有几种可能? 在平面内由不在同一条直线的四条线段首尾顺次
相接组成的图形叫做四边形 ;
它的内角和等于360o,外角和等于360o。不平行平行定义:两组对边分别平行的四边形叫做平行四边形.☆在四边形ABCD中,AB∥DC,AD∥BC,
四边形ABCD叫做平行四边形.∠A和∠C、∠B和∠D是对角, 平行四边形性质探究(一)角:1、相邻的两个角互补2、∠A与∠C; ∠B与∠D 有
什么关系?平行四边形性质定理1 平行四边形的对角相等(二)边:AB与CD;AD与BC 有什么关系?平行四边形性质定理2 平行四边形的对边相等二、平行四边形的性质1、平行四边形的内角和是 ,外角和是 . 练习:∠C=130o,∠D=50o,∠A=130o2a+2b例2:如图,已知:DE∥BA,EF∥CB,FD∥AC
求证:(1)∠ABC=∠E
∠CAB=∠D
∠BCA=∠F
(2)△ABC的顶点分别是△EFD各边的中点.证明:
(1)∵ DE∥BA,EF∥CB,
∴ 四边形ABCE是平行四边形
∴ ∠ABC=∠E(平行四边形的对角相等)
同理∠CAB=∠D,∠BCA=∠F.
⑵ 由⑴证得四边形ABCE是平行四边形.
同理,四边形ABDC是平行四边形。
∴ AB=EC,AB=DC(平行四边形的对边相等)
∴ EC=DC
同理,EA=FA,DB=FB
∴ △ABC的顶点分别是△EFD各边的中点.小 结2、平行四边形的性质:1、平行四边形的定义:两组对边分别平行的四边形平行四边形的对角相等
平行四边形的对边相等注意、平行四边形的应用中要注意一个隐含条件:平行四边形的邻角互补。
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?从拼图可以得到什么启示?拼一拼小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。再见
