19.1.2平行四边形的判定(一)[下学期]
文档属性
| 名称 | 19.1.2平行四边形的判定(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-18 00:00:00 | ||
图片预览



文档简介
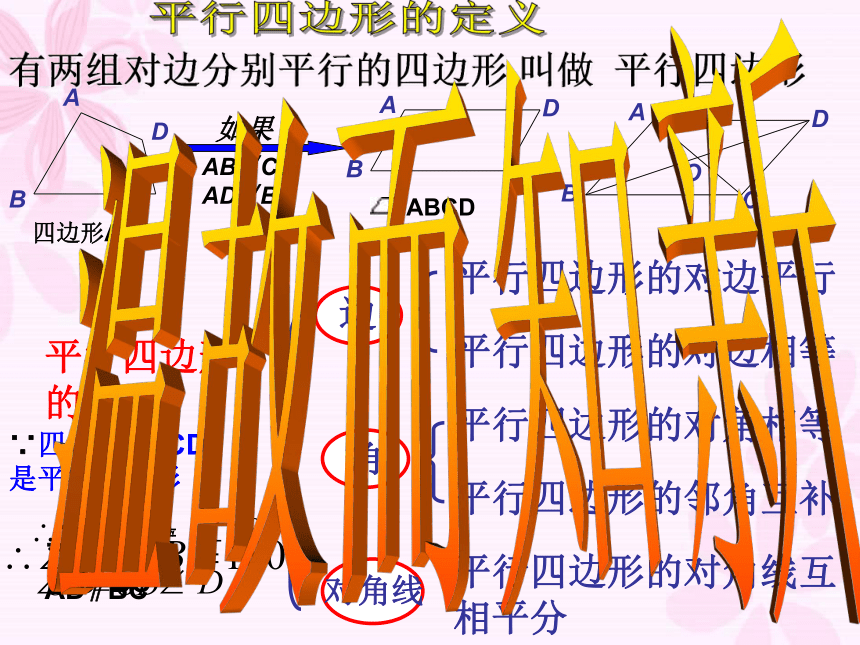
课件19张PPT。平行四边形的判定(一)有两组对边分别平行的四边形叫做平行四边形平行四边形的定义平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分∵四边形ABCD 是平行四边形∴AB=CD
AD=BC∴AB∥CD
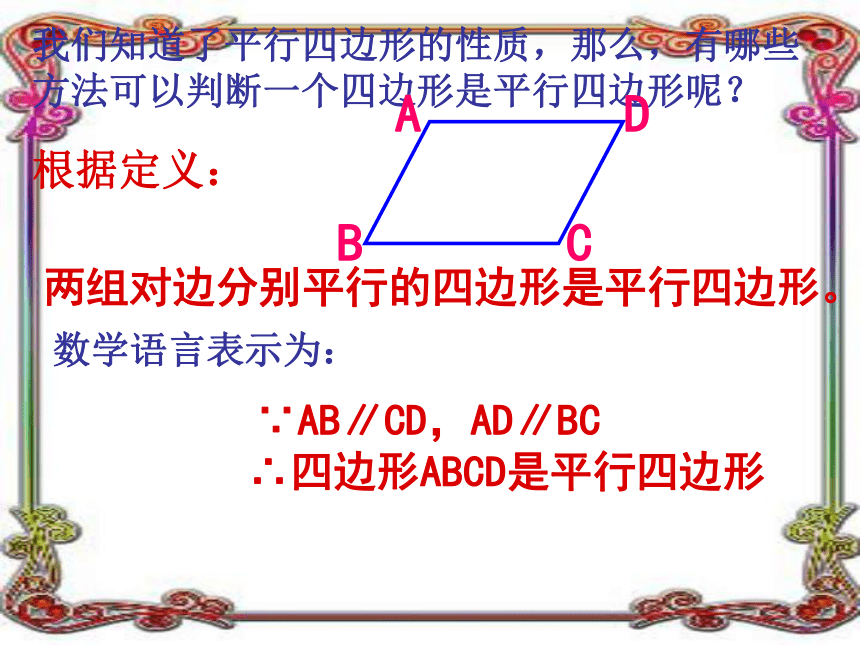
AD∥BC温故而知新我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢? 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形 数学语言表示为:根据定义:平行四边形的判定方法小结两组对边分别平行的
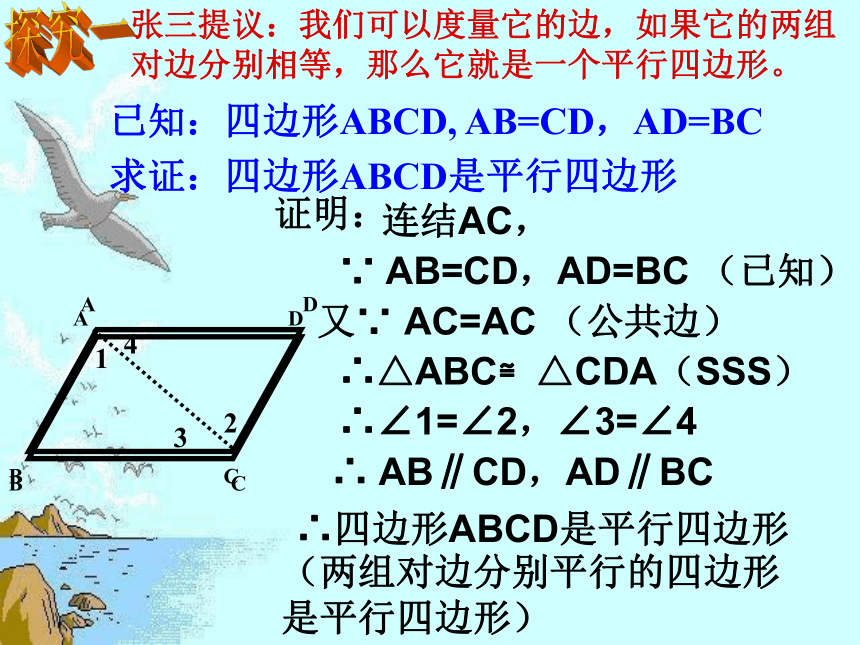
四边形是平行四边形。方法 一还有其他方法吗?老师说下列四边形是平行四边形,你相信吗?制造悬念已知:四边形ABCD, AB=CD,AD=BC
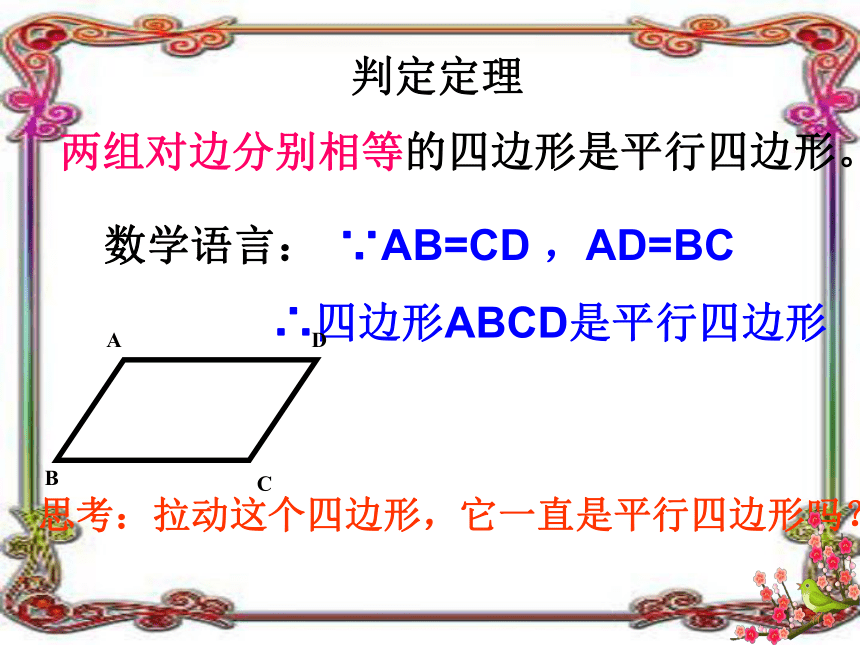
求证:四边形ABCD是平行四边形张三提议:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形。连结AC,∵ AB=CD,AD=BC (已知)又∵ AC=AC (公共边)∴△ABC≌△CDA(SSS)∴∠1=∠2,∠3=∠4∴ AB∥CD,AD∥BC ∴四边形ABCD是平行四边形证明:探究一(两组对边分别平行的四边形是平行四边形)两组对边分别相等的四边形是平行四边形。判定定理数学语言: ∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形 思考:拉动这个四边形,它一直是平行四边形吗? 平行四边形的判定方法小结 两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。方法 一还有其他方法吗?方法 二李四提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形已知:四边形ABCD,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形证明:∵∠A=∠C,∠B=∠D(已知)又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD∴四边形ABCD是平行四边形探究二平行四边形判定定理 两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形数学语言表示为:平行四边形的判定方法小结 两组对角分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。方法 一还有其他方法吗?方法 二方法 三 王五说:“我可以不用任何作图工具,只要两
条细绳就能判断它是不是平行四边形。”
只见王五用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,王五高兴地说:“这的确是个平行四边形!”你认为王五的做法有根据吗?O对角线互相平分探究三证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是 平行四边形
(两组对边分别平行的四边形是平行四边形)DABCO1234∴ ∠3 = ∠4已知:四边形ABCD的对角线AC、BD 相交于 点O,并且AO = CO ,BO = DO 。求证:四边形ABCD是平行四边形。对角线互相平分的四边形是平行四边形。判定定理数学语言:∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形平行四边形的判定方法小结 两条对角线互相平分的四边形是 平行四边形。 两组对角分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。方法 一方法 二方法 三方法 四老师说下列四边形是平行四边形,你相信吗?请说出理由 两组对边分别相等的四边形是平行四边形 两组对角分别相等的四边形是平行四边形 两条对角线互相平分的四边形是 平行四边形。 现在来看看
仔细哟例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.我的收获
我的困惑课堂小结平行四边形的判定方法两条对角线互相平分的四边形是平行四边形。 两组对角分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。大显身手例1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE∥DF
AD=BC∴AB∥CD
AD∥BC温故而知新我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢? 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形 数学语言表示为:根据定义:平行四边形的判定方法小结两组对边分别平行的
四边形是平行四边形。方法 一还有其他方法吗?老师说下列四边形是平行四边形,你相信吗?制造悬念已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形张三提议:我们可以度量它的边,如果它的两组对边分别相等,那么它就是一个平行四边形。连结AC,∵ AB=CD,AD=BC (已知)又∵ AC=AC (公共边)∴△ABC≌△CDA(SSS)∴∠1=∠2,∠3=∠4∴ AB∥CD,AD∥BC ∴四边形ABCD是平行四边形证明:探究一(两组对边分别平行的四边形是平行四边形)两组对边分别相等的四边形是平行四边形。判定定理数学语言: ∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形 思考:拉动这个四边形,它一直是平行四边形吗? 平行四边形的判定方法小结 两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。方法 一还有其他方法吗?方法 二李四提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形已知:四边形ABCD,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形证明:∵∠A=∠C,∠B=∠D(已知)又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD∴四边形ABCD是平行四边形探究二平行四边形判定定理 两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形数学语言表示为:平行四边形的判定方法小结 两组对角分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。方法 一还有其他方法吗?方法 二方法 三 王五说:“我可以不用任何作图工具,只要两
条细绳就能判断它是不是平行四边形。”
只见王五用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,王五高兴地说:“这的确是个平行四边形!”你认为王五的做法有根据吗?O对角线互相平分探究三证明:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是 平行四边形
(两组对边分别平行的四边形是平行四边形)DABCO1234∴ ∠3 = ∠4已知:四边形ABCD的对角线AC、BD 相交于 点O,并且AO = CO ,BO = DO 。求证:四边形ABCD是平行四边形。对角线互相平分的四边形是平行四边形。判定定理数学语言:∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形平行四边形的判定方法小结 两条对角线互相平分的四边形是 平行四边形。 两组对角分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。方法 一方法 二方法 三方法 四老师说下列四边形是平行四边形,你相信吗?请说出理由 两组对边分别相等的四边形是平行四边形 两组对角分别相等的四边形是平行四边形 两条对角线互相平分的四边形是 平行四边形。 现在来看看
仔细哟例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.我的收获
我的困惑课堂小结平行四边形的判定方法两条对角线互相平分的四边形是平行四边形。 两组对角分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形两组对边分别平行的四边形是平行四边形。大显身手例1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE∥DF
