北师大版数学七年级下册 1.5平方差公式 课件(共19张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 1.5平方差公式 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 927.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第一章 整式的运算
1.5.1平方差公式
—多种方式融入数学史以渗透德育教育
庄园主巴依老爷与佃户张老汉的故事
一、故事引入
二、平方差公式的证明
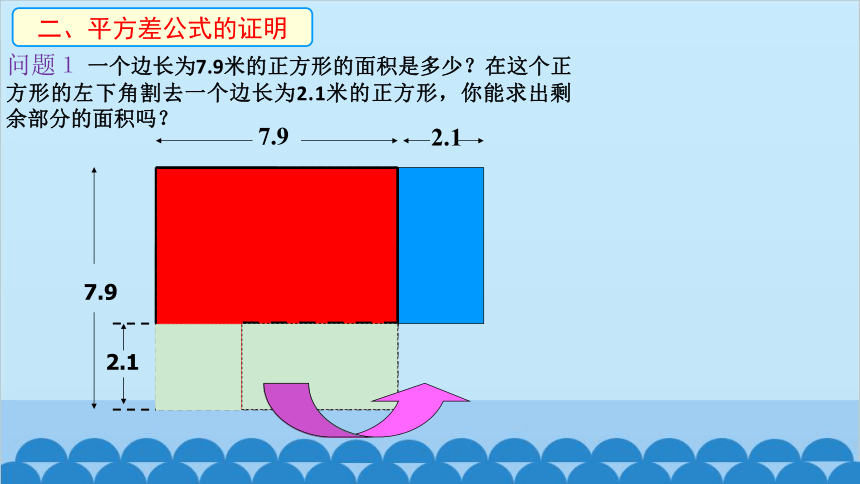
问题1 一个边长为7.9米的正方形的面积是多少?在这个正方形的左下角割去一个边长为2.1米的正方形,你能求出剩余部分的面积吗?
7.9
2.1
7.9
2.1
问题2
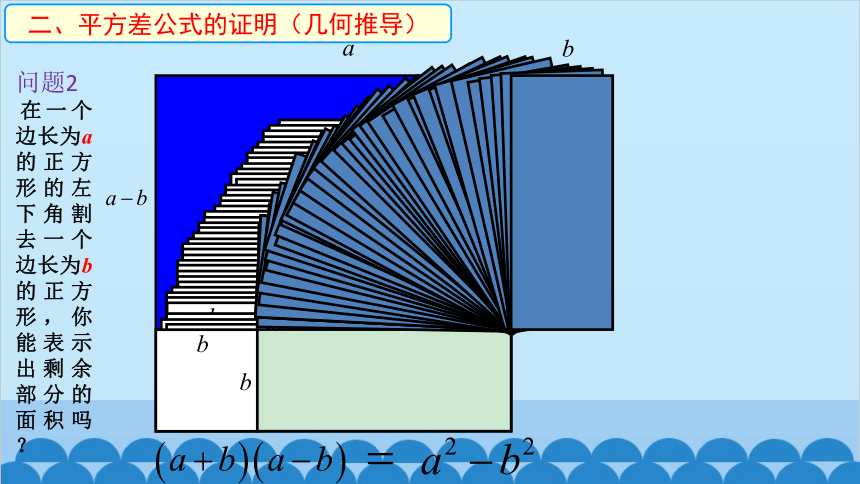
在一个边长为a的正方形的左下角割去一个边长为b的正方形,你能表示出剩余部分的面积吗?
二、平方差公式的证明(几何推导)
(a+b)(a b)=a2 b2
两数和与这两数差的积,等于这两数的平方差.
知识要点
平方差公式:
面积割补的证明方法最早是由我国三国时代的数学家赵爽想出来的。对赵爽的生平人们知之甚少,在《〈周髀算经〉注》的前言里,赵爽说自己“负薪余日,聊观《周髀》”。
赵爽:负薪余日,
聊观《周髀》
赵爽励志故事
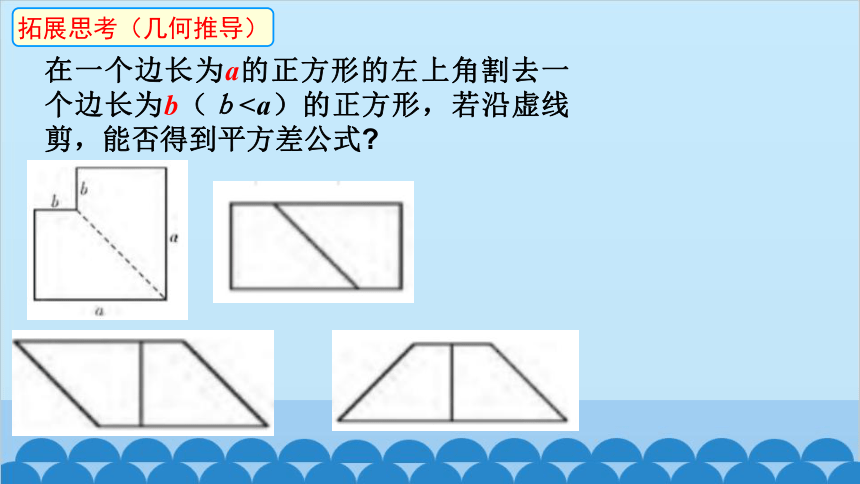
拓展思考(几何推导)
在一个边长为a的正方形的左上角割去一个边长为b(b公式代数推导
(a+b)(a-b) = a2-b2
相同为a
相反为b
三、平方差公式的特征
特
征
(2)a和b是数,单项式或多项式。
(1)一同一反,积等于同方减反方。
巧识:孙悟空大战二郎神:
两个二郎神(二项乘),一同一反,同方战(减)反方。
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
1、填一填:
a
b
=a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a+b)(a-b)
四、平方差公式的应用
2、利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (-2y+x)(2y+x);
(3) (n-m)(-m-n) ; (4) 30.2×29.8
解:(1)原式=52-(6x)2=25-36x2;
(2)原式=x2-(2y)2=x2 - 4y2;
(3)原式=(-m)2-n2=m2-n2.
(4)原式=(30+0.2)×(30-0.2)
=302-0.22=900-0.04=899.96
古希腊数学家欧几里得在《几何原本》中就已经利用几何方法得到上述变形了.
3、利用平方差公式计算:
(1) (2) (ab+8)(ab-8).
解:(1)原式=
(1)原式=(ab)2-82
=a2b2-64.
思考题:
已知两数的和为 20,积为 96,求这两个数。
解法:设两数分别为10+x和10-x,则(10+x)(10-x)=96,即
102-x2 =96,故100-x2 =96,
故x2 =4, x=2.于是,所求两数分别为12和8.
从前,有一个狡猾的庄园主——巴依老爷,巴依老爷又开始数他的金币了:“金币呀,你能否再多点呀” ,今天是张老汉来还钱的日子,我得好好想想。一会,张老汉来了:“巴依老爷,天旱收成不好,你再宽限几天吧。”“那怎么行?”“再宽限几天吧。”“这样吧,把你那块边长为a的正方形地一边增加5米,另一边减少5米,变成长方形继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉一听觉得好像没有吃亏,就答应了. 同学们,你们觉得张老汉吃亏没有,为什么?
结论:两个多边形周长相等时,其面积不一定相等。
练一练
(2)(填空) (2x-3y)( )=9y2 –4x2
-2x-3y
(3)计算: (a-b)(-a-b)
或 解:原式=-(a-b)(a+b)
=-(a2-b2)
=b2-a2
解:原式=(-b+a)(-b-a)
=(-b)2-a2
=b2-a2
D
课堂小结
分享你的收获,交流你的困惑。
通过本节课的学习,你有哪些收获?
(1)说说应用平方差公式的条件,以及注意事项。
(2)你觉得平方差公式的数学历史对你的学习有帮助吗? 如果有帮助,主要是哪方面的?
(3)本节课你记忆最深刻的是哪个环节,为什么?
我们可不能像佃户张老汉那样被表面现象所迷惑,要开拓自己丢番图式的智慧头脑;像赵爽那样挤一挤,时间总是有的,好好利用时间学习知识,利用所学知识解决一些日常生活中的问题,才能透过现象看本质;做人我们可不能像庄园主那样,要踏踏实实做人,诚实守信…
赠言:
课后作业
1) 位置变化: (a+b) (–b+a) =________.
2) 符号变化: (-a–b) (a–b)=_________.
3) 系数变化:(2a+3b)(2a-3b)=_________.
4) 指数变化:( a3+b2 )(a3 –b2 )=________.
5) 项数变化: (a+2b+c) (a+2b-c) = .
(1)(一题多变)平方差公式的常见变形:
谢谢!
第一章 整式的运算
1.5.1平方差公式
—多种方式融入数学史以渗透德育教育
庄园主巴依老爷与佃户张老汉的故事
一、故事引入
二、平方差公式的证明
问题1 一个边长为7.9米的正方形的面积是多少?在这个正方形的左下角割去一个边长为2.1米的正方形,你能求出剩余部分的面积吗?
7.9
2.1
7.9
2.1
问题2
在一个边长为a的正方形的左下角割去一个边长为b的正方形,你能表示出剩余部分的面积吗?
二、平方差公式的证明(几何推导)
(a+b)(a b)=a2 b2
两数和与这两数差的积,等于这两数的平方差.
知识要点
平方差公式:
面积割补的证明方法最早是由我国三国时代的数学家赵爽想出来的。对赵爽的生平人们知之甚少,在《〈周髀算经〉注》的前言里,赵爽说自己“负薪余日,聊观《周髀》”。
赵爽:负薪余日,
聊观《周髀》
赵爽励志故事
拓展思考(几何推导)
在一个边长为a的正方形的左上角割去一个边长为b(b
(a+b)(a-b) = a2-b2
相同为a
相反为b
三、平方差公式的特征
特
征
(2)a和b是数,单项式或多项式。
(1)一同一反,积等于同方减反方。
巧识:孙悟空大战二郎神:
两个二郎神(二项乘),一同一反,同方战(减)反方。
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
1、填一填:
a
b
=a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a+b)(a-b)
四、平方差公式的应用
2、利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (-2y+x)(2y+x);
(3) (n-m)(-m-n) ; (4) 30.2×29.8
解:(1)原式=52-(6x)2=25-36x2;
(2)原式=x2-(2y)2=x2 - 4y2;
(3)原式=(-m)2-n2=m2-n2.
(4)原式=(30+0.2)×(30-0.2)
=302-0.22=900-0.04=899.96
古希腊数学家欧几里得在《几何原本》中就已经利用几何方法得到上述变形了.
3、利用平方差公式计算:
(1) (2) (ab+8)(ab-8).
解:(1)原式=
(1)原式=(ab)2-82
=a2b2-64.
思考题:
已知两数的和为 20,积为 96,求这两个数。
解法:设两数分别为10+x和10-x,则(10+x)(10-x)=96,即
102-x2 =96,故100-x2 =96,
故x2 =4, x=2.于是,所求两数分别为12和8.
从前,有一个狡猾的庄园主——巴依老爷,巴依老爷又开始数他的金币了:“金币呀,你能否再多点呀” ,今天是张老汉来还钱的日子,我得好好想想。一会,张老汉来了:“巴依老爷,天旱收成不好,你再宽限几天吧。”“那怎么行?”“再宽限几天吧。”“这样吧,把你那块边长为a的正方形地一边增加5米,另一边减少5米,变成长方形继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉一听觉得好像没有吃亏,就答应了. 同学们,你们觉得张老汉吃亏没有,为什么?
结论:两个多边形周长相等时,其面积不一定相等。
练一练
(2)(填空) (2x-3y)( )=9y2 –4x2
-2x-3y
(3)计算: (a-b)(-a-b)
或 解:原式=-(a-b)(a+b)
=-(a2-b2)
=b2-a2
解:原式=(-b+a)(-b-a)
=(-b)2-a2
=b2-a2
D
课堂小结
分享你的收获,交流你的困惑。
通过本节课的学习,你有哪些收获?
(1)说说应用平方差公式的条件,以及注意事项。
(2)你觉得平方差公式的数学历史对你的学习有帮助吗? 如果有帮助,主要是哪方面的?
(3)本节课你记忆最深刻的是哪个环节,为什么?
我们可不能像佃户张老汉那样被表面现象所迷惑,要开拓自己丢番图式的智慧头脑;像赵爽那样挤一挤,时间总是有的,好好利用时间学习知识,利用所学知识解决一些日常生活中的问题,才能透过现象看本质;做人我们可不能像庄园主那样,要踏踏实实做人,诚实守信…
赠言:
课后作业
1) 位置变化: (a+b) (–b+a) =________.
2) 符号变化: (-a–b) (a–b)=_________.
3) 系数变化:(2a+3b)(2a-3b)=_________.
4) 指数变化:( a3+b2 )(a3 –b2 )=________.
5) 项数变化: (a+2b+c) (a+2b-c) = .
(1)(一题多变)平方差公式的常见变形:
谢谢!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
