人教版数学八年级上册14.2.2完全平方公式 教案
文档属性
| 名称 | 人教版数学八年级上册14.2.2完全平方公式 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 171.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 09:49:29 | ||
图片预览



文档简介
14.2.2 完全平方公式
一、教学目标
【知识与技能】
1.会推导完全平方公式,并能运用公式进行简单的运算.
2. 掌握乘法公式的结构特征及公式的含义,理解添括号法则,会正确地添括号运用这些公式进行计算.
【过程与方法】
1.经历利用多项式与多项式的乘法以及幂的意义,推导出完全平方公式的过程.
2. 通过探索和理解乘法公式,感受乘法公式从一般到特殊的认知过程,拓展思维空间.
【情感、态度与价值观】
1. 通过完全平方公式的应用,体会公式中字母的含义,渗透整体、数形结合、类比的数学思想.
2. 培养良好的分析思想和与人合作的习惯,体会数学的重要价值.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
1.完全平方公式的推导过程,结构特点,几何解释;
2.完全平方公式的应用.
3. 利用添括号法则灵活应用乘法公式进行运算.
【教学难点】
1. 完全平方公式的特点及整体思想的渗透.
2. 根据式子特点灵活添加括号,使其符合乘法公式特点.
五、课前准备
教师:课件、直尺、矩形、正方形结构图等。
学生:三角尺、练习本、钢笔或圆珠笔、铅笔、直尺。
六、教学过程
(一)导入新课
现有如图所示的三种规格的硬纸片各若干张,请你根据二次三项式a2+2ab+b2,选取相应种类和数量的硬纸片,拼出一个正方形,并探究所拼出的正方形的代数意义.(出示课件2)
(二)探索新知
1.设计问题,探究完全平方公式
教师问1:根据前面所学知识,思考下面这个题目该怎么做?(出示课件4)
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
学生回答:
(1) 直接求:总面积=(a+b)(a+b);
(2) 间接求:总面积=a2+ab+ab+b2
教师问2:你发现了什么?:
学生回答:
(a+b)2=a2+2ab+b2
教师问3:计算下列多项式的积,你能发现什么规律?(出示课件5)
(1) (p+1)2=(p+1)(p+1)=
(2) (m+2)2=(m+2)(m+2)=
(3) (p–1)2=(p–1)(p–1)= .
(4) (m–2)2=(m–2)(m–2)= .
学生计算结果如下:
(1)p2+2p+1;(2)m2+4m+4;(3)p2–2p+1;(4)m2–4m+4。
学生交流并且讨论后回答:两个数和的平方,等于这两个数的平方和加上这两个数乘积的两倍;两个数差的平方,等于这两个数的平方和减去这两个数乘积的两倍.
教师问4:根据你发现的规律,你能写出下列式子的答案吗?
学生回答:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.
教师总结:(出示课件6)
完全平方公式
文字叙述:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
符号叙述:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.
简记为:
“首平方,尾平方,积的2倍放中央”
教师问5:怎么验证这一规律呢?
学生回答:可以通过计算来验证.(学生小组内独立完成)
教师问6:你能根据下面图形的面积说明完全平方公式吗 (出示课件7)
学生讨论后得出:就是如何验证(a+b)2=a2+2ab+b2
师生共同解答如下:图中可以看出大正方形的边长是a+b,还可以看出大正方形是由两个小正方形和两个矩形组成,所以大正方形的面积等于这四个图形的面积之和.阴影部分的正方形边长是a,所以它的面积是a2.另一个小正方形的边长是b,所以它的面积是b2.另外两个矩形的长都是a,宽都是b,所以每个矩形的面积都是ab;大正方形的边长是a+b,其面积是(a+b)2.于是就可以得出:(a+b)2=a2+2ab+b2.
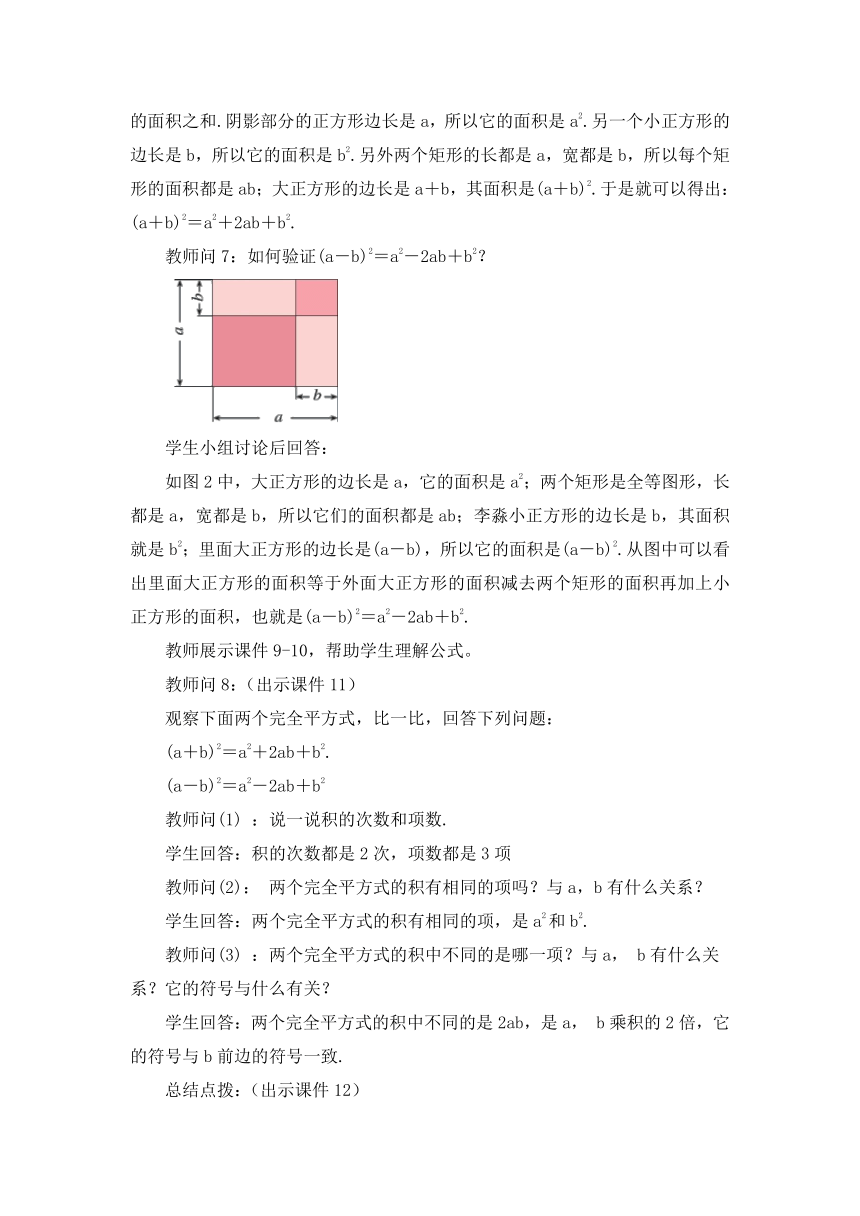
教师问7:如何验证(a-b)2=a2-2ab+b2?
学生小组讨论后回答:
如图2中,大正方形的边长是a,它的面积是a2;两个矩形是全等图形,长都是a,宽都是b,所以它们的面积都是ab;李淼小正方形的边长是b,其面积就是b2;里面大正方形的边长是(a-b),所以它的面积是(a-b)2.从图中可以看出里面大正方形的面积等于外面大正方形的面积减去两个矩形的面积再加上小正方形的面积,也就是(a-b)2=a2-2ab+b2.
教师展示课件9-10,帮助学生理解公式。
教师问8:(出示课件11)
观察下面两个完全平方式,比一比,回答下列问题:
(a+b)2=a2+2ab+b2.
(a-b)2=a2-2ab+b2
教师问(1) :说一说积的次数和项数.
学生回答:积的次数都是2次,项数都是3项
教师问(2): 两个完全平方式的积有相同的项吗?与a,b有什么关系?
学生回答:两个完全平方式的积有相同的项,是a2和b2.
教师问(3) :两个完全平方式的积中不同的是哪一项?与a, b有什么关系?它的符号与什么有关?
学生回答:两个完全平方式的积中不同的是2ab,是a, b乘积的2倍,它的符号与b前边的符号一致.
总结点拨:(出示课件12)
公式特征:
1. 积为二次三项式;
2. 积中两项为两数的平方和;
3. 另一项是两数积的2倍,且与两数中间的符号相同.
4. 公式中的字母a,b可以表示数、单项式和多项式.
例1:运用完全平方公式计算:(出示课件14)
(1)(4m+n)2;(2) (y-)2
师生共同解答如下:
例2:运用完全平方公式计算:(出示课件16)
(1) 1022;(2) 992.
师生共同解答如下:
解:(1) 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
=(100-1)2
=10000 –200+1
=9801.
总结点拨:当一个数具备与整十、整百……相差一个正整数时求它的平方,我们可以通过变形运用完全平方公式进行运算较简便.
例3:已知x–y=6,xy=–8.(出示课件18)
求:(1) x2+y2的值; (2)(x+y)2的值.
师生共同解答如下:
解:(1)∵x–y=6,xy=–8,
(x–y)2=x2+y2–2xy,
∴x2+y2=(x–y)2+2xy
=36 –16=20;
(2)∵x2+y2=20,xy=–8,
∴(x+y)2=x2+y2+2xy
=20 –16=4.
总结点拨:本题要熟练掌握完全平方公式的变式:
x2+y2=(x–y)2+2xy=(x+y)2–2xy,(x–y)2=(x+y)2–4xy.
2.创设情境,探究添括号法则
教师问9:同学们完成下列运算.
(1)4+(5+2); (2)4-(5+2); (3)a+(b+c); (4)a-(b-c).
学生回答:
(1)4+(5+2)=4+5+2=9+2=11;
(2)4-(5+2)=4-5-2=-3;
(3)a+(b+c)=a+b+c;
(4)a-(b-c)=a-b+c.
教师问10:去括号法则是什么呢?.
学生回答:
去括号时,如果括号前是正号,去掉括号后,括号里的每一项都不改变符号;如果括号前是负号,去掉括号后,括号里的各项都改变符号.
也就是说,遇“加”不变,遇“减”都变.
教师问11:把下面两个等式的左右两边反过来,得到什么?(出示课件20)
a+(b+c)=a+b+c; a-(b+c)=a-b-c.
学生回答:
a + b + c = a + ( b + c) ;
a – b - c = a – ( b + c ) .
教师问12:你能总结出添括号法则吗?
学生小结:添括号其实就是把去括号反过来。
也是:遇“加”不变,遇“减”都变.
总结点拨:(出示课件21)
添括号法则是去括号法则反过来得到的,无论是添括号,还是去括号,运算前后代数式的值都保持不变,所以我们可以用去括号法则验证所添括号后的代数式是否正确.
例4:运用乘法公式计算:(出示课件22)
(1) (x+2y–3)(x–2y+3) ; (2) (a+b+c)2.
师生共同解答如下:
解: (1)原式=[x+(2y–3)][x–(2y–3)]
= x2–(2y–3)2
= x2–(4y2–12y+9)
= x2–4y2+12y–9.
(2)原式= [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
(三)课堂练习(出示课件25-28)
1. 运用乘法公式计算(a–2)2的结果是( )
A.a2–4a+4 B.a2–2a+4
C.a2–4 D.a2–4a–4
2.下列计算结果为2ab–a2–b2的是( )
A.(a–b)2 B.(–a–b)2
C.–(a+b)2 D.–(a–b)2
3.运用完全平方公式计算:
(1) (6a+5b)2=_______________;(2) (4x–3y)2=_______________ ;
(3) (2m–1)2 =_______________;(4)(–2m–1)2 =_______________.
4.由完全平方公式可知:32+2×3×5+52=(3+5)2=64,运用这一方法计算:4.3212+8.642×0.679+0.6792=________.
5. 计算:(1)(3a+b–2)(3a–b+2);(2)(x–y–m+n)(x–y+m–n).
6. 若a+b=5,ab=–6, 求a2+b2,a2–ab+b2.
7. 已知x+y=8,x–y=4,求xy.
参考答案:
1.A
2.D
3.(1) 36a2+60ab+25b2;(2)16x2–24xy+9y2;(3)4m2–4m+1;(4)4m2+4m+1
4.25
5. 解:(1)原式=[3a+(b–2)][3a–(b–2)] =(3a)2–(b–2)2
=9a2–b2+4b–4.
(2)原式=[(x–y)–(m–n)][(x–y)+(m–n)]
=(x–y)2–(m–n)2
=x2–2xy+y2–m2+2mn–n2.
6. 解:a2+b2=(a+b)2–2ab=52–2×(–6)=37;
7. 解:∵x+y=8, ∴(x+y)2=64,即x2+y2+2xy=64①;
∵x–y=4, ∴(x–y)2=16,即x2+y2–2xy=16②;
由①–②得4xy=48,∴xy=12.
(四)课堂小结
今天我们学了哪些内容:
1. 完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
2. 添括号法则:遇“加”不变,遇“减”都变.
(五)课前预习
预习下节课(14.3.1)的相关内容。
知道公因式、提公因式法的定义
七、课后作业
1、教材110页练习1,2和教材111页练习1,2
2、如图,长方形ABCD的周长是20 cm,以AB,AD为边分别向外作正方形ABEF和正方形ADGH,若正方形ABEF和正方形ADGH的面积之和为68 cm2,那么长方形ABCD的面积是( )
A.21 cm2 B.16 cm2 C.24 cm2 D.9 cm2
八、板书设计:
九、教学反思:
1. 本节课充分发挥了学生自主学习、探究的能力.从归纳猜想、随堂练习到公式验证、巩固提高,都渗透着从学生自主探索,再到学生与学生之间的合作交流学习,都突出了学生是探索性学习活动的主体这一理念.此外,还充分挖掘本课时教材中的隐含的各种数学思想,在教学中渗透如数形结合思想、换元思想、化归思想,注重培养学生发现问题、解决问题的能力.
2. 本节课是在学方差公式与完全平方公式之后进行的,本课时中的内容不多,但对知识的要求较高,难点也较多,对学生的要求也较高,所以对课堂教学的组织要求就更高.因此在设计活动时,紧紧围绕着乘法公式的形式展开,并根据活动情况不断地变换问题,以问题为核心调动学生参与活动的兴趣与积极性,在每一个教学环节都对学生提出了不同的要求.
一、教学目标
【知识与技能】
1.会推导完全平方公式,并能运用公式进行简单的运算.
2. 掌握乘法公式的结构特征及公式的含义,理解添括号法则,会正确地添括号运用这些公式进行计算.
【过程与方法】
1.经历利用多项式与多项式的乘法以及幂的意义,推导出完全平方公式的过程.
2. 通过探索和理解乘法公式,感受乘法公式从一般到特殊的认知过程,拓展思维空间.
【情感、态度与价值观】
1. 通过完全平方公式的应用,体会公式中字母的含义,渗透整体、数形结合、类比的数学思想.
2. 培养良好的分析思想和与人合作的习惯,体会数学的重要价值.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
1.完全平方公式的推导过程,结构特点,几何解释;
2.完全平方公式的应用.
3. 利用添括号法则灵活应用乘法公式进行运算.
【教学难点】
1. 完全平方公式的特点及整体思想的渗透.
2. 根据式子特点灵活添加括号,使其符合乘法公式特点.
五、课前准备
教师:课件、直尺、矩形、正方形结构图等。
学生:三角尺、练习本、钢笔或圆珠笔、铅笔、直尺。
六、教学过程
(一)导入新课
现有如图所示的三种规格的硬纸片各若干张,请你根据二次三项式a2+2ab+b2,选取相应种类和数量的硬纸片,拼出一个正方形,并探究所拼出的正方形的代数意义.(出示课件2)
(二)探索新知
1.设计问题,探究完全平方公式
教师问1:根据前面所学知识,思考下面这个题目该怎么做?(出示课件4)
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
学生回答:
(1) 直接求:总面积=(a+b)(a+b);
(2) 间接求:总面积=a2+ab+ab+b2
教师问2:你发现了什么?:
学生回答:
(a+b)2=a2+2ab+b2
教师问3:计算下列多项式的积,你能发现什么规律?(出示课件5)
(1) (p+1)2=(p+1)(p+1)=
(2) (m+2)2=(m+2)(m+2)=
(3) (p–1)2=(p–1)(p–1)= .
(4) (m–2)2=(m–2)(m–2)= .
学生计算结果如下:
(1)p2+2p+1;(2)m2+4m+4;(3)p2–2p+1;(4)m2–4m+4。
学生交流并且讨论后回答:两个数和的平方,等于这两个数的平方和加上这两个数乘积的两倍;两个数差的平方,等于这两个数的平方和减去这两个数乘积的两倍.
教师问4:根据你发现的规律,你能写出下列式子的答案吗?
学生回答:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.
教师总结:(出示课件6)
完全平方公式
文字叙述:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
符号叙述:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2.
简记为:
“首平方,尾平方,积的2倍放中央”
教师问5:怎么验证这一规律呢?
学生回答:可以通过计算来验证.(学生小组内独立完成)
教师问6:你能根据下面图形的面积说明完全平方公式吗 (出示课件7)
学生讨论后得出:就是如何验证(a+b)2=a2+2ab+b2
师生共同解答如下:图中可以看出大正方形的边长是a+b,还可以看出大正方形是由两个小正方形和两个矩形组成,所以大正方形的面积等于这四个图形的面积之和.阴影部分的正方形边长是a,所以它的面积是a2.另一个小正方形的边长是b,所以它的面积是b2.另外两个矩形的长都是a,宽都是b,所以每个矩形的面积都是ab;大正方形的边长是a+b,其面积是(a+b)2.于是就可以得出:(a+b)2=a2+2ab+b2.
教师问7:如何验证(a-b)2=a2-2ab+b2?
学生小组讨论后回答:
如图2中,大正方形的边长是a,它的面积是a2;两个矩形是全等图形,长都是a,宽都是b,所以它们的面积都是ab;李淼小正方形的边长是b,其面积就是b2;里面大正方形的边长是(a-b),所以它的面积是(a-b)2.从图中可以看出里面大正方形的面积等于外面大正方形的面积减去两个矩形的面积再加上小正方形的面积,也就是(a-b)2=a2-2ab+b2.
教师展示课件9-10,帮助学生理解公式。
教师问8:(出示课件11)
观察下面两个完全平方式,比一比,回答下列问题:
(a+b)2=a2+2ab+b2.
(a-b)2=a2-2ab+b2
教师问(1) :说一说积的次数和项数.
学生回答:积的次数都是2次,项数都是3项
教师问(2): 两个完全平方式的积有相同的项吗?与a,b有什么关系?
学生回答:两个完全平方式的积有相同的项,是a2和b2.
教师问(3) :两个完全平方式的积中不同的是哪一项?与a, b有什么关系?它的符号与什么有关?
学生回答:两个完全平方式的积中不同的是2ab,是a, b乘积的2倍,它的符号与b前边的符号一致.
总结点拨:(出示课件12)
公式特征:
1. 积为二次三项式;
2. 积中两项为两数的平方和;
3. 另一项是两数积的2倍,且与两数中间的符号相同.
4. 公式中的字母a,b可以表示数、单项式和多项式.
例1:运用完全平方公式计算:(出示课件14)
(1)(4m+n)2;(2) (y-)2
师生共同解答如下:
例2:运用完全平方公式计算:(出示课件16)
(1) 1022;(2) 992.
师生共同解答如下:
解:(1) 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
=(100-1)2
=10000 –200+1
=9801.
总结点拨:当一个数具备与整十、整百……相差一个正整数时求它的平方,我们可以通过变形运用完全平方公式进行运算较简便.
例3:已知x–y=6,xy=–8.(出示课件18)
求:(1) x2+y2的值; (2)(x+y)2的值.
师生共同解答如下:
解:(1)∵x–y=6,xy=–8,
(x–y)2=x2+y2–2xy,
∴x2+y2=(x–y)2+2xy
=36 –16=20;
(2)∵x2+y2=20,xy=–8,
∴(x+y)2=x2+y2+2xy
=20 –16=4.
总结点拨:本题要熟练掌握完全平方公式的变式:
x2+y2=(x–y)2+2xy=(x+y)2–2xy,(x–y)2=(x+y)2–4xy.
2.创设情境,探究添括号法则
教师问9:同学们完成下列运算.
(1)4+(5+2); (2)4-(5+2); (3)a+(b+c); (4)a-(b-c).
学生回答:
(1)4+(5+2)=4+5+2=9+2=11;
(2)4-(5+2)=4-5-2=-3;
(3)a+(b+c)=a+b+c;
(4)a-(b-c)=a-b+c.
教师问10:去括号法则是什么呢?.
学生回答:
去括号时,如果括号前是正号,去掉括号后,括号里的每一项都不改变符号;如果括号前是负号,去掉括号后,括号里的各项都改变符号.
也就是说,遇“加”不变,遇“减”都变.
教师问11:把下面两个等式的左右两边反过来,得到什么?(出示课件20)
a+(b+c)=a+b+c; a-(b+c)=a-b-c.
学生回答:
a + b + c = a + ( b + c) ;
a – b - c = a – ( b + c ) .
教师问12:你能总结出添括号法则吗?
学生小结:添括号其实就是把去括号反过来。
也是:遇“加”不变,遇“减”都变.
总结点拨:(出示课件21)
添括号法则是去括号法则反过来得到的,无论是添括号,还是去括号,运算前后代数式的值都保持不变,所以我们可以用去括号法则验证所添括号后的代数式是否正确.
例4:运用乘法公式计算:(出示课件22)
(1) (x+2y–3)(x–2y+3) ; (2) (a+b+c)2.
师生共同解答如下:
解: (1)原式=[x+(2y–3)][x–(2y–3)]
= x2–(2y–3)2
= x2–(4y2–12y+9)
= x2–4y2+12y–9.
(2)原式= [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
(三)课堂练习(出示课件25-28)
1. 运用乘法公式计算(a–2)2的结果是( )
A.a2–4a+4 B.a2–2a+4
C.a2–4 D.a2–4a–4
2.下列计算结果为2ab–a2–b2的是( )
A.(a–b)2 B.(–a–b)2
C.–(a+b)2 D.–(a–b)2
3.运用完全平方公式计算:
(1) (6a+5b)2=_______________;(2) (4x–3y)2=_______________ ;
(3) (2m–1)2 =_______________;(4)(–2m–1)2 =_______________.
4.由完全平方公式可知:32+2×3×5+52=(3+5)2=64,运用这一方法计算:4.3212+8.642×0.679+0.6792=________.
5. 计算:(1)(3a+b–2)(3a–b+2);(2)(x–y–m+n)(x–y+m–n).
6. 若a+b=5,ab=–6, 求a2+b2,a2–ab+b2.
7. 已知x+y=8,x–y=4,求xy.
参考答案:
1.A
2.D
3.(1) 36a2+60ab+25b2;(2)16x2–24xy+9y2;(3)4m2–4m+1;(4)4m2+4m+1
4.25
5. 解:(1)原式=[3a+(b–2)][3a–(b–2)] =(3a)2–(b–2)2
=9a2–b2+4b–4.
(2)原式=[(x–y)–(m–n)][(x–y)+(m–n)]
=(x–y)2–(m–n)2
=x2–2xy+y2–m2+2mn–n2.
6. 解:a2+b2=(a+b)2–2ab=52–2×(–6)=37;
7. 解:∵x+y=8, ∴(x+y)2=64,即x2+y2+2xy=64①;
∵x–y=4, ∴(x–y)2=16,即x2+y2–2xy=16②;
由①–②得4xy=48,∴xy=12.
(四)课堂小结
今天我们学了哪些内容:
1. 完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
2. 添括号法则:遇“加”不变,遇“减”都变.
(五)课前预习
预习下节课(14.3.1)的相关内容。
知道公因式、提公因式法的定义
七、课后作业
1、教材110页练习1,2和教材111页练习1,2
2、如图,长方形ABCD的周长是20 cm,以AB,AD为边分别向外作正方形ABEF和正方形ADGH,若正方形ABEF和正方形ADGH的面积之和为68 cm2,那么长方形ABCD的面积是( )
A.21 cm2 B.16 cm2 C.24 cm2 D.9 cm2
八、板书设计:
九、教学反思:
1. 本节课充分发挥了学生自主学习、探究的能力.从归纳猜想、随堂练习到公式验证、巩固提高,都渗透着从学生自主探索,再到学生与学生之间的合作交流学习,都突出了学生是探索性学习活动的主体这一理念.此外,还充分挖掘本课时教材中的隐含的各种数学思想,在教学中渗透如数形结合思想、换元思想、化归思想,注重培养学生发现问题、解决问题的能力.
2. 本节课是在学方差公式与完全平方公式之后进行的,本课时中的内容不多,但对知识的要求较高,难点也较多,对学生的要求也较高,所以对课堂教学的组织要求就更高.因此在设计活动时,紧紧围绕着乘法公式的形式展开,并根据活动情况不断地变换问题,以问题为核心调动学生参与活动的兴趣与积极性,在每一个教学环节都对学生提出了不同的要求.
