【核心素养目标】4.6利用相似三角形测高度 教学设计
文档属性
| 名称 | 【核心素养目标】4.6利用相似三角形测高度 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.6利用相似三角形测高度教学设计
课题 4.6利用相似三角形测高度 单元 4 学科 数学 年级 九
教材分析 本节课的内容是《探索三角形相似的条件》之后的复习与应用,它将生活中一些无法直接测量物体高度的实际问题转化为数学问题,利用学生已有的相似三角形的知识采用不同的方法给予解决。通过对此问题的解决方案的探究,巩固相似三角形的判定和定义性质,渗透数形结合和建模的思想,从而提高学生解决实际问题的能力,增强应用意识。
核心素养 通过设计测量旗杆高度的方案,学生学会由实物图形抽象成几何的方法,加强数形结合和建模的思想,提高解决实际问题的能力。
学习 目标 1、通过测量旗杆的高度,综合运用三角形相似的判定定理和相似三角形的定义解决问题,加深对相似三角形的理解和认识。 2、通过设计测量旗杆高度的方案,学会由实物图形抽象成几何的方法,加强数形结合和建模的思想,提高解决实际问题的能力。
重点 理解用不同方法构造相似三角形测高的原理
难点 如何在操作步骤中发掘三角形相似的条件
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 1.问题:相似三角形的判定方法有哪些? 2.胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度,你能根据图示说出他测量金字塔的原理吗? 学生思考,回答问题 通过带学生回顾相似三角形的判定以及金字塔的情景,让学生明白数学源于生活又服务生活.
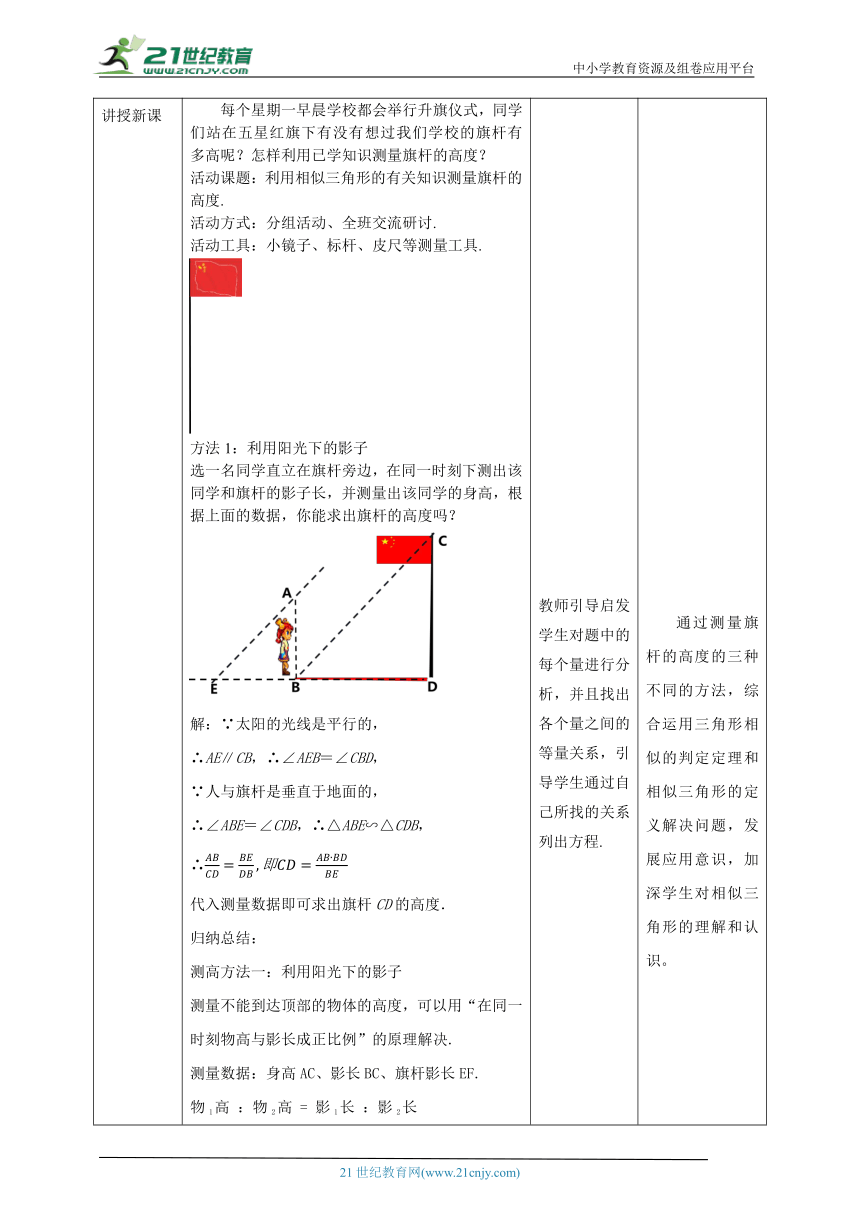
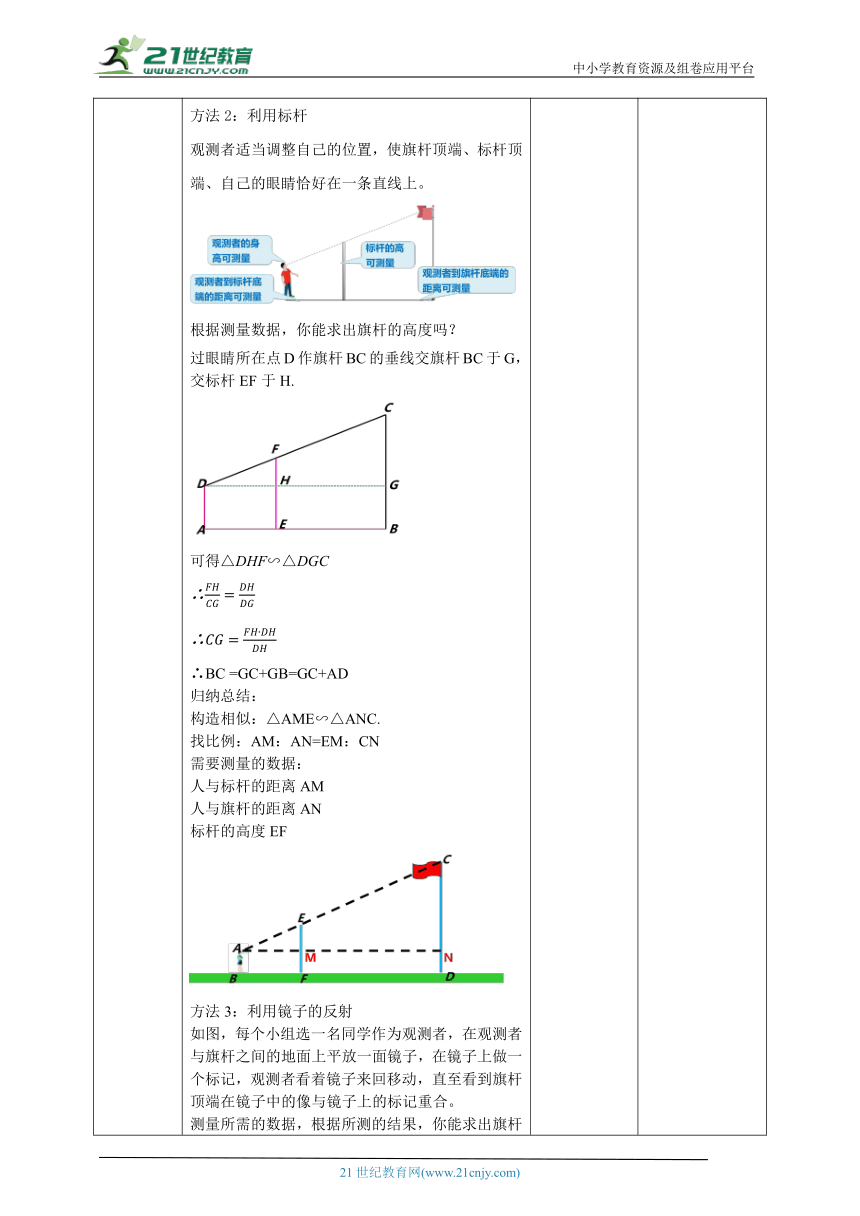
讲授新课 每个星期一早晨学校都会举行升旗仪式,同学们站在五星红旗下有没有想过我们学校的旗杆有多高呢?怎样利用已学知识测量旗杆的高度? 活动课题:利用相似三角形的有关知识测量旗杆的高度. 活动方式:分组活动、全班交流研讨. 活动工具:小镜子、标杆、皮尺等测量工具. 方法1:利用阳光下的影子 选一名同学直立在旗杆旁边,在同一时刻下测出该同学和旗杆的影子长,并测量出该同学的身高,根据上面的数据,你能求出旗杆的高度吗? 解:∵太阳的光线是平行的, ∴AE∥CB,∴∠AEB=∠CBD, ∵人与旗杆是垂直于地面的, ∴∠ABE=∠CDB,∴△ABE∽△CDB, ∴ 代入测量数据即可求出旗杆CD的高度. 归纳总结: 测高方法一:利用阳光下的影子 测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. 测量数据:身高AC、影长BC、旗杆影长EF. 物1高 :物2高 = 影1长 :影2长 方法2:利用标杆 观测者适当调整自己的位置,使旗杆顶端、标杆顶端、自己的眼睛恰好在一条直线上。 根据测量数据,你能求出旗杆的高度吗? 过眼睛所在点D作旗杆BC的垂线交旗杆BC于G,交标杆EF于H. 可得△DHF∽△DGC ∴ ∴ ∴BC =GC+GB=GC+AD 归纳总结: 构造相似:△AME∽△ANC. 找比例:AM:AN=EM:CN 需要测量的数据: 人与标杆的距离AM 人与旗杆的距离AN 标杆的高度EF 方法3:利用镜子的反射 如图,每个小组选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合。 测量所需的数据,根据所测的结果,你能求出旗杆的高度吗?说明你的理由。 解:∵入射角=反射角, ∴∠AEB=∠CED. ∵人、旗杆都垂直于地面, ∴∠B=∠D=90°,∴△AEB∽△CED, ∴ ∴ 因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度. 归纳总结: “利用镜子的反射测量高度”的原理解决. 找相似:△ABE∽△CDE. 找比例:AB:CD=BE:DE 测量数据:人眼睛到地面高度AB、人与镜子间的距离BE、旗杆与镜子间距离DE. 想一想: 上述三种测量方法的基本思路是什么? 综合运用三角形相似的判定和性质解决问题,其方法是: (1)将实际问题转化为相似三角形问题; (2)想方设法找出一对相似三角形; (3)根据相似三角形性质,建立比例式,求出相应的量. 议一议: 上述几种测量方法各有哪些优缺点? (1)测量数据较少,结果较准确;但需要有阳光即影子. (2)不依靠影子,结果准确;但测量数据较多. (3)测量数据较少,不依靠影子;但镜子角度有一点误差,结果就会误差很大. 教师引导启发学生对题中的每个量进行分析,并且找出各个量之间的等量关系,引导学生通过自己所找的关系列出方程. 学生思考回答问题 通过测量旗杆的高度的三种不同的方法,综合运用三角形相似的判定定理和相似三角形的定义解决问题,发展应用意识,加深学生对相似三角形的理解和认识。 通过学生思考,区分三种方法的优缺点,可以让学生更好的选择方法.
课堂练习 1.小明在测量楼高时,测出楼房落在地面上的影长BA为15米,同时在A处竖立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( ) A.10米 B.12米 C.15米 D.22.5米 2.如图,身高为1.6米的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是( ) A.6.4米 B.7.0米 C.8.0米 D.9.0米 3.如图所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24 cm,则点光源S到平面镜的距离SA的长度为 . 4.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DE=8cm,DF=10cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m. 5. 高4m的旗杆在水平地面上的影子长6 m,此时测得附近一个建筑物的影子长24 m,求该建筑物的高度. 自主完成练习,然后集体交流评价. 通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯.
课堂小结 谈一谈这节课有什么收获? 学生总结,分享收获 鼓励学生结合本节课的学习过程,自觉总结,并自觉地应用到现实之中,逐步形成正确的数学观,培养学生的审美意识。
板书 课题:4.6利用相似三角形测高度证明 一、利用阳光下的影子: 二、利用标杆: 三、利用镜子的反射测量高度
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.6利用相似三角形测高度教学设计
课题 4.6利用相似三角形测高度 单元 4 学科 数学 年级 九
教材分析 本节课的内容是《探索三角形相似的条件》之后的复习与应用,它将生活中一些无法直接测量物体高度的实际问题转化为数学问题,利用学生已有的相似三角形的知识采用不同的方法给予解决。通过对此问题的解决方案的探究,巩固相似三角形的判定和定义性质,渗透数形结合和建模的思想,从而提高学生解决实际问题的能力,增强应用意识。
核心素养 通过设计测量旗杆高度的方案,学生学会由实物图形抽象成几何的方法,加强数形结合和建模的思想,提高解决实际问题的能力。
学习 目标 1、通过测量旗杆的高度,综合运用三角形相似的判定定理和相似三角形的定义解决问题,加深对相似三角形的理解和认识。 2、通过设计测量旗杆高度的方案,学会由实物图形抽象成几何的方法,加强数形结合和建模的思想,提高解决实际问题的能力。
重点 理解用不同方法构造相似三角形测高的原理
难点 如何在操作步骤中发掘三角形相似的条件
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 1.问题:相似三角形的判定方法有哪些? 2.胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度,你能根据图示说出他测量金字塔的原理吗? 学生思考,回答问题 通过带学生回顾相似三角形的判定以及金字塔的情景,让学生明白数学源于生活又服务生活.
讲授新课 每个星期一早晨学校都会举行升旗仪式,同学们站在五星红旗下有没有想过我们学校的旗杆有多高呢?怎样利用已学知识测量旗杆的高度? 活动课题:利用相似三角形的有关知识测量旗杆的高度. 活动方式:分组活动、全班交流研讨. 活动工具:小镜子、标杆、皮尺等测量工具. 方法1:利用阳光下的影子 选一名同学直立在旗杆旁边,在同一时刻下测出该同学和旗杆的影子长,并测量出该同学的身高,根据上面的数据,你能求出旗杆的高度吗? 解:∵太阳的光线是平行的, ∴AE∥CB,∴∠AEB=∠CBD, ∵人与旗杆是垂直于地面的, ∴∠ABE=∠CDB,∴△ABE∽△CDB, ∴ 代入测量数据即可求出旗杆CD的高度. 归纳总结: 测高方法一:利用阳光下的影子 测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决. 测量数据:身高AC、影长BC、旗杆影长EF. 物1高 :物2高 = 影1长 :影2长 方法2:利用标杆 观测者适当调整自己的位置,使旗杆顶端、标杆顶端、自己的眼睛恰好在一条直线上。 根据测量数据,你能求出旗杆的高度吗? 过眼睛所在点D作旗杆BC的垂线交旗杆BC于G,交标杆EF于H. 可得△DHF∽△DGC ∴ ∴ ∴BC =GC+GB=GC+AD 归纳总结: 构造相似:△AME∽△ANC. 找比例:AM:AN=EM:CN 需要测量的数据: 人与标杆的距离AM 人与旗杆的距离AN 标杆的高度EF 方法3:利用镜子的反射 如图,每个小组选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合。 测量所需的数据,根据所测的结果,你能求出旗杆的高度吗?说明你的理由。 解:∵入射角=反射角, ∴∠AEB=∠CED. ∵人、旗杆都垂直于地面, ∴∠B=∠D=90°,∴△AEB∽△CED, ∴ ∴ 因此,测量出人与镜子的距离BE,旗杆与镜子的距离DE,再知道人的身高AB,就可以求出旗杆CD的高度. 归纳总结: “利用镜子的反射测量高度”的原理解决. 找相似:△ABE∽△CDE. 找比例:AB:CD=BE:DE 测量数据:人眼睛到地面高度AB、人与镜子间的距离BE、旗杆与镜子间距离DE. 想一想: 上述三种测量方法的基本思路是什么? 综合运用三角形相似的判定和性质解决问题,其方法是: (1)将实际问题转化为相似三角形问题; (2)想方设法找出一对相似三角形; (3)根据相似三角形性质,建立比例式,求出相应的量. 议一议: 上述几种测量方法各有哪些优缺点? (1)测量数据较少,结果较准确;但需要有阳光即影子. (2)不依靠影子,结果准确;但测量数据较多. (3)测量数据较少,不依靠影子;但镜子角度有一点误差,结果就会误差很大. 教师引导启发学生对题中的每个量进行分析,并且找出各个量之间的等量关系,引导学生通过自己所找的关系列出方程. 学生思考回答问题 通过测量旗杆的高度的三种不同的方法,综合运用三角形相似的判定定理和相似三角形的定义解决问题,发展应用意识,加深学生对相似三角形的理解和认识。 通过学生思考,区分三种方法的优缺点,可以让学生更好的选择方法.
课堂练习 1.小明在测量楼高时,测出楼房落在地面上的影长BA为15米,同时在A处竖立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( ) A.10米 B.12米 C.15米 D.22.5米 2.如图,身高为1.6米的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0米,BC=8.0米,则旗杆的高度是( ) A.6.4米 B.7.0米 C.8.0米 D.9.0米 3.如图所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10cm,BC=20cm,PC⊥AC,且PC=24 cm,则点光源S到平面镜的距离SA的长度为 . 4.如图,小颖同学用自制的直角三角形纸板DEF测量树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条边DE=8cm,DF=10cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=________m. 5. 高4m的旗杆在水平地面上的影子长6 m,此时测得附近一个建筑物的影子长24 m,求该建筑物的高度. 自主完成练习,然后集体交流评价. 通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯.
课堂小结 谈一谈这节课有什么收获? 学生总结,分享收获 鼓励学生结合本节课的学习过程,自觉总结,并自觉地应用到现实之中,逐步形成正确的数学观,培养学生的审美意识。
板书 课题:4.6利用相似三角形测高度证明 一、利用阳光下的影子: 二、利用标杆: 三、利用镜子的反射测量高度
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
