人教版数学七年级上册 2.3整式的加减小结课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级上册 2.3整式的加减小结课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 408.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 11:03:00 | ||
图片预览





文档简介
(共19张PPT)
2.3 整式的加减小结
七年级上册 RJ
初中数学
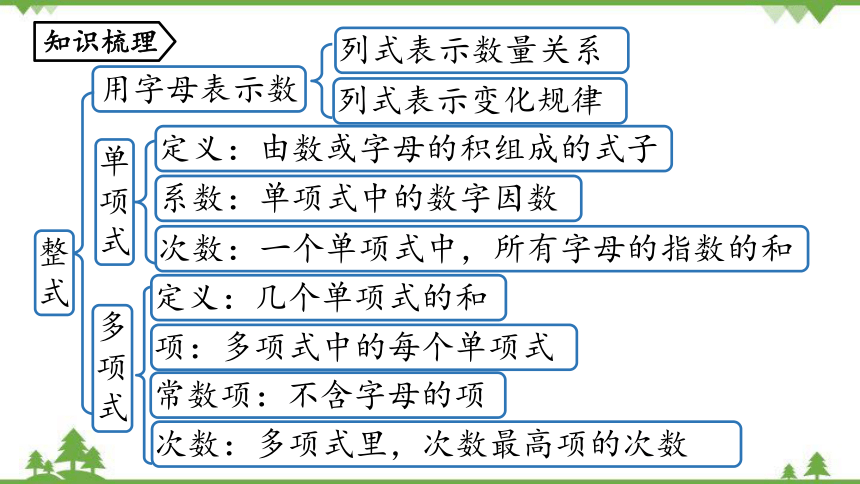
列式表示数量关系
列式表示变化规律
用字母表示数
定义:由数或字母的积组成的式子
系数:单项式中的数字因数
次数:一个单项式中,所有字母的指数的和
单项式
定义:几个单项式的和
项:多项式中的每个单项式
常数项:不含字母的项
多项式
次数:多项式里,次数最高项的次数
知识梳理
整式
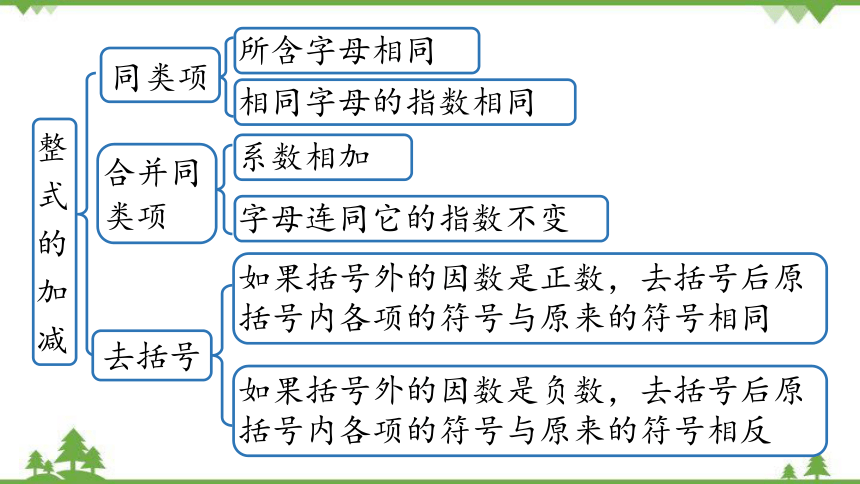
整式的加减
所含字母相同
相同字母的指数相同
同类项
系数相加
字母连同它的指数不变
合并同类项
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
去括号
2.单项式的系数:单项式中的数字因数叫做这个单项式的系数.
一、整式的有关概念
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1.单项式:由数或字母的积组成的式子叫做单项式,单独的一个数或一个字母也是单项式.
4.多项式:几个单项式的和叫做多项式.
6.整式:单项式与多项式统称整式.
5.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
二、同类项、合并同类项
1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.
注意:(1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项;(2)只有同类项才能合并,如x2+x3不能合并.
三、整式的加减
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
1.由于受H7N9禽流感的影响,我市某城区前年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克.设3月份鸡的价格为m元/千克,则( )
A.m=24(1- a% - b%) B.m=24(1- a%)b%
C.m=24 - a% - b% D.m=24(1- a%)(1- b%)
D
重难剖析
解:因为2月份鸡的价格比1月份下降a%,1月份鸡的价格为24元/千克,
所以2月份鸡的价格为24(1- a%)元/千克.
因为3月份鸡的价格比2月份下降b%,
所以3月份鸡的价格为24(1- a%)(1- b%)元/千克.
A
单项式不含加减运算
3.若3xm+5y2与x3yn的和是单项式,求mn的值.
解:由题意得m+5=3,n=2,
即 m=-2,n=2,
所以mn=(-2)2=4.
两个单项式的和仍是单项式,说明这两个单项式是同类项.
4.已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1) A+B;(2) 2B-2A.
解:(1) A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2) 2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
5.若A是一个三次多项式,B是一个四次多项式,则A+B一定是( )
A.三次多项式 B.四次多项式或单项式
C.七次多项式 D.四次七项式
B
解析:A+B的最高次项一定是四次项,至于是否含有其他低次项不得而知,
所以A+B只可能是四次多项式或单项式.
6.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6……按照上述规律,第2 021个单项式是( )
A.2 020x2 021 B.4 039x2 021
C.4 041x2 021 D.4 041x2 020
解析:观察单项式得第n个单项式为(2n-1)xn,
所以第2 021个单项式是(2×2 021-1)x2 021=4041x2 021.
C
3
能力提升
单项式的系数:单项式中的数字因数.
单项式的次数:所有字母的指数的和.
2.(1) 若5x2y与xmyn是同类项,则m=( ),n=( ).
2
1
1
1
(2) 若单项式a2b与3am+nbn能合并,则m=( ),n=( ).
两个单项式能合并,说明这两个单项式是同类项.
3.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
注意:去括号法则的正确使用.
4.若A是一个四次多项式,B是一个二次多项式,则A-B( )
A.可能是六次多项式 B.可能是二次多项式
C.一定是四次多项式或单项式 D.可能是0
C
解析:A-B的最高次项一定是四次项,至于是否含有其他低次项不得而知,
所以A-B只可能是四次多项式或单项式.
根据图中棋子的排列规律解决下列问题:
(1) 第4个图中有 枚棋子,第5个图中有 枚棋子;
(2) 猜想第n个图中棋子的数量是 (用含n的式子表示).
5.如图是用棋子摆成的图案:
22
32
2+n+n2
2.3 整式的加减小结
七年级上册 RJ
初中数学
列式表示数量关系
列式表示变化规律
用字母表示数
定义:由数或字母的积组成的式子
系数:单项式中的数字因数
次数:一个单项式中,所有字母的指数的和
单项式
定义:几个单项式的和
项:多项式中的每个单项式
常数项:不含字母的项
多项式
次数:多项式里,次数最高项的次数
知识梳理
整式
整式的加减
所含字母相同
相同字母的指数相同
同类项
系数相加
字母连同它的指数不变
合并同类项
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反
去括号
2.单项式的系数:单项式中的数字因数叫做这个单项式的系数.
一、整式的有关概念
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
1.单项式:由数或字母的积组成的式子叫做单项式,单独的一个数或一个字母也是单项式.
4.多项式:几个单项式的和叫做多项式.
6.整式:单项式与多项式统称整式.
5.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.
二、同类项、合并同类项
1.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.
注意:(1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项;(2)只有同类项才能合并,如x2+x3不能合并.
三、整式的加减
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
1.由于受H7N9禽流感的影响,我市某城区前年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克.设3月份鸡的价格为m元/千克,则( )
A.m=24(1- a% - b%) B.m=24(1- a%)b%
C.m=24 - a% - b% D.m=24(1- a%)(1- b%)
D
重难剖析
解:因为2月份鸡的价格比1月份下降a%,1月份鸡的价格为24元/千克,
所以2月份鸡的价格为24(1- a%)元/千克.
因为3月份鸡的价格比2月份下降b%,
所以3月份鸡的价格为24(1- a%)(1- b%)元/千克.
A
单项式不含加减运算
3.若3xm+5y2与x3yn的和是单项式,求mn的值.
解:由题意得m+5=3,n=2,
即 m=-2,n=2,
所以mn=(-2)2=4.
两个单项式的和仍是单项式,说明这两个单项式是同类项.
4.已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1) A+B;(2) 2B-2A.
解:(1) A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2) 2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
5.若A是一个三次多项式,B是一个四次多项式,则A+B一定是( )
A.三次多项式 B.四次多项式或单项式
C.七次多项式 D.四次七项式
B
解析:A+B的最高次项一定是四次项,至于是否含有其他低次项不得而知,
所以A+B只可能是四次多项式或单项式.
6.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6……按照上述规律,第2 021个单项式是( )
A.2 020x2 021 B.4 039x2 021
C.4 041x2 021 D.4 041x2 020
解析:观察单项式得第n个单项式为(2n-1)xn,
所以第2 021个单项式是(2×2 021-1)x2 021=4041x2 021.
C
3
能力提升
单项式的系数:单项式中的数字因数.
单项式的次数:所有字母的指数的和.
2.(1) 若5x2y与xmyn是同类项,则m=( ),n=( ).
2
1
1
1
(2) 若单项式a2b与3am+nbn能合并,则m=( ),n=( ).
两个单项式能合并,说明这两个单项式是同类项.
3.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
注意:去括号法则的正确使用.
4.若A是一个四次多项式,B是一个二次多项式,则A-B( )
A.可能是六次多项式 B.可能是二次多项式
C.一定是四次多项式或单项式 D.可能是0
C
解析:A-B的最高次项一定是四次项,至于是否含有其他低次项不得而知,
所以A-B只可能是四次多项式或单项式.
根据图中棋子的排列规律解决下列问题:
(1) 第4个图中有 枚棋子,第5个图中有 枚棋子;
(2) 猜想第n个图中棋子的数量是 (用含n的式子表示).
5.如图是用棋子摆成的图案:
22
32
2+n+n2
