平行四边形判定的应用(三角形中位线定理)[下学期]
文档属性
| 名称 | 平行四边形判定的应用(三角形中位线定理)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 262.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-17 00:00:00 | ||
图片预览

文档简介
课件11张PPT。平行四边形判定的应用
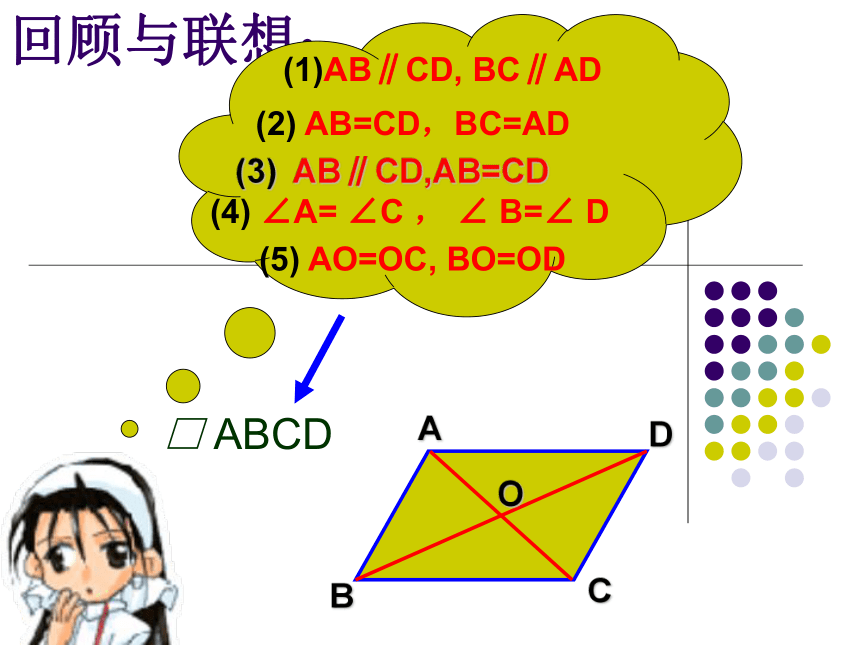
(中位线定理)19.1.2回顾与联想:□ ABCD(1)AB∥CD, BC∥AD(2) AB=CD,BC=AD (4) ∠A= ∠C , ∠ B=∠ D(5) AO=OC, BO=OD(3) AB∥CD,AB=CDABCDOABB′A′CC′在学习平移时,我们通过探究发现,平移时对应
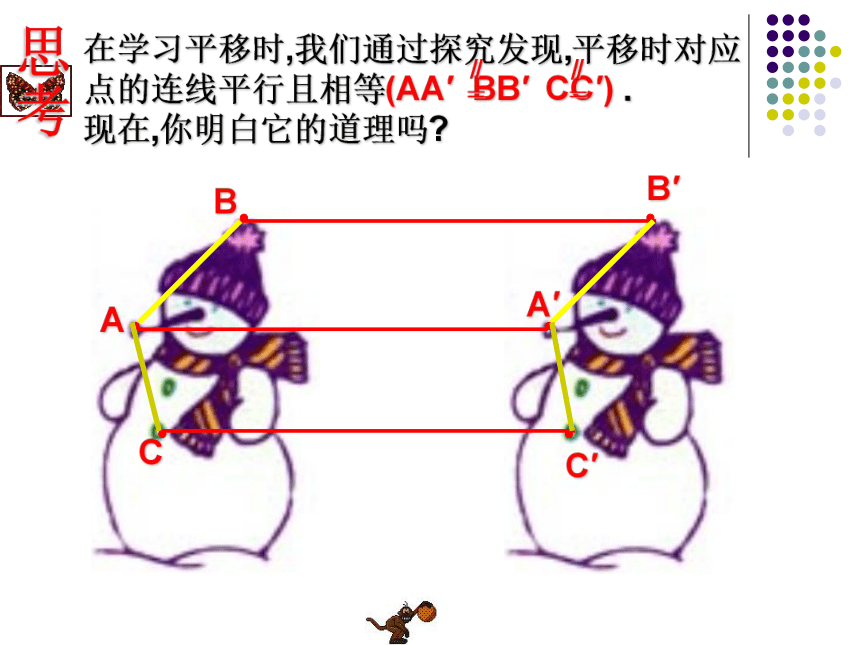
点的连线平行且相等(AA′ BB′ CC′) .
现在,你明白它的道理吗?∥
=∥
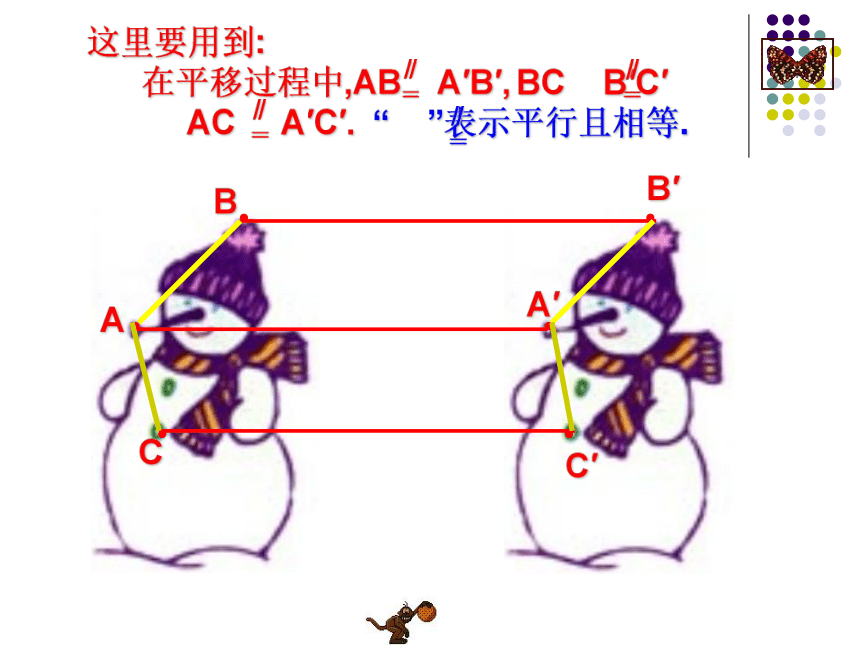
=思考ABB′A′CC′这里要用到:
在平移过程中,AB A′B′, BC B′C′
AC A′C′. “ ”表示平行且相等.∥
=∥
=∥
=∥
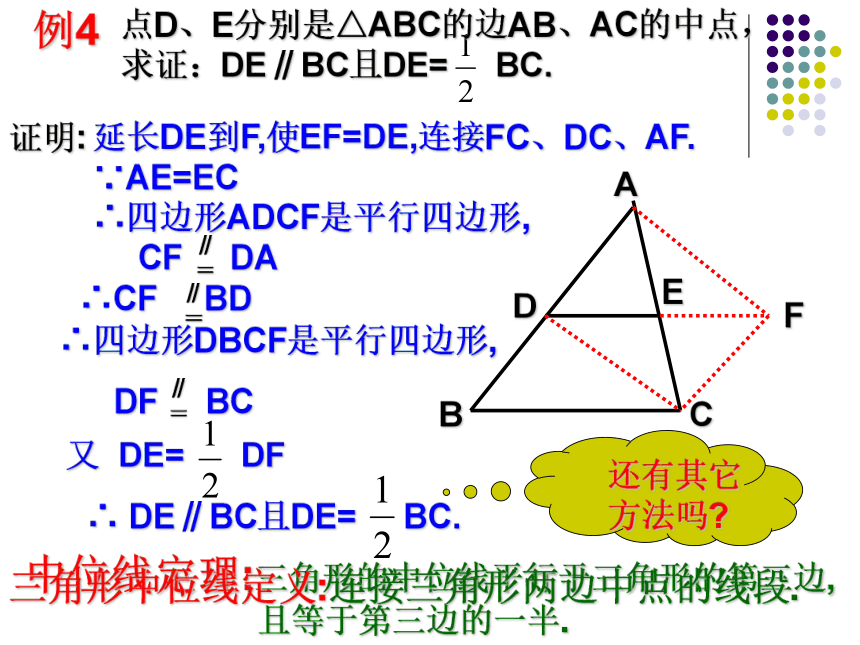
=例4点D、E分别是△ABC的边AB、AC的中点,
求证:DE∥BC且DE= BC.AEDBCF证明: 延长DE到F,使EF=DE,连接FC、DC、AF.
∵AE=EC
∴四边形ADCF是平行四边形,
CF DA∥
=∴CF BD∥
=∴四边形DBCF是平行四边形,DF BC∥
=又 DE= DF∴ DE∥BC且DE= BC.中位线定理:三角形的中位线平行于三角形的第三边,
且等于第三边的一半.还有其它
方法吗?三角形中位线定义:连接三角形两边中点的线段.想一想(1)一个三角形有_____条中位线.
(2)一个三角形有_____条线.
(3)中位线和中线有什么区别?
33练习P99.1.3.做一做1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
2. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.AEDCB(1)AEDBC(2)能力提升已知:E为平行四边形ABCD中DC边的延长线
上一点,且CE=DC,连结AE,分别交BC、BD于
点F、G,连接AC交BD于O,连结OF.
求证: AB= 2 OFADBCEGFO提示:证明△ABF≌ △ECF,
得BF=CF,再证OF是
△ABC的中位线.驶向胜利的彼岸祝你成功!这堂我们学到了什么?
(中位线定理)19.1.2回顾与联想:□ ABCD(1)AB∥CD, BC∥AD(2) AB=CD,BC=AD (4) ∠A= ∠C , ∠ B=∠ D(5) AO=OC, BO=OD(3) AB∥CD,AB=CDABCDOABB′A′CC′在学习平移时,我们通过探究发现,平移时对应
点的连线平行且相等(AA′ BB′ CC′) .
现在,你明白它的道理吗?∥
=∥
=思考ABB′A′CC′这里要用到:
在平移过程中,AB A′B′, BC B′C′
AC A′C′. “ ”表示平行且相等.∥
=∥
=∥
=∥
=例4点D、E分别是△ABC的边AB、AC的中点,
求证:DE∥BC且DE= BC.AEDBCF证明: 延长DE到F,使EF=DE,连接FC、DC、AF.
∵AE=EC
∴四边形ADCF是平行四边形,
CF DA∥
=∴CF BD∥
=∴四边形DBCF是平行四边形,DF BC∥
=又 DE= DF∴ DE∥BC且DE= BC.中位线定理:三角形的中位线平行于三角形的第三边,
且等于第三边的一半.还有其它
方法吗?三角形中位线定义:连接三角形两边中点的线段.想一想(1)一个三角形有_____条中位线.
(2)一个三角形有_____条线.
(3)中位线和中线有什么区别?
33练习P99.1.3.做一做1.△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
2. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.AEDCB(1)AEDBC(2)能力提升已知:E为平行四边形ABCD中DC边的延长线
上一点,且CE=DC,连结AE,分别交BC、BD于
点F、G,连接AC交BD于O,连结OF.
求证: AB= 2 OFADBCEGFO提示:证明△ABF≌ △ECF,
得BF=CF,再证OF是
△ABC的中位线.驶向胜利的彼岸祝你成功!这堂我们学到了什么?
