4.1数列的概念 人教A版(2019)选择性必修第二册高中数学精品课件(共28张PPT)
文档属性
| 名称 | 4.1数列的概念 人教A版(2019)选择性必修第二册高中数学精品课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 488.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 14:09:52 | ||
图片预览







文档简介
(共28张PPT)
4.1数列的概念
选择性必修二第四章
知识梳理
一、
数列的有关概念
1
.
定义
:按照
________
的顺序排列的一列数.
2
.
项:
数列中的
________
叫做这个数列的项;排在
________
的数
称为这个数列的第
1
项
(
也叫首项
)
.
3
.
一般形式:
a
1
,
a
2
,
a
3
,
…
,
a
n
,
…
,简记为
________
.
知识梳理
知识梳理
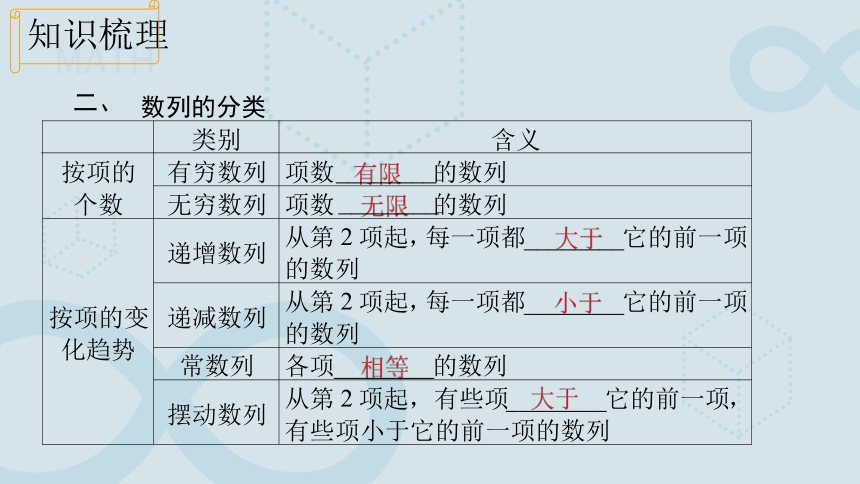
二、
数列的分类
类别
含义
按项的
个数
有穷数列
项数
________
的数列
无穷数列
项数
________
的数列
按项的变
化趋势
递增数列
从第
2
项起
,
每一项都
________
它的前一项
的数列
递减数列
从第
2
项起
,
每一项都
________
它的前一项
的数列
常数列
各项
________
的数列
摆动数列
从第
2
项起,有些项
________
它的前一项
,
有些项小于它的前一项的数列
知识梳理
三、
数列的通项公式
如果数列
{
a
n
}
的
第
n
项
a
n
与
________
之间的关系可以用一个式
子来表示,那么这个公式叫做这个数列的通项公式.
知识梳理
四、
数列与函数的关系
从函数的观点看,数列可以看作是特殊的函数,关系如下表:
定义域
________(
或它的有限子集
{1,2,3
,
…
,
n
})
解析式
数列的通项公式
值域
自变量
___________________________
时对应的一列函
数值构成
表示方法
(1)
通项公式
(
解析法
)
;
(2)________
;
(3)________
知识梳理
五、
数列的递推公式
如果一个数列的
________
两项或多项之间的关系可以用一个
式子来表示,那么这个式子叫做这个数列的递推公式.
知识梳理
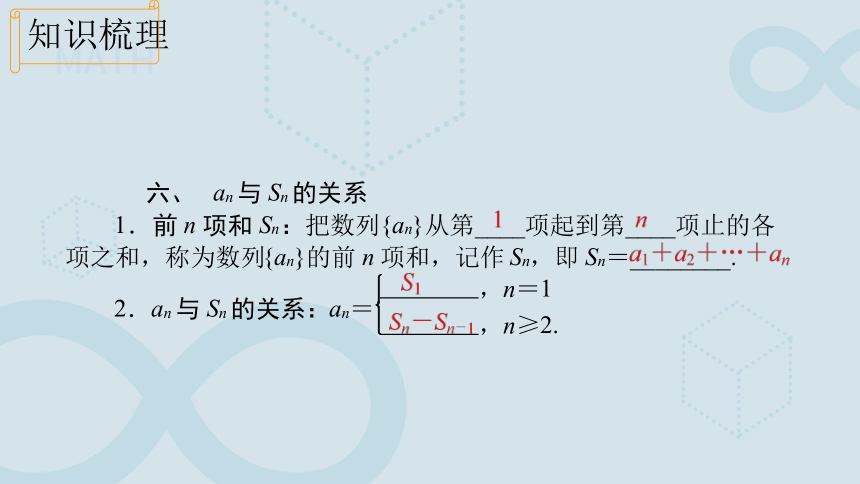
六、
a
n
与
S
n
的关系
1
.
前
n
项和
S
n
:
把数列
{
a
n
}
从第
____
项起到第
____
项止的各
项之和,称为数列
{
a
n
}
的前
n
项和,记作
S
n
,即
S
n
=
________.
2
.
a
n
与
S
n
的关系:
a
n
=
,
n
=
1
,
n
≥
2.
例题解析
判断正误
(
正确的画
“√”
,错误的画
“×”
)
(1){0,1,2,3,4}
是有穷数列.
(
)
(2)
数列
1,2,3,4
和数列
1,2,4,3
是同一数列.
(
)
(3)
所有自然数能构成数列.
(
)
(4)
数列
1,3,5,7
,
…
,
2
n
+
1
,
…
的通项公式是
a
n
=
2
n
+
1.(
)
例题解析
(5)
根据通项公式可以求出数列的任意一项.
(
)
(6)
有些数列可能不存在最大项.
(
)
(7)
递推公式是表示数列的一种方法.
(
)
(8)
所有的数列都有递推公式.
(
)
例题解析
例1
已知下列数列:
①
1,2,2
2,
2
3
,
…
,
2
60
;
②
1,0.5,0.5
2,
0.5
3
,
…
;
③
-
2,2
,-
2,2
,
…
;
④
3,3,3,3
,
…
;
⑤
0
,
1
2
,
2
3
,
3
4
,
…
,
n
-
1
n
,
…
;
⑥
1,0
,-
1
,
…
,
sin
n
2
,
…
.
其中有穷数列是
________
;无穷数列是
________
;
递增数列是
________
;递减数列是
________
;
摆动数列是
________
;常数列是
________
.
(
填序号
)
例题解析
例题解析
A
例题解析
例题解析
例题解析
例题解析
例题解析
B
例题解析
例题解析
例7
已知数列
{
a
n
}
的通项公式为
a
n
=
n
2
-
7
n
-
8.
(1)
数列中有多少项为负数?
(2)
数列
{
a
n
}
是否有最小项?若有,求出其最小项.
例题解析
例题解析
例题解析
例
8
已知数列
{
a
n
}
中,
a
1
=
1
,
a
n
+
1
=
a
n
+
n
+
1
,则
a
n
=
________.
例题解析
变式探究
若将
“
a
n
+
1
=
a
n
+
n
+
1
”
改为
“
a
n
+
1
=
n
n
+
1
a
n
”
,
则
a
n
=
________.
例题解析
例题解析
例10
已知数列
{
a
n
}
的前
n
项和满足
S
n
=
2
n
+
1
-
1
,求数列
{
a
n
}
的通项
公式.
课堂小结
1.数列的概念及分类;
2.由数列的前n项和求通项公式;
3.由数列的递推关系求通项公式;
4. 数列的函数特性。
感谢您的观看
4.1数列的概念
选择性必修二第四章
知识梳理
一、
数列的有关概念
1
.
定义
:按照
________
的顺序排列的一列数.
2
.
项:
数列中的
________
叫做这个数列的项;排在
________
的数
称为这个数列的第
1
项
(
也叫首项
)
.
3
.
一般形式:
a
1
,
a
2
,
a
3
,
…
,
a
n
,
…
,简记为
________
.
知识梳理
知识梳理
二、
数列的分类
类别
含义
按项的
个数
有穷数列
项数
________
的数列
无穷数列
项数
________
的数列
按项的变
化趋势
递增数列
从第
2
项起
,
每一项都
________
它的前一项
的数列
递减数列
从第
2
项起
,
每一项都
________
它的前一项
的数列
常数列
各项
________
的数列
摆动数列
从第
2
项起,有些项
________
它的前一项
,
有些项小于它的前一项的数列
知识梳理
三、
数列的通项公式
如果数列
{
a
n
}
的
第
n
项
a
n
与
________
之间的关系可以用一个式
子来表示,那么这个公式叫做这个数列的通项公式.
知识梳理
四、
数列与函数的关系
从函数的观点看,数列可以看作是特殊的函数,关系如下表:
定义域
________(
或它的有限子集
{1,2,3
,
…
,
n
})
解析式
数列的通项公式
值域
自变量
___________________________
时对应的一列函
数值构成
表示方法
(1)
通项公式
(
解析法
)
;
(2)________
;
(3)________
知识梳理
五、
数列的递推公式
如果一个数列的
________
两项或多项之间的关系可以用一个
式子来表示,那么这个式子叫做这个数列的递推公式.
知识梳理
六、
a
n
与
S
n
的关系
1
.
前
n
项和
S
n
:
把数列
{
a
n
}
从第
____
项起到第
____
项止的各
项之和,称为数列
{
a
n
}
的前
n
项和,记作
S
n
,即
S
n
=
________.
2
.
a
n
与
S
n
的关系:
a
n
=
,
n
=
1
,
n
≥
2.
例题解析
判断正误
(
正确的画
“√”
,错误的画
“×”
)
(1){0,1,2,3,4}
是有穷数列.
(
)
(2)
数列
1,2,3,4
和数列
1,2,4,3
是同一数列.
(
)
(3)
所有自然数能构成数列.
(
)
(4)
数列
1,3,5,7
,
…
,
2
n
+
1
,
…
的通项公式是
a
n
=
2
n
+
1.(
)
例题解析
(5)
根据通项公式可以求出数列的任意一项.
(
)
(6)
有些数列可能不存在最大项.
(
)
(7)
递推公式是表示数列的一种方法.
(
)
(8)
所有的数列都有递推公式.
(
)
例题解析
例1
已知下列数列:
①
1,2,2
2,
2
3
,
…
,
2
60
;
②
1,0.5,0.5
2,
0.5
3
,
…
;
③
-
2,2
,-
2,2
,
…
;
④
3,3,3,3
,
…
;
⑤
0
,
1
2
,
2
3
,
3
4
,
…
,
n
-
1
n
,
…
;
⑥
1,0
,-
1
,
…
,
sin
n
2
,
…
.
其中有穷数列是
________
;无穷数列是
________
;
递增数列是
________
;递减数列是
________
;
摆动数列是
________
;常数列是
________
.
(
填序号
)
例题解析
例题解析
A
例题解析
例题解析
例题解析
例题解析
例题解析
B
例题解析
例题解析
例7
已知数列
{
a
n
}
的通项公式为
a
n
=
n
2
-
7
n
-
8.
(1)
数列中有多少项为负数?
(2)
数列
{
a
n
}
是否有最小项?若有,求出其最小项.
例题解析
例题解析
例题解析
例
8
已知数列
{
a
n
}
中,
a
1
=
1
,
a
n
+
1
=
a
n
+
n
+
1
,则
a
n
=
________.
例题解析
变式探究
若将
“
a
n
+
1
=
a
n
+
n
+
1
”
改为
“
a
n
+
1
=
n
n
+
1
a
n
”
,
则
a
n
=
________.
例题解析
例题解析
例10
已知数列
{
a
n
}
的前
n
项和满足
S
n
=
2
n
+
1
-
1
,求数列
{
a
n
}
的通项
公式.
课堂小结
1.数列的概念及分类;
2.由数列的前n项和求通项公式;
3.由数列的递推关系求通项公式;
4. 数列的函数特性。
感谢您的观看
