高中数学必修第一册人教A版(2019)3.1.1《函数的概念》教学设计(表格式)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)3.1.1《函数的概念》教学设计(表格式) | 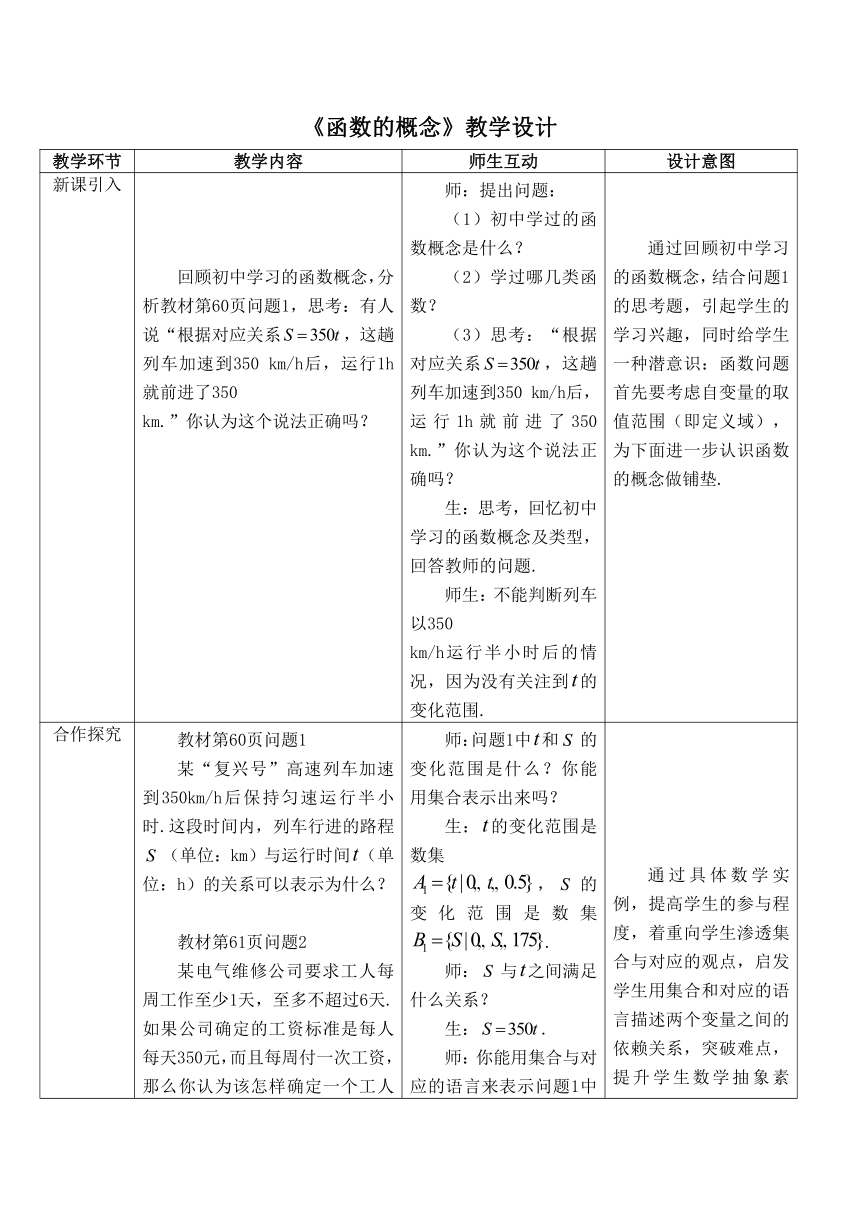 | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 14:42:44 | ||
图片预览



文档简介
《函数的概念》教学设计
教学环节 教学内容 师生互动 设计意图
新课引入 回顾初中学习的函数概念,分析教材第60页问题1,思考:有人说“根据对应关系,这趟列车加速到350 km/h后,运行1h就前进了350 km.”你认为这个说法正确吗? 师:提出问题: (1)初中学过的函数概念是什么? (2)学过哪几类函数? (3)思考:“根据对应关系,这趟列车加速到350 km/h后,运行1h就前进了350 km.”你认为这个说法正确吗? 生:思考,回忆初中学习的函数概念及类型,回答教师的问题. 师生:不能判断列车以350 km/h运行半小时后的情况,因为没有关注到的变化范围. 通过回顾初中学习的函数概念,结合问题1的思考题,引起学生的学习兴趣,同时给学生一种潜意识:函数问题首先要考虑自变量的取值范围(即定义域),为下面进一步认识函数的概念做铺垫.
合作探究 教材第60页问题1 某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.这段时间内,列车行进的路程(单位:km)与运行时间(单位:h)的关系可以表示为什么? 教材第61页问题2 某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么你认为该怎样确定一个工人每周的工资?一个工人的工资(单位:元)是他工作天数的函数吗? 教材第61~62页问题3和问题4. 师:问题1中和的变化范围是什么?你能用集合表示出来吗? 生:的变化范围是数集 ,的变化范围是数集. 师:与之间满足什么关系? 生:. 师:你能用集合与对应的语言来表示问题1中与的对应关系吗? 生:思考、尝试回答. 师生:列车行进的路程与运行时间的对应关系是:①. 其中,的变化范围是数集,的变化范围是数集.对于数集中的任意时刻,按照对应关系①,在数集中都有唯一确定的路程和它对应. 师:分析问题2,引导学生用集合和对应的语言来描述和之间的依赖关系. 生:工资与一周工作天数的对应关系是:.② 其中,的变化范围是数集 ,的变化范围是数集.对于数集中的任一个工作天数,按照对应关系②,在数集中都有唯一确定的工资和它对应. 师:问题1和问题2中的函数有什么异同点? 生:相同的对应关系,但两个变量的范围不一样. 师:你认为它们是同一个函数吗?为什么? 生:不是,因为相应的变量的范围不一样. 师:布置任务:仿照问题1、2,描述问题3、4中两变量间的关系. 生:学生探讨交流,教师巡查、指导. 师:提出问题:通过对4个问题的分析,你能说出它们有什么不同点与共同点吗? 师生:学生认真思考并口答教师提出的问题,在教师的启发、点拨下,学生一般能归纳出以下一些特点: 不同点:问题1.2是用解析式刻画两变量之间的对应关系,问题3是用图象刻画变量之间的对应关系,问题4是用表格刻画变量之间的对应关系. 共同点:①都有两个非空的实数集:②两个实数集之间都有一种确定的对应关系. 教师板书学生提出的这两条共同点,指出解析式、图象、表格都是一种对应关系. 通过具体数学实例,提高学生的参与程度,着重向学生渗透集合与对应的观点,启发学生用集合和对应的语言描述两个变量之间的依赖关系,突破难点,提升学生数学抽象素养.
概念形成 函数的概念: 设,是非空的实数集,如果对于集合中的任意一个数,按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作 ,. 其中,叫做自变量,的取值范围叫做函数的定义域;与的值相对应的值叫做函数值,函数值的集合叫做函数的值域.显然值域是集合的子集. 师:通过对前面4个问题的分析,鼓励学生自己概括出函数的定义. 生:认真体会4个问题的共同点,然后归纳概括出函数的定义并在全班进行交流. 师:(1)板书函数的定义; (2)强调:①对的理解:作为一个整体,它是一种符号,它可以是解析式(如问题1、2),也可以是图象(如问题3),也可以是表格(如问题4).②定义中,是非空的实数集.③对于的每一个值,按照某种确定的对应关系,都有唯一的值和它对应. 利用前面的分析,进行必要的抽象概括,得到函数的定义,培养学生的归纳、概括能力,提升数学抽象素养.同时剖析概念,使学生抓住概念本质,便于理解记忆.
应用举例 1.一次函数的定义域为,值域也为,对应关系把中的任意一个数,对应到中唯一确定的数. 2.二次函数的定义域为,值域是.当时,;当时, .对应关系把中的任意一个数,对应到中唯一确定的数. 3.反比例函数的定义域为,值域为,对应关系把中的任意一个数,对应到中唯一确定的数. 4.例 函数的解析式是舍弃问题的实际背景而抽象出来的,它反映了两个量之间的对应关系,可以广泛地用于刻画一类事物中的变量关系和规律. 试构造一个问题情境,使其中的变量关系可以用解析式来描述. 解:把看成二次函数,那么它的定义域是,值域是.对应关系把中的任意一个数,对应到中唯一确定的数. 师:想一想,初中我们学过了哪些函数? 生:一次函数、二次函数和反比例函数. 师:你能说一说,这三个函数的定义域、值域和对应关系分别是什么吗? 生:思考,回答,其他同学补充. 师:试构造一个问题情境,使其中的变量关系可以用解析式来描述.如果再对的取值范围作出限制,比如呢? 生:尝试构建一些问题情境,然后相互交流、讨论. 师:针对学生的回答进行点评. 引导学生用函数的定义去理解学过的一次函数、二次函数和反比例函数,比较描述性定义与对应语言刻画的定义,加深对函数概念的理解. 引导学生探讨从具体问题情境中抽象出数学模型,以及通过函数解析式去构建问题情境,加深对函数概念的理解.提升学生数学抽象及数学建模素养.
归纳小结 1.函数的概念. 2.三要素. 学生思考、回答,其他同学补充,教师记录、点评.
布置作业 1.教材第63页练习:第1题. 2.教材第64页练习:第4题.
板书设计
第1课时 函数的概念 1.函数的概念 2.函数三要素 定义域 对应关系 值域 问题1 问题2 问题3 问题4 例 小结 1.函数的概念 2.三要素 作业
教学研讨
教材通过集合语言和对应关系刻画函数概念,并建立完整的函数概念,为什么要强调函数是非零实数集合之间的对应关系呢?这个问题有没有必要跟学生解释清楚呢?如果有必要,那什么时候解析比较恰当呢?这些都是值得课后继续探讨的问题.
教学环节 教学内容 师生互动 设计意图
新课引入 回顾初中学习的函数概念,分析教材第60页问题1,思考:有人说“根据对应关系,这趟列车加速到350 km/h后,运行1h就前进了350 km.”你认为这个说法正确吗? 师:提出问题: (1)初中学过的函数概念是什么? (2)学过哪几类函数? (3)思考:“根据对应关系,这趟列车加速到350 km/h后,运行1h就前进了350 km.”你认为这个说法正确吗? 生:思考,回忆初中学习的函数概念及类型,回答教师的问题. 师生:不能判断列车以350 km/h运行半小时后的情况,因为没有关注到的变化范围. 通过回顾初中学习的函数概念,结合问题1的思考题,引起学生的学习兴趣,同时给学生一种潜意识:函数问题首先要考虑自变量的取值范围(即定义域),为下面进一步认识函数的概念做铺垫.
合作探究 教材第60页问题1 某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.这段时间内,列车行进的路程(单位:km)与运行时间(单位:h)的关系可以表示为什么? 教材第61页问题2 某电气维修公司要求工人每周工作至少1天,至多不超过6天.如果公司确定的工资标准是每人每天350元,而且每周付一次工资,那么你认为该怎样确定一个工人每周的工资?一个工人的工资(单位:元)是他工作天数的函数吗? 教材第61~62页问题3和问题4. 师:问题1中和的变化范围是什么?你能用集合表示出来吗? 生:的变化范围是数集 ,的变化范围是数集. 师:与之间满足什么关系? 生:. 师:你能用集合与对应的语言来表示问题1中与的对应关系吗? 生:思考、尝试回答. 师生:列车行进的路程与运行时间的对应关系是:①. 其中,的变化范围是数集,的变化范围是数集.对于数集中的任意时刻,按照对应关系①,在数集中都有唯一确定的路程和它对应. 师:分析问题2,引导学生用集合和对应的语言来描述和之间的依赖关系. 生:工资与一周工作天数的对应关系是:.② 其中,的变化范围是数集 ,的变化范围是数集.对于数集中的任一个工作天数,按照对应关系②,在数集中都有唯一确定的工资和它对应. 师:问题1和问题2中的函数有什么异同点? 生:相同的对应关系,但两个变量的范围不一样. 师:你认为它们是同一个函数吗?为什么? 生:不是,因为相应的变量的范围不一样. 师:布置任务:仿照问题1、2,描述问题3、4中两变量间的关系. 生:学生探讨交流,教师巡查、指导. 师:提出问题:通过对4个问题的分析,你能说出它们有什么不同点与共同点吗? 师生:学生认真思考并口答教师提出的问题,在教师的启发、点拨下,学生一般能归纳出以下一些特点: 不同点:问题1.2是用解析式刻画两变量之间的对应关系,问题3是用图象刻画变量之间的对应关系,问题4是用表格刻画变量之间的对应关系. 共同点:①都有两个非空的实数集:②两个实数集之间都有一种确定的对应关系. 教师板书学生提出的这两条共同点,指出解析式、图象、表格都是一种对应关系. 通过具体数学实例,提高学生的参与程度,着重向学生渗透集合与对应的观点,启发学生用集合和对应的语言描述两个变量之间的依赖关系,突破难点,提升学生数学抽象素养.
概念形成 函数的概念: 设,是非空的实数集,如果对于集合中的任意一个数,按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作 ,. 其中,叫做自变量,的取值范围叫做函数的定义域;与的值相对应的值叫做函数值,函数值的集合叫做函数的值域.显然值域是集合的子集. 师:通过对前面4个问题的分析,鼓励学生自己概括出函数的定义. 生:认真体会4个问题的共同点,然后归纳概括出函数的定义并在全班进行交流. 师:(1)板书函数的定义; (2)强调:①对的理解:作为一个整体,它是一种符号,它可以是解析式(如问题1、2),也可以是图象(如问题3),也可以是表格(如问题4).②定义中,是非空的实数集.③对于的每一个值,按照某种确定的对应关系,都有唯一的值和它对应. 利用前面的分析,进行必要的抽象概括,得到函数的定义,培养学生的归纳、概括能力,提升数学抽象素养.同时剖析概念,使学生抓住概念本质,便于理解记忆.
应用举例 1.一次函数的定义域为,值域也为,对应关系把中的任意一个数,对应到中唯一确定的数. 2.二次函数的定义域为,值域是.当时,;当时, .对应关系把中的任意一个数,对应到中唯一确定的数. 3.反比例函数的定义域为,值域为,对应关系把中的任意一个数,对应到中唯一确定的数. 4.例 函数的解析式是舍弃问题的实际背景而抽象出来的,它反映了两个量之间的对应关系,可以广泛地用于刻画一类事物中的变量关系和规律. 试构造一个问题情境,使其中的变量关系可以用解析式来描述. 解:把看成二次函数,那么它的定义域是,值域是.对应关系把中的任意一个数,对应到中唯一确定的数. 师:想一想,初中我们学过了哪些函数? 生:一次函数、二次函数和反比例函数. 师:你能说一说,这三个函数的定义域、值域和对应关系分别是什么吗? 生:思考,回答,其他同学补充. 师:试构造一个问题情境,使其中的变量关系可以用解析式来描述.如果再对的取值范围作出限制,比如呢? 生:尝试构建一些问题情境,然后相互交流、讨论. 师:针对学生的回答进行点评. 引导学生用函数的定义去理解学过的一次函数、二次函数和反比例函数,比较描述性定义与对应语言刻画的定义,加深对函数概念的理解. 引导学生探讨从具体问题情境中抽象出数学模型,以及通过函数解析式去构建问题情境,加深对函数概念的理解.提升学生数学抽象及数学建模素养.
归纳小结 1.函数的概念. 2.三要素. 学生思考、回答,其他同学补充,教师记录、点评.
布置作业 1.教材第63页练习:第1题. 2.教材第64页练习:第4题.
板书设计
第1课时 函数的概念 1.函数的概念 2.函数三要素 定义域 对应关系 值域 问题1 问题2 问题3 问题4 例 小结 1.函数的概念 2.三要素 作业
教学研讨
教材通过集合语言和对应关系刻画函数概念,并建立完整的函数概念,为什么要强调函数是非零实数集合之间的对应关系呢?这个问题有没有必要跟学生解释清楚呢?如果有必要,那什么时候解析比较恰当呢?这些都是值得课后继续探讨的问题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
