十九章 平行四边形的判定一[下学期]
文档属性
| 名称 | 十九章 平行四边形的判定一[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 104.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-25 09:05:00 | ||
图片预览



文档简介
课件18张PPT。平行四边形的判定一平行四边形☆定义:两组对边分别 的四边形是平行四边形。☆性质:
1、平行四边形对边
2、平行四边形对角
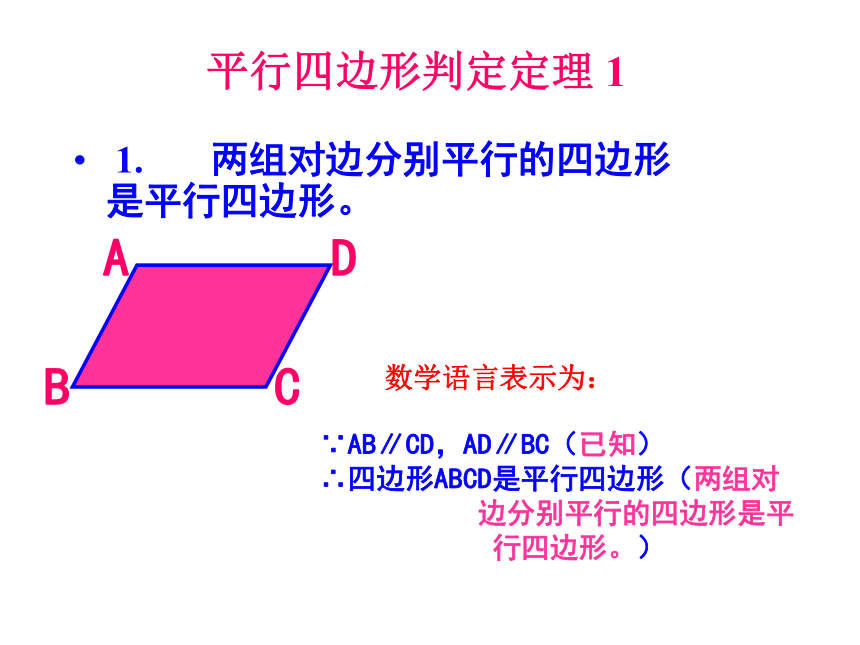
3、平行四边形对角线平行相等互相平分相等4、平行四边形是中心对称图形平行四边形判定定理 1 1. 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对
边分别平行的四边形是平
行四边形。) 数学语言表示为: 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
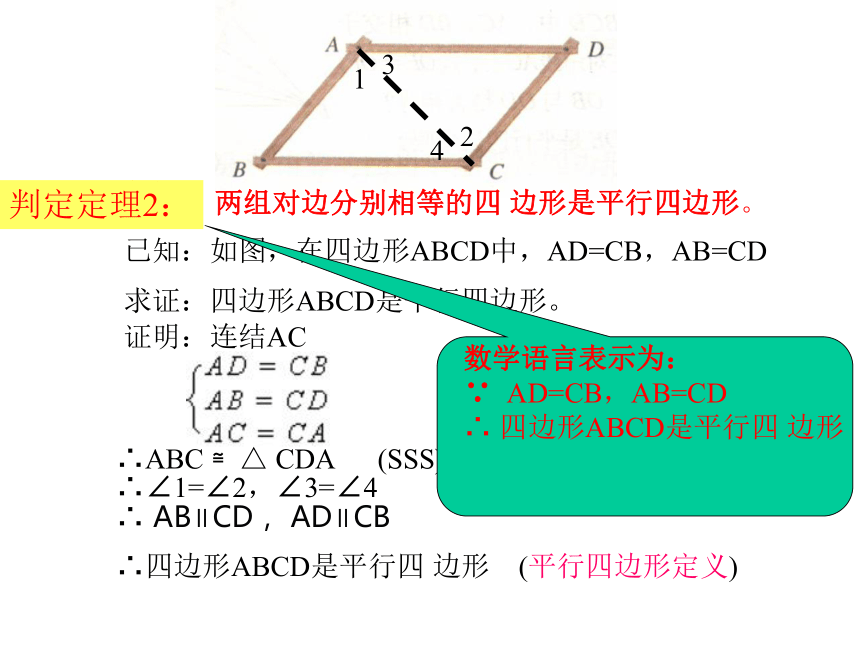
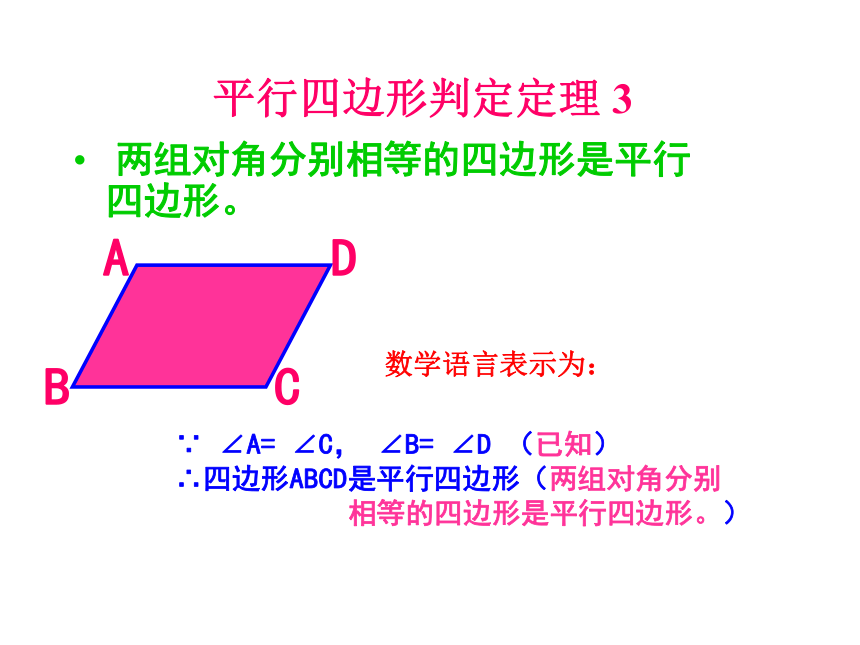
大家都困惑了……请你帮忙猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形ABCD中,AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS) ∴∠1=∠2,∠3=∠41234∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义)判定定理2:平行四边形判定定理 3 两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别
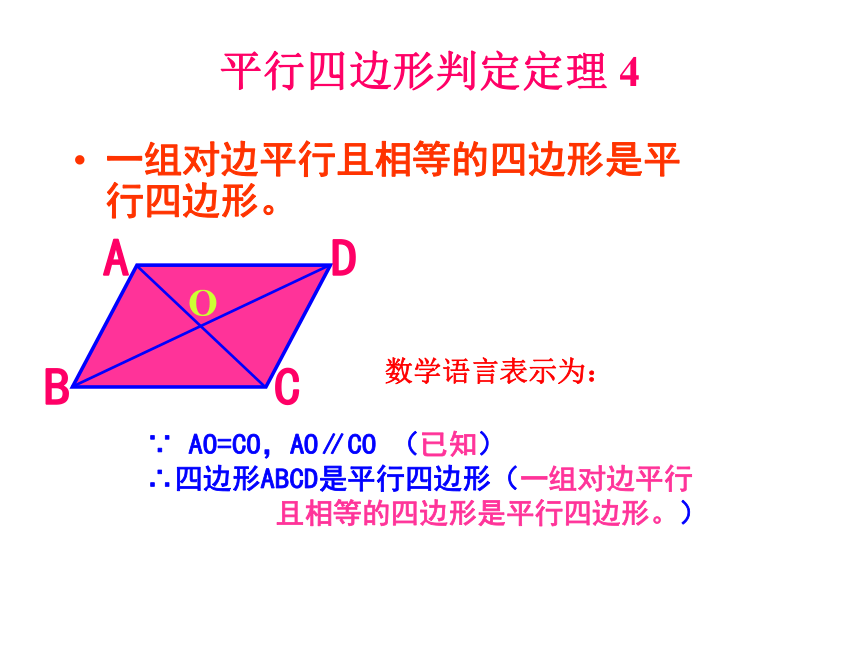
相等的四边形是平行四边形。)数学语言表示为:平行四边形判定定理 4一组对边平行且相等的四边形是平行四边形。 ∵ AO=CO,AO∥CO (已知)
∴四边形ABCD是平行四边形(一组对边平行
且相等的四边形是平行四边形。)O数学语言表示为:对角线互相平分的四边形是平行四边形。已知:如图,四边形ABCD的对角线AC,BD相交于点O,
并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
你能根据上述判定定理证明平行四边形判定定理 5例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.创新训练:(1)一组对边平行,一组对边相等的四边形是平行四边形吗?
(2)一组对边相等,一组对角相等的四边形是平行四边形吗?使学生明白假命题应举反例说明。
两道练习一方面求同,另一方面求异,提高学生素质能力。(3)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?一组对边平行,另一组对边相等的四边形一定是平行四边形吗? 不一定。如等腰梯形。一组对边相等,一组对角
相等的四边形是平行四边形吗?
有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗? 不一定。如右图1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。5、对角线互相平分的四边形是平行四边形。 3、两组对角分别相等的四边形是平行四边形4 、一组对边平行且相等的四边形是平行四边形。练习1: 如图, AB = CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗? 思 考 练习2:如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试说明四边形AFCE是平行四边形。CBDAFE练习3:如图在 ABCD中,E、F、G、H分别是各边上 的点,且AE=CF,BG=DH ,求证:EF与GH互相平分。1、在四边形ABCD中,从(1)AB∥ CD,(2)BC ∥ AD (3)AB=CD(4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )
A 3种 B 4种 C 5种 D 6种
2、不能判定四边形ABCD是平行四边形的条件是( )
A .AB=CD AD=BC B .AB∥CD AB=CD
C.AB=CD AD∥BC C.AB∥CD AD∥ BC
1、平行四边形对边
2、平行四边形对角
3、平行四边形对角线平行相等互相平分相等4、平行四边形是中心对称图形平行四边形判定定理 1 1. 两组对边分别平行的四边形是平行四边形。 ∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对
边分别平行的四边形是平
行四边形。) 数学语言表示为: 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙猜想:两组对边分别相等的四 边形是平行四边形。 已知:如图,在四边形ABCD中,AD=CB,AB=CD求证:四边形ABCD是平行四边形。证明:连结AC∴ABC ≌△ CDA (SSS) ∴∠1=∠2,∠3=∠41234∴ AB∥CD, AD∥CB∴四边形ABCD是平行四 边形 (平行四边形定义)判定定理2:平行四边形判定定理 3 两组对角分别相等的四边形是平行四边形。 ∵ ∠A= ∠C, ∠B= ∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别
相等的四边形是平行四边形。)数学语言表示为:平行四边形判定定理 4一组对边平行且相等的四边形是平行四边形。 ∵ AO=CO,AO∥CO (已知)
∴四边形ABCD是平行四边形(一组对边平行
且相等的四边形是平行四边形。)O数学语言表示为:对角线互相平分的四边形是平行四边形。已知:如图,四边形ABCD的对角线AC,BD相交于点O,
并且 AO=CO,BO=DO。求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
你能根据上述判定定理证明平行四边形判定定理 5例1: 已知:如图 ,E、F是平行四边形ABCD对角线AC
上的两点,并且 AE=CF。
求证:四边形BFDE是平行四边形。证明:连结BD,交AC于点O∵四边形ABCD是平行四边形∴AO=CO ,BO=DO∵AE=CF ∴EO=FO∵BO=DO∴四边形BFDE是平行四边形 (对角线互相平分
的四边形是平行四边形)延长线上的两点,且E.F是OA.OC的中点.上的两点,且DE⊥OA.BF⊥OC.创新训练:(1)一组对边平行,一组对边相等的四边形是平行四边形吗?
(2)一组对边相等,一组对角相等的四边形是平行四边形吗?使学生明白假命题应举反例说明。
两道练习一方面求同,另一方面求异,提高学生素质能力。(3)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗?一组对边平行,另一组对边相等的四边形一定是平行四边形吗? 不一定。如等腰梯形。一组对边相等,一组对角
相等的四边形是平行四边形吗?
有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形吗? 不一定。如右图1、两组对边分别平行的四边形是平行四边形。平行四边形的判定方法2、两组对边分别相等的四边形是平行四边形。5、对角线互相平分的四边形是平行四边形。 3、两组对角分别相等的四边形是平行四边形4 、一组对边平行且相等的四边形是平行四边形。练习1: 如图, AB = CD, 且∠DCA=∠BAC, 四边形ABCD是平行四边形吗? 思 考 练习2:如图,在 ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试说明四边形AFCE是平行四边形。CBDAFE练习3:如图在 ABCD中,E、F、G、H分别是各边上 的点,且AE=CF,BG=DH ,求证:EF与GH互相平分。1、在四边形ABCD中,从(1)AB∥ CD,(2)BC ∥ AD (3)AB=CD(4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )
A 3种 B 4种 C 5种 D 6种
2、不能判定四边形ABCD是平行四边形的条件是( )
A .AB=CD AD=BC B .AB∥CD AB=CD
C.AB=CD AD∥BC C.AB∥CD AD∥ BC
