高中数学必修第一册人教A版(2019)3.1.2_函数的表示法_ 课件(共30张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)3.1.2_函数的表示法_ 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 981.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
人教A 版必修第一册
第三章 函数的概念与性质
3.1.2 函数的表示法
课程目标
1、明确函数的三种表示方法;
2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
3、通过具体实例,了解简单的分段函数,并能简单应用.
数学学科素养
1.数学抽象:函数解析法及能由条件求出解析式;
2.逻辑推理:由条件求函数解析式;
3.数学运算:由函数解析式求值及函数解析式的计算;
4.数据分析:利用图像表示函数;
5.数学建模:由实际问题构建合理的函数模型。
自主预习,回答问题
阅读课本67-68页,思考并完成以下问题
1.表示两个变量之间函数关系的方法有几种?分别是什么?
2.函数的各种表示法各有什么特点?
3.什么是分段函数?分段函数是一个还是几个函数?
4.怎样求分段函数的值?如何画分段函数的图象?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
列表法 图像法 解析法
定 义 用表格的形式把两个变量间的函数关系表示出来的方法 用图像把两个变量间的函数关系表示出来的方法 一个函数的对应关系可以用自变量的解析式表示出来的方法
优 点 不必通过计算就能知道两个变量之间的对应关系,比较 直观 可以 直观地表示函数的局部变化规律,进而可以预测它的整体趋势 能叫便利地通过计算等手段研究函数性质
缺 点 只能表示有限个元素的函数关系 有些函数的图像难以精确作出 一些实际问题难以找到它的解析式
题型分析 举一反三
题型一 函数的表示法
例1
某种笔记本的单价是5元,买x (x∈{1,2, 3,4,5})个
笔记本需要y元.试用三种表示法表示函数y=f(x) .
解:这个函数的定义域是数集{1,2, 3,4,5}.
用解析法可将函数y=f(x)表示为 y=5x, x∈{1,2, 3,4,5}
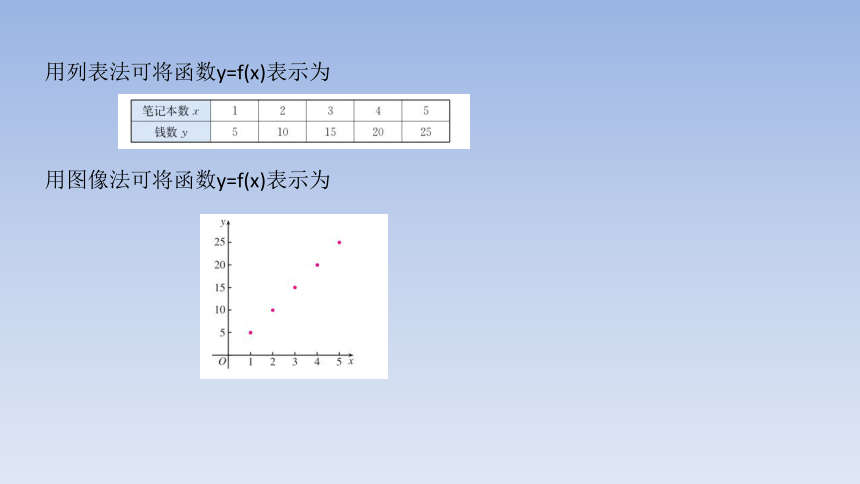
用列表法可将函数y=f(x)表示为
用图像法可将函数y=f(x)表示为
解题方法(表示函数的注意事项)
1. 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;
2. 解析法:必须注明函数的定义域;
3 .图象法:是否连线;
4. 列表法:选取的自变量要有代表性,应能反映定义域的特征.
题型二 分段函数求值
例2:已知函数f (x)=
(1)求f 的值;
(2)若f(x)= ,求x的值.
解题方法(分段函数求值问题)
1.求分段函数的函数值的方法
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,直到求出值为止.当出现 的形式时,应从内到外依次求值.
2.求某条件下自变量的值的方法先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
[跟踪训练二]
1.
题型三 求函数解析式
例3 .(1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;
(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).
解:(1)(方法一)令x+1=t,则x=t-1.
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
∴f(x)=x2-5x+6.
(方法二)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.
(2)设所求的二次函数为f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x对任意的x∈R都成立,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
即2ax+a+b=2x,由恒等式的性质,得
∴∴所求二次函数为f(x)=x2-x+1.
(3)∵对于任意的x都有f(x)+2f(-x)=3x-2,
∴将x替换为-x,得f(-x)+2f(x)=-3x-2,联立方程组消去f(-x),可得f(x)=-3x- .
解题方法(求函数解析式的四种常用方法)
1.直接法(代入法):已知f(x)的解析式,求f(g(x))的解析式,直接将g(x)代入即可.
2.待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程(或方程组),通过解方程(组)求出待定系数,进而求出函数解析式.
3.换元法(有时可用“配凑法”):已知函数f(g(x))的解析式求f(x)的解析式可用换元法(或“配凑法”),即令g(x)=t,反解出x,然后代入f(g(x))中求出f(t),从而求出f(x).
4.解方程组法或消元法:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.
1.已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式;
2.已知f(+1)=x+2,求f(x)的解析式;
3.设函数f(x)满足f(x)+2f=x(x≠0),求f(x).
解:(1)∵f(x)为一次函数,
∴可设f(x)=ax+b(a≠0).
∵f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=2x-1.
∴解得
故f(x)=x+1-或f(x)=-x+1+.
(2)(方法一)f(+1)=()2+2+1-1=(+1)2-1,其中+1≥1,
故所求函数的解析式为f(x)=x2-1,其中x≥1.
(方法二)令+1=t,则x=(t-1)2,且t≥1,
函数f(+1)=x+2可化为f(t)=(t-1)2+2(t-1)=t2-1,故所求函数的解析式为f(x)=x2-1,其中x≥1.
(3)因为对任意的x∈R,且x≠0都有f(x)+2f=x成立,
所以对于∈R,且≠0,有f+2f(x)=,
两式组成方程组
②×2-①得,f(x)=.
题型四 函数的图像及应用
例4 1. 函数f(x)=|x-1|的图象是( )
2.给定函数,
(1)在同一直角坐标系中画出函数的图像;
(2)
.请分别用图像法和解析法表示函数.
解:(1)同一直角坐标系中函数的图像
(2)结合的定义,可得函数的图像
由
解得.
由图易知的解析式为
=
解题方法(函数图像问题处理措施)
(1)若y=f(x)是已学过的基本初等函数,则描出图象上的几个关键点,直接画出图象即可,有些可能需要根据定义域进行取舍.
(2)若y=f(x)不是所学过的基本初等函数之一,则要按:①列表;②描点;③连线三个基本步骤作出y=f(x)的图象.
(3)作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
题型五 函数的实际应用
例5
第一次 第二次 第三次 第四次 第五次 第六次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平均分 88.2 78.3 85.4 80.3 75.7 82.6
下表是某校高一(1)班三位同学在高一学年度几次数学
测试的成绩及班级及班级平均分表:
请你对这三们同学在高一学年度的数学学习情况做一个分析.
解:从表可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况。如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图3.1-6,那么就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
从图3.1-6可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
人教A 版必修第一册
第三章 函数的概念与性质
3.1.2 函数的表示法
课程目标
1、明确函数的三种表示方法;
2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
3、通过具体实例,了解简单的分段函数,并能简单应用.
数学学科素养
1.数学抽象:函数解析法及能由条件求出解析式;
2.逻辑推理:由条件求函数解析式;
3.数学运算:由函数解析式求值及函数解析式的计算;
4.数据分析:利用图像表示函数;
5.数学建模:由实际问题构建合理的函数模型。
自主预习,回答问题
阅读课本67-68页,思考并完成以下问题
1.表示两个变量之间函数关系的方法有几种?分别是什么?
2.函数的各种表示法各有什么特点?
3.什么是分段函数?分段函数是一个还是几个函数?
4.怎样求分段函数的值?如何画分段函数的图象?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
列表法 图像法 解析法
定 义 用表格的形式把两个变量间的函数关系表示出来的方法 用图像把两个变量间的函数关系表示出来的方法 一个函数的对应关系可以用自变量的解析式表示出来的方法
优 点 不必通过计算就能知道两个变量之间的对应关系,比较 直观 可以 直观地表示函数的局部变化规律,进而可以预测它的整体趋势 能叫便利地通过计算等手段研究函数性质
缺 点 只能表示有限个元素的函数关系 有些函数的图像难以精确作出 一些实际问题难以找到它的解析式
题型分析 举一反三
题型一 函数的表示法
例1
某种笔记本的单价是5元,买x (x∈{1,2, 3,4,5})个
笔记本需要y元.试用三种表示法表示函数y=f(x) .
解:这个函数的定义域是数集{1,2, 3,4,5}.
用解析法可将函数y=f(x)表示为 y=5x, x∈{1,2, 3,4,5}
用列表法可将函数y=f(x)表示为
用图像法可将函数y=f(x)表示为
解题方法(表示函数的注意事项)
1. 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;
2. 解析法:必须注明函数的定义域;
3 .图象法:是否连线;
4. 列表法:选取的自变量要有代表性,应能反映定义域的特征.
题型二 分段函数求值
例2:已知函数f (x)=
(1)求f 的值;
(2)若f(x)= ,求x的值.
解题方法(分段函数求值问题)
1.求分段函数的函数值的方法
(1)确定要求值的自变量属于哪一段区间.
(2)代入该段的解析式求值,直到求出值为止.当出现 的形式时,应从内到外依次求值.
2.求某条件下自变量的值的方法先假设所求的值在分段函数定义区间的各段上,然后相应求出自变量的值,切记代入检验.
[跟踪训练二]
1.
题型三 求函数解析式
例3 .(1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;
(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).
解:(1)(方法一)令x+1=t,则x=t-1.
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
∴f(x)=x2-5x+6.
(方法二)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.
(2)设所求的二次函数为f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x对任意的x∈R都成立,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
即2ax+a+b=2x,由恒等式的性质,得
∴∴所求二次函数为f(x)=x2-x+1.
(3)∵对于任意的x都有f(x)+2f(-x)=3x-2,
∴将x替换为-x,得f(-x)+2f(x)=-3x-2,联立方程组消去f(-x),可得f(x)=-3x- .
解题方法(求函数解析式的四种常用方法)
1.直接法(代入法):已知f(x)的解析式,求f(g(x))的解析式,直接将g(x)代入即可.
2.待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程(或方程组),通过解方程(组)求出待定系数,进而求出函数解析式.
3.换元法(有时可用“配凑法”):已知函数f(g(x))的解析式求f(x)的解析式可用换元法(或“配凑法”),即令g(x)=t,反解出x,然后代入f(g(x))中求出f(t),从而求出f(x).
4.解方程组法或消元法:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.
1.已知f(x)是一次函数,且f(f(x))=2x-1,求f(x)的解析式;
2.已知f(+1)=x+2,求f(x)的解析式;
3.设函数f(x)满足f(x)+2f=x(x≠0),求f(x).
解:(1)∵f(x)为一次函数,
∴可设f(x)=ax+b(a≠0).
∵f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b=2x-1.
∴解得
故f(x)=x+1-或f(x)=-x+1+.
(2)(方法一)f(+1)=()2+2+1-1=(+1)2-1,其中+1≥1,
故所求函数的解析式为f(x)=x2-1,其中x≥1.
(方法二)令+1=t,则x=(t-1)2,且t≥1,
函数f(+1)=x+2可化为f(t)=(t-1)2+2(t-1)=t2-1,故所求函数的解析式为f(x)=x2-1,其中x≥1.
(3)因为对任意的x∈R,且x≠0都有f(x)+2f=x成立,
所以对于∈R,且≠0,有f+2f(x)=,
两式组成方程组
②×2-①得,f(x)=.
题型四 函数的图像及应用
例4 1. 函数f(x)=|x-1|的图象是( )
2.给定函数,
(1)在同一直角坐标系中画出函数的图像;
(2)
.请分别用图像法和解析法表示函数.
解:(1)同一直角坐标系中函数的图像
(2)结合的定义,可得函数的图像
由
解得.
由图易知的解析式为
=
解题方法(函数图像问题处理措施)
(1)若y=f(x)是已学过的基本初等函数,则描出图象上的几个关键点,直接画出图象即可,有些可能需要根据定义域进行取舍.
(2)若y=f(x)不是所学过的基本初等函数之一,则要按:①列表;②描点;③连线三个基本步骤作出y=f(x)的图象.
(3)作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
题型五 函数的实际应用
例5
第一次 第二次 第三次 第四次 第五次 第六次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平均分 88.2 78.3 85.4 80.3 75.7 82.6
下表是某校高一(1)班三位同学在高一学年度几次数学
测试的成绩及班级及班级平均分表:
请你对这三们同学在高一学年度的数学学习情况做一个分析.
解:从表可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况。如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图3.1-6,那么就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
从图3.1-6可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
