平行四边形的判定[下学期]
文档属性
| 名称 | 平行四边形的判定[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 167.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-29 00:00:00 | ||
图片预览

文档简介
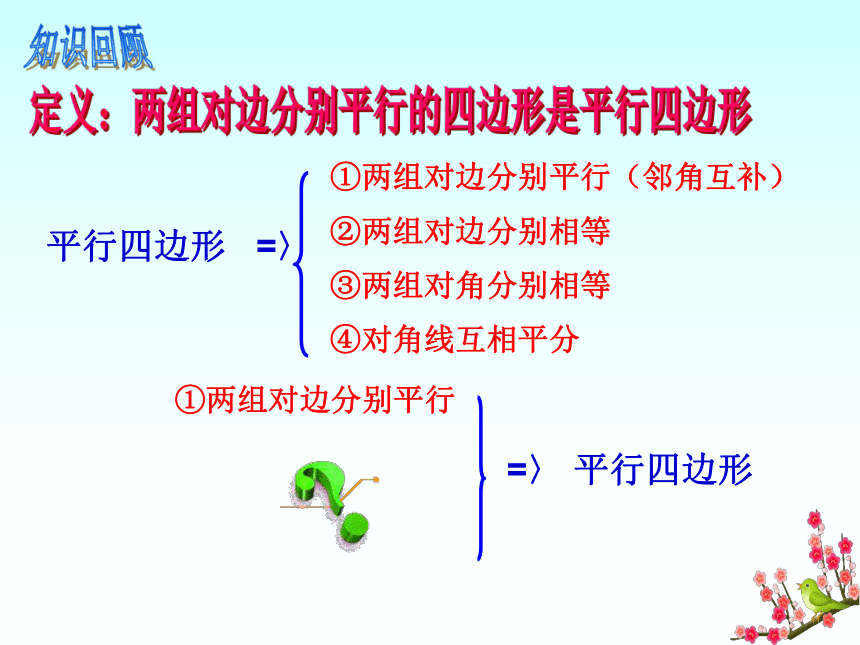
课件13张PPT。平行四边形的判定八年级备课组平行四边形 =〉①两组对边分别平行(邻角互补)②两组对边分别相等③两组对角分别相等④对角线互相平分定义:两组对边分别平行的四边形是平行四边形=〉 平行四边形①两组对边分别平行知识回顾BDAC已知:四边形ABCD, AB=CD,AD=BC
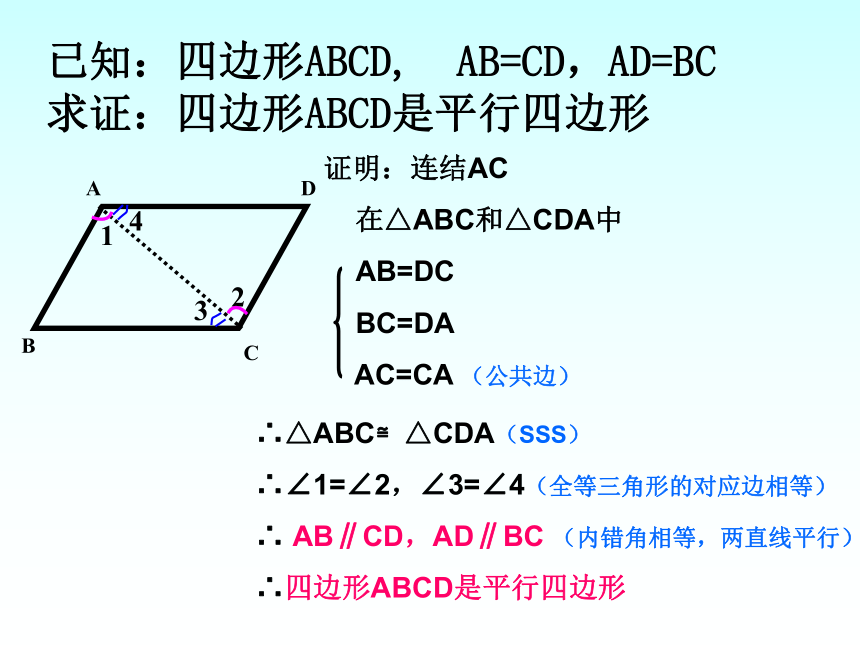
求证:四边形ABCD是平行四边形2134证明:连结AC
在△ABC和△CDA中
AB=DC
BC=DA
AC=CA (公共边)∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
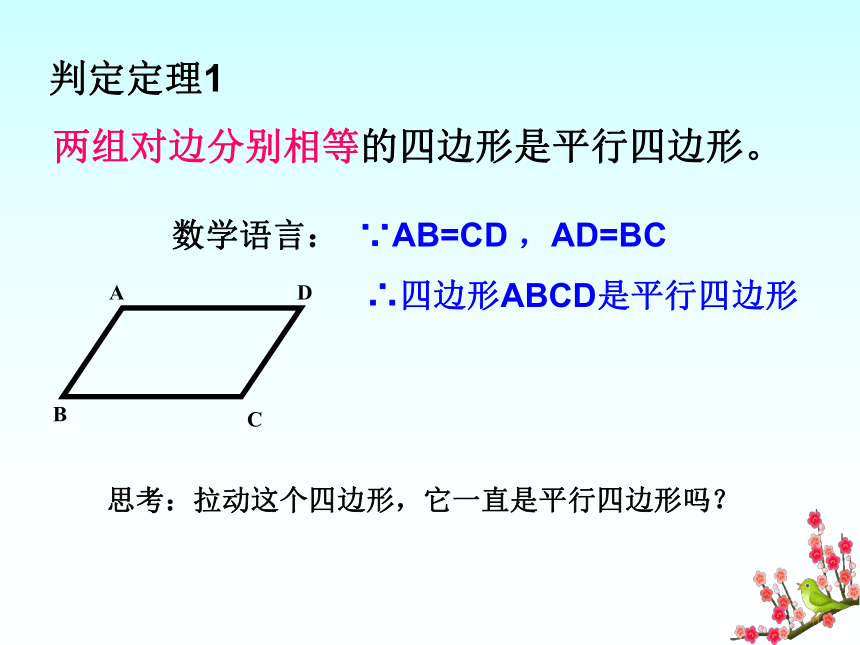
∴四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。判定定理1数学语言: ∵AB=CD ,AD=BC
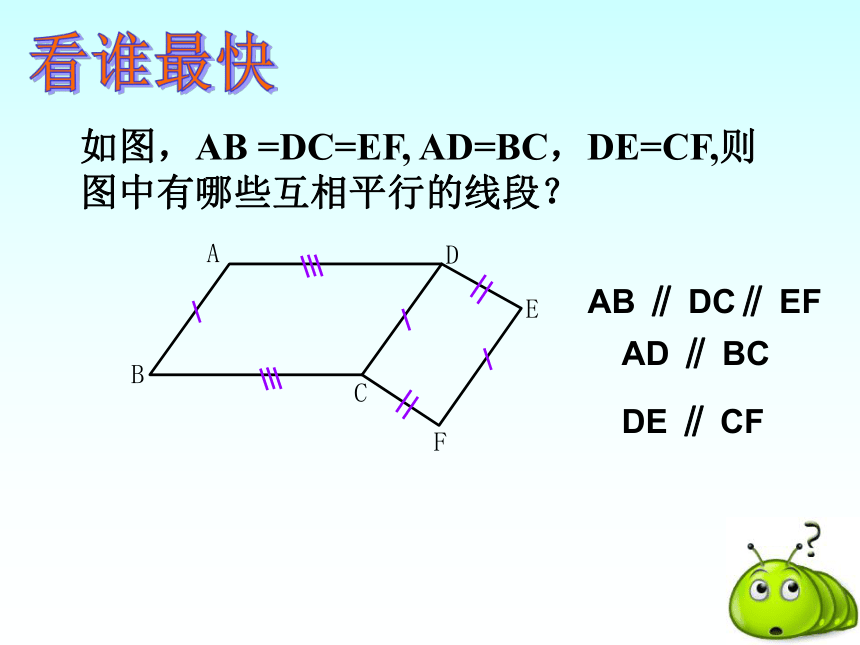
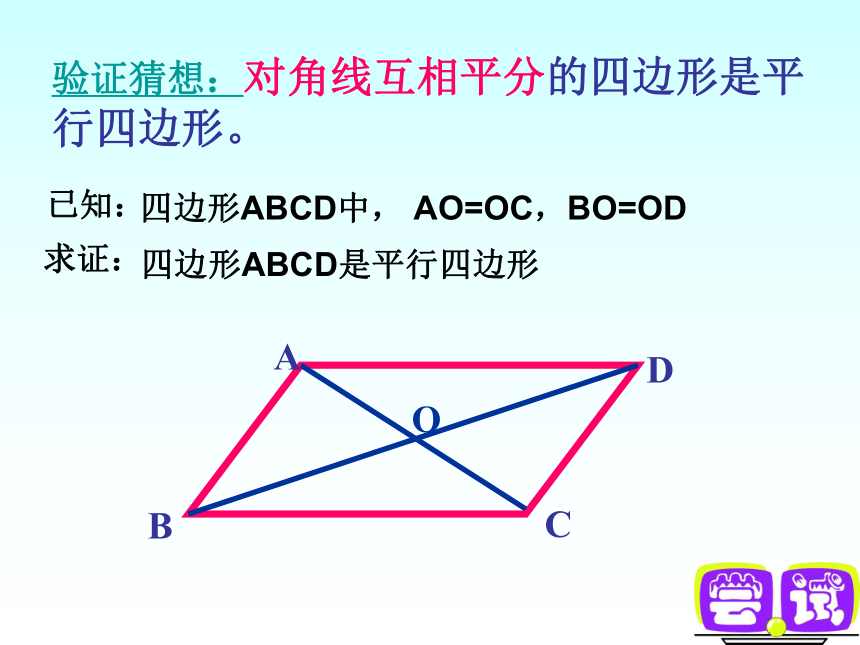
∴四边形ABCD是平行四边形 思考:拉动这个四边形,它一直是平行四边形吗? 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF 验证猜想:对角线互相平分的四边形是平行四边形。四边形ABCD中, AO=OC,BO=OD已知:求证:四边形ABCD是平行四边形已知:四边形ABCD的对角线AC、BD 相交于点O,并且AO = CO ,BO = DO 。
求证:四边形ABCD是平行四边形。证明:∵ AO = CO ,BO = DO ,∠1 = ∠2,∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ Bc ∴四边形ABCD是 平行四边形
(两组对边分别平行的四边形是平行四边形)DABCO1234∴ ∠3 = ∠4对角线互相平分的四边形是平行四边形。判定定理2数学语言:通过证明被确认正确的命题可以作为判定定理使用∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形ABCD如图:AD是ΔABC的边BC边上的中线. 延长AD到点E,使DE=AD,连接BE,CE; 判断四边形ABEC是否平行四边形,并说明理由.看谁最快 例3:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F是AC上的两点,并且AE=CF.求证四边形BFDE是平行四边形。ACBEDFO证明:∵四边形ABCD是平行四边形
∴AO=CO , BO=DO
∵ AE=CF
EO=AO?AE
FO=CO?CF
∴EO=FO
∴四边形BFDE是平行四边形
①有一组对边平行的四边形是平行四边形。
②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。③对角线相等的四边形是平行四边形。④一条对角线平分另一条对角线的四边形是平行四边形。判断题下列四边形是平行四边形吗?为什么?比一比⑴⑶BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝已知:四边形ABCD的对角线AC、BD 相交于点O,并且AO = CO ,BO = DO 。
求证:四边形ABCD是平行四边形。证明:∵ AO = CO ,BO = DO ,∠1 = ∠2,∴△AOB≌△COD∴AB = CD 同理AD =Bc ∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)DABCO12
求证:四边形ABCD是平行四边形2134证明:连结AC
在△ABC和△CDA中
AB=DC
BC=DA
AC=CA (公共边)∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。判定定理1数学语言: ∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形 思考:拉动这个四边形,它一直是平行四边形吗? 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF 验证猜想:对角线互相平分的四边形是平行四边形。四边形ABCD中, AO=OC,BO=OD已知:求证:四边形ABCD是平行四边形已知:四边形ABCD的对角线AC、BD 相交于点O,并且AO = CO ,BO = DO 。
求证:四边形ABCD是平行四边形。证明:∵ AO = CO ,BO = DO ,∠1 = ∠2,∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ Bc ∴四边形ABCD是 平行四边形
(两组对边分别平行的四边形是平行四边形)DABCO1234∴ ∠3 = ∠4对角线互相平分的四边形是平行四边形。判定定理2数学语言:通过证明被确认正确的命题可以作为判定定理使用∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形ABCD如图:AD是ΔABC的边BC边上的中线. 延长AD到点E,使DE=AD,连接BE,CE; 判断四边形ABEC是否平行四边形,并说明理由.看谁最快 例3:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F是AC上的两点,并且AE=CF.求证四边形BFDE是平行四边形。ACBEDFO证明:∵四边形ABCD是平行四边形
∴AO=CO , BO=DO
∵ AE=CF
EO=AO?AE
FO=CO?CF
∴EO=FO
∴四边形BFDE是平行四边形
①有一组对边平行的四边形是平行四边形。
②有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形。③对角线相等的四边形是平行四边形。④一条对角线平分另一条对角线的四边形是平行四边形。判断题下列四边形是平行四边形吗?为什么?比一比⑴⑶BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝已知:四边形ABCD的对角线AC、BD 相交于点O,并且AO = CO ,BO = DO 。
求证:四边形ABCD是平行四边形。证明:∵ AO = CO ,BO = DO ,∠1 = ∠2,∴△AOB≌△COD∴AB = CD 同理AD =Bc ∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)DABCO12
