高中数学必修第一册人教A版(2019)3.2.1《函数的单调性》名师课件(共27张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)3.2.1《函数的单调性》名师课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 16:22:06 | ||
图片预览





文档简介
(共27张PPT)
前面学习了函数的定义和表示法,知道函数)(∈A)描述了客观世界中变量之间的一种对应关系.这样,我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律,因此,研究函数的性质,如随着自变量的增大函数值是增大还是减小,有没有最大值或最小值,函数图象有什么特征等,是认识客观规律的重要方法.
复习引入
人教A版同步教材名师课件
函数的单调性
学习目标
学 习 目 标 核心素养
借助函数的图象加深对函数概念的理解 数学抽象
能够用定义判断或证明函数的单调性,会求一些简单函数的单调区间 逻辑推理
理解函数最大(小)值的含义,会利用函数单调性求最值 直观想象
学习目标
课程目标
1.理解增函数、减函数的概念及函数单调性的定义;
2.会根据单调定义证明函数单调性;
3.理解函数的最大(小)值及其几何意义;
4.学会运用函数图象理解和研究函数的性质.
数学学科素养
1.数学抽象:用数学语言表示函数单调性和最值;
2.逻辑推理:证明函数单调性;
3.数学运算:运用单调性解决不等式;
4.数据分析:利用图像求单调区间和最值;
5.数学建模:在具体问题情境中运用单调性和最值解决实际问题.
探究新知
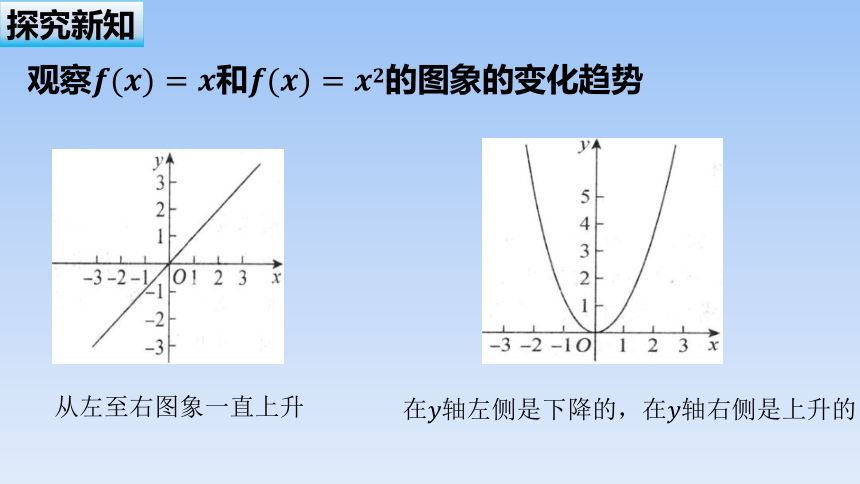
观察和的图象的变化趋势
从左至右图象一直上升
在轴左侧是下降的,在轴右侧是上升的
函数图象的“上升”“下降”反映了函数的一个基本性质,这种性质称为函数的单调性.如何描述函数图象的“上升”和“下降”呢?
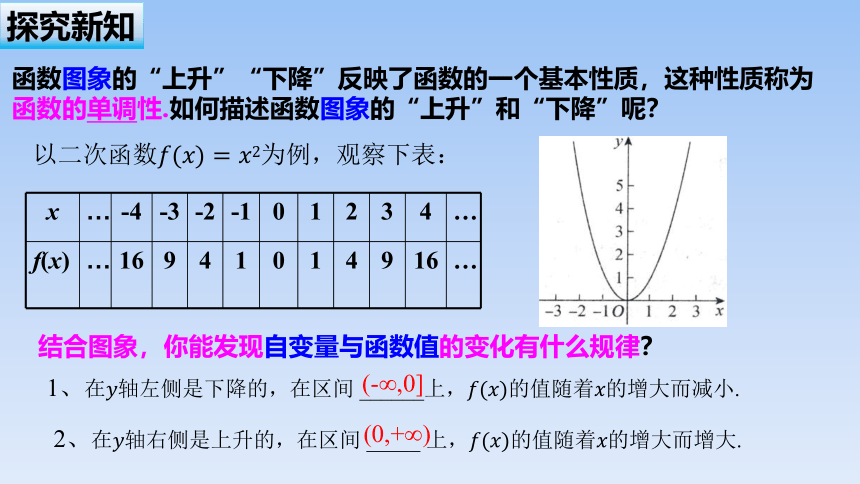
以二次函数为例,观察下表:
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x) … 16 9 4 1 0 1 4 9 16 …
结合图象,你能发现自变量与函数值的变化有什么规律?
探究新知
1、在轴左侧是下降的,在区间 ______上,的值随着的增大而减小.
2、在轴右侧是上升的,在区间 _____ 上,的值随着的增大而增大.
(-∞,0]
(0,+∞)
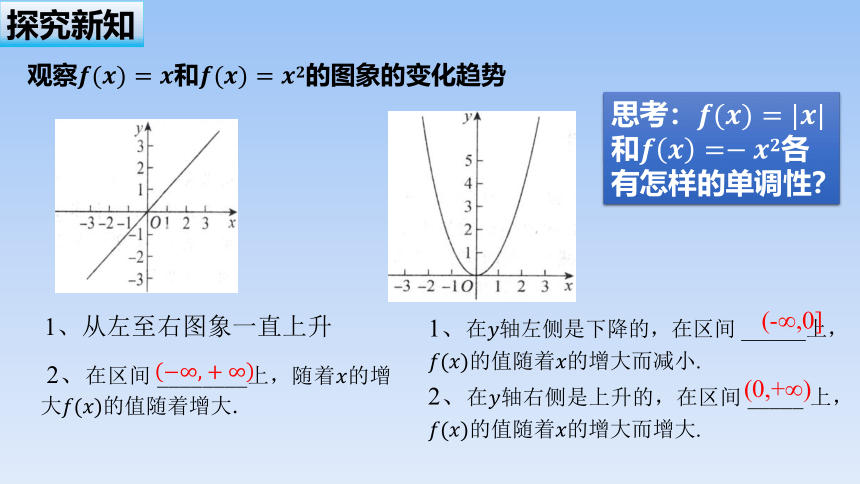
观察和的图象的变化趋势
2、在区间 ________上,随着的增大的值随着增大.
1、从左至右图象一直上升
1、在轴左侧是下降的,在区间 ______上,的值随着的增大而减小.
2、在轴右侧是上升的,在区间 _____ 上,的值随着的增大而增大.
(-∞,0]
(0,+∞)
思考:和各有怎样的单调性?
探究新知
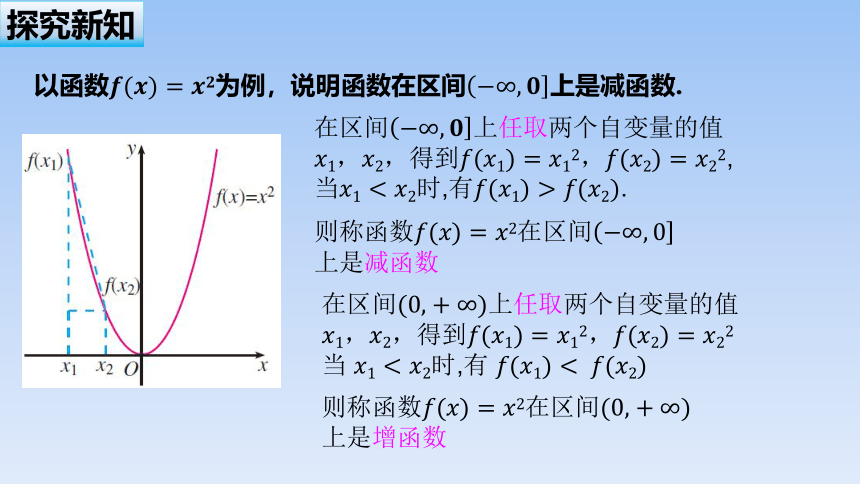
在区间上任取两个自变量的值得到当 时,有
在区间上任取两个自变量的值得到, 当时,有.
则称函数在区间上是增函数
则称函数在区间上是减函数
探究新知
以函数为例,说明函数在区间上是减函数.
增函数
一般地,设函数的定义域为,
如果对于定义域内某个区间内的 两个自变量的值,
当时,都有 那么就说在区间D上是增函数,
任意
探究新知
定义中有三个特征:①属于同一个区间;②是任意两个实数,不能取两个特殊值代替;③有大小关系.
如果函数在区间上是增函数或是减函数,那么就说函数在这一区间具有(严格的)单调性,区间叫做的单调区间.
如果对于定义域内某个区间内的 两个自变量的值, ,
当时,都有 那么就说在区间D上是减函数。
任意
减函数
探究新知
探究新知
观察函数的图象,完成下列思考.
思考1:反比例函数的图象如图,它在区间和上都是减函数,能否说它在定义域上是减函数?为什么?
不能,显然时,满足,但不成立.
思考2:如果函数存在单调区间,那么函数是单调函数吗?
不能,当函数出现两个以上单调区间时,单调区间之间可以用“,”分开,也可以用“和”来表示,但不能使用“∪”.
探究新知
若函数在区间上具有单调性,则在区间上具有以下性质:
(1) 与( 为常数)具有相同的单调性.
(2)当时, 与具有相同的单调性;当时, 与具有相反的单调性.
(3)若恒为正值或恒为负值,则当时,与具有相反的单调性;当时,与具有相同的单调性.
(4)若0,则与具有相同的单调性.
(5)当都是增(减)函数时,若两者都恒大于零,则也是增(减)函数;若两者都恒小于零,则是减(增)函数.
典例讲解
例1.下列命题正确的是
解析
D
A.定义在上的函数若存在,当时,有,那么在上为增函数
B.定义在上的函数若有无穷多对,当时,有,那么在上为增函数
C.若函数在区间上为减函数,在区间上也是减函数,那么在上一定是减函数
D.若函数区间上的增函数,且(),则
A项中,并不是对任意都成立,故A错;B项中,虽然有无穷多对,但也不能代表“所有”“任意”,故B错;C项中,以为例,虽然在和上均为减函数,但在整个定义域上却不具有单调性,故C错,故选D.
典例讲解
例2.根据定义,研究函数的单调性
解析
思路分析
根据函数单调性的定义,需要考察当时,还是.根据实数大小关系的基本事实,只要考察与0的大小关系.
函数的定义域是R.,则
由,得<0.所以
①当时,.
于是 ,即
这时, 是增函数.
②当时,.
于是 ,即
这时, 是减函数.
典例讲解
例3.判断函数在区间上的单调性,并用单调
性的定义证明.
解析
函数在区间上单调递减.
任取, ∈ ,且,
则
∵ , ∈ ,且,
,由单调性的定义可知函数在区间上单调递减.
方法归纳
用定义法证明和判断函数的单调性
定义法证明函数单调性的四个步骤:
在证明函数的单调性时,我们还可以利用其等价式子:任取,那么
在上是增函数;
在上是减函数.
方法归纳
变式训练
1.证明:函数在 上是减函数.
任取∈,且,
证明
则
在∈R上恒成立,
在 上是减函数.
变式训练
分析
2.对于任意的,给出下列条件:
① ;② ③ ;
④ ⑤ ;
⑥ .
能判断在上为增函数的是函数的是 ;为减函数的是 .
由增函数、减函数的定义及不等式的性质,只要能判定对任意的, 若,就可以判定在上为增函数;若,就可以判定在上为减函数.故①③⑤为增函数,②④⑥为减函数.
①③⑤ ②④⑥
典例讲解
例4.求下列函数的单调区间:
解析
思路分析
去掉绝对值符号,转化成分段函数的形式,画出函数图象,根据图象直接写出单调区间.首先配方整理,再画出函数图象,根据图象直接写出单调区间.
图象如图所示:
的单调递减区间为],单调递增区间为+).
典例讲解
例4.求下列函数的单调区间:
解析
思路分析
去掉绝对值符号,转化成分段函数的形式,画出函数图象,根据图象直接写出单调区间.首先配方整理,再画出函数图象,根据图象直接写出单调区间.
令.
先画出的图象,保留其在轴及轴上方部分,把它在轴下方的图象翻到轴上方就得到的图象,如图所示.
由图象易得:函数的递增区间是;函数的递减区间是
(1)利用函数图象确定函数的单调区间,具体做法是先化简函数解析式,再画出它的草图,最后根据函数的定义域并结合草图,确定函数的单调区间.
(2)当函数的解析式中含有绝对值时,可以利用分界点讨论,去掉绝对值符号,将函数转化为分段函数,然后画出函数的图象,通过观察函数图象得到函数的单调区间.
方法归纳
变式训练
3.求下列函数的单调区间:
.
分析
作出函数图象如图所示.
由图象可知,函数的单调减区间是,单调增区间是.
变式训练
3.求下列函数的单调区间:
.
分析
作出函数图象如图所示.
由图象可知,函数的单调增区间是, [0,1]单调减区间是.
一般地,设函数的定义域为,
如果对于定义域内某个区间内的任意两个自变量的值,当时,都有 那么就说在区间D上是增函数;如果对于定义域内某个区间内的任意两个自变量的值, , 当时,都有 那么就说在区间D上是减函数.
定义中有三个特征:①属于同一个区间;②是任意两个实数,不能取两个特殊值代替;③有大小关系.
增、减函数
归纳小结
用定义法证明和判断函数的单调性
定义法证明函数单调性的四个步骤:
归纳小结
作 业
课本P86复习巩固:3
综合运用:8
前面学习了函数的定义和表示法,知道函数)(∈A)描述了客观世界中变量之间的一种对应关系.这样,我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律,因此,研究函数的性质,如随着自变量的增大函数值是增大还是减小,有没有最大值或最小值,函数图象有什么特征等,是认识客观规律的重要方法.
复习引入
人教A版同步教材名师课件
函数的单调性
学习目标
学 习 目 标 核心素养
借助函数的图象加深对函数概念的理解 数学抽象
能够用定义判断或证明函数的单调性,会求一些简单函数的单调区间 逻辑推理
理解函数最大(小)值的含义,会利用函数单调性求最值 直观想象
学习目标
课程目标
1.理解增函数、减函数的概念及函数单调性的定义;
2.会根据单调定义证明函数单调性;
3.理解函数的最大(小)值及其几何意义;
4.学会运用函数图象理解和研究函数的性质.
数学学科素养
1.数学抽象:用数学语言表示函数单调性和最值;
2.逻辑推理:证明函数单调性;
3.数学运算:运用单调性解决不等式;
4.数据分析:利用图像求单调区间和最值;
5.数学建模:在具体问题情境中运用单调性和最值解决实际问题.
探究新知
观察和的图象的变化趋势
从左至右图象一直上升
在轴左侧是下降的,在轴右侧是上升的
函数图象的“上升”“下降”反映了函数的一个基本性质,这种性质称为函数的单调性.如何描述函数图象的“上升”和“下降”呢?
以二次函数为例,观察下表:
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x) … 16 9 4 1 0 1 4 9 16 …
结合图象,你能发现自变量与函数值的变化有什么规律?
探究新知
1、在轴左侧是下降的,在区间 ______上,的值随着的增大而减小.
2、在轴右侧是上升的,在区间 _____ 上,的值随着的增大而增大.
(-∞,0]
(0,+∞)
观察和的图象的变化趋势
2、在区间 ________上,随着的增大的值随着增大.
1、从左至右图象一直上升
1、在轴左侧是下降的,在区间 ______上,的值随着的增大而减小.
2、在轴右侧是上升的,在区间 _____ 上,的值随着的增大而增大.
(-∞,0]
(0,+∞)
思考:和各有怎样的单调性?
探究新知
在区间上任取两个自变量的值得到当 时,有
在区间上任取两个自变量的值得到, 当时,有.
则称函数在区间上是增函数
则称函数在区间上是减函数
探究新知
以函数为例,说明函数在区间上是减函数.
增函数
一般地,设函数的定义域为,
如果对于定义域内某个区间内的 两个自变量的值,
当时,都有 那么就说在区间D上是增函数,
任意
探究新知
定义中有三个特征:①属于同一个区间;②是任意两个实数,不能取两个特殊值代替;③有大小关系.
如果函数在区间上是增函数或是减函数,那么就说函数在这一区间具有(严格的)单调性,区间叫做的单调区间.
如果对于定义域内某个区间内的 两个自变量的值, ,
当时,都有 那么就说在区间D上是减函数。
任意
减函数
探究新知
探究新知
观察函数的图象,完成下列思考.
思考1:反比例函数的图象如图,它在区间和上都是减函数,能否说它在定义域上是减函数?为什么?
不能,显然时,满足,但不成立.
思考2:如果函数存在单调区间,那么函数是单调函数吗?
不能,当函数出现两个以上单调区间时,单调区间之间可以用“,”分开,也可以用“和”来表示,但不能使用“∪”.
探究新知
若函数在区间上具有单调性,则在区间上具有以下性质:
(1) 与( 为常数)具有相同的单调性.
(2)当时, 与具有相同的单调性;当时, 与具有相反的单调性.
(3)若恒为正值或恒为负值,则当时,与具有相反的单调性;当时,与具有相同的单调性.
(4)若0,则与具有相同的单调性.
(5)当都是增(减)函数时,若两者都恒大于零,则也是增(减)函数;若两者都恒小于零,则是减(增)函数.
典例讲解
例1.下列命题正确的是
解析
D
A.定义在上的函数若存在,当时,有,那么在上为增函数
B.定义在上的函数若有无穷多对,当时,有,那么在上为增函数
C.若函数在区间上为减函数,在区间上也是减函数,那么在上一定是减函数
D.若函数区间上的增函数,且(),则
A项中,并不是对任意都成立,故A错;B项中,虽然有无穷多对,但也不能代表“所有”“任意”,故B错;C项中,以为例,虽然在和上均为减函数,但在整个定义域上却不具有单调性,故C错,故选D.
典例讲解
例2.根据定义,研究函数的单调性
解析
思路分析
根据函数单调性的定义,需要考察当时,还是.根据实数大小关系的基本事实,只要考察与0的大小关系.
函数的定义域是R.,则
由,得<0.所以
①当时,.
于是 ,即
这时, 是增函数.
②当时,.
于是 ,即
这时, 是减函数.
典例讲解
例3.判断函数在区间上的单调性,并用单调
性的定义证明.
解析
函数在区间上单调递减.
任取, ∈ ,且,
则
∵ , ∈ ,且,
,由单调性的定义可知函数在区间上单调递减.
方法归纳
用定义法证明和判断函数的单调性
定义法证明函数单调性的四个步骤:
在证明函数的单调性时,我们还可以利用其等价式子:任取,那么
在上是增函数;
在上是减函数.
方法归纳
变式训练
1.证明:函数在 上是减函数.
任取∈,且,
证明
则
在∈R上恒成立,
在 上是减函数.
变式训练
分析
2.对于任意的,给出下列条件:
① ;② ③ ;
④ ⑤ ;
⑥ .
能判断在上为增函数的是函数的是 ;为减函数的是 .
由增函数、减函数的定义及不等式的性质,只要能判定对任意的, 若,就可以判定在上为增函数;若,就可以判定在上为减函数.故①③⑤为增函数,②④⑥为减函数.
①③⑤ ②④⑥
典例讲解
例4.求下列函数的单调区间:
解析
思路分析
去掉绝对值符号,转化成分段函数的形式,画出函数图象,根据图象直接写出单调区间.首先配方整理,再画出函数图象,根据图象直接写出单调区间.
图象如图所示:
的单调递减区间为],单调递增区间为+).
典例讲解
例4.求下列函数的单调区间:
解析
思路分析
去掉绝对值符号,转化成分段函数的形式,画出函数图象,根据图象直接写出单调区间.首先配方整理,再画出函数图象,根据图象直接写出单调区间.
令.
先画出的图象,保留其在轴及轴上方部分,把它在轴下方的图象翻到轴上方就得到的图象,如图所示.
由图象易得:函数的递增区间是;函数的递减区间是
(1)利用函数图象确定函数的单调区间,具体做法是先化简函数解析式,再画出它的草图,最后根据函数的定义域并结合草图,确定函数的单调区间.
(2)当函数的解析式中含有绝对值时,可以利用分界点讨论,去掉绝对值符号,将函数转化为分段函数,然后画出函数的图象,通过观察函数图象得到函数的单调区间.
方法归纳
变式训练
3.求下列函数的单调区间:
.
分析
作出函数图象如图所示.
由图象可知,函数的单调减区间是,单调增区间是.
变式训练
3.求下列函数的单调区间:
.
分析
作出函数图象如图所示.
由图象可知,函数的单调增区间是, [0,1]单调减区间是.
一般地,设函数的定义域为,
如果对于定义域内某个区间内的任意两个自变量的值,当时,都有 那么就说在区间D上是增函数;如果对于定义域内某个区间内的任意两个自变量的值, , 当时,都有 那么就说在区间D上是减函数.
定义中有三个特征:①属于同一个区间;②是任意两个实数,不能取两个特殊值代替;③有大小关系.
增、减函数
归纳小结
用定义法证明和判断函数的单调性
定义法证明函数单调性的四个步骤:
归纳小结
作 业
课本P86复习巩固:3
综合运用:8
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
