高中数学必修第一册人教A版(2019)《3.2函数的基本性质》教材分析
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)《3.2函数的基本性质》教材分析 |

|
|
| 格式 | docx | ||
| 文件大小 | 489.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 20:57:04 | ||
图片预览



文档简介
3.2函数的基本性质
一、本节知识结构框图
二、重点、难点
重点:函数的单调性、奇偶性.
难点:增(减)函数的定义,利用增(减)函数的定义判断函数的单调性.
三、教科书编写意图及教学建议
运动变化的规律性是性质,变化中的不变性也是性质,函数是刻画客观世界中运动变化的重要数学模型,因此,运动变化中的规律性或不变性通常反映为函数的性质.
高中阶段要研究的函数性质有:单调性、最大(小)值、奇偶性、周期性、函数的零点、正或负增长率(衰减率)、增长(减少)快慢等.本节研究函数的单调性、最大(小)值、奇偶性,其中单调性是函数最重要的性质.
函数的单调性和奇偶性都可以在函数的图象上反映出来.因此,首先借助函数图象对其单调性和奇偶性有一个初步了解,并在此基础上进行定量刻画;然后用数学符号语言形成单调性与奇偶性的定义.这是研究函数性质的一般过程与方法,这样做有利于发展学生的数形结合思想,并由此培养学生数学抽象与直观想象等素养.
在教学时建议从若干实例出发,归纳出共同特征,再概括到同类事物中形成一般性质.这种从特殊到一般的归纳概括过程,有利于培养学生的数学思维和推理论证能力.
3.2.1单调性与最大(小)值
1.函数的单调性
学习函数的单调性,不仅可以让学生加深对函数基本性质的认识,而且可以让学生体会研究函数性质的过程与方法.
教科书给出研究函数单调性的过程是:
具体函数—图象特征—数量刻画—符号语言—抽象定义—单调性判定.
(1)函数单调性的定性刻画
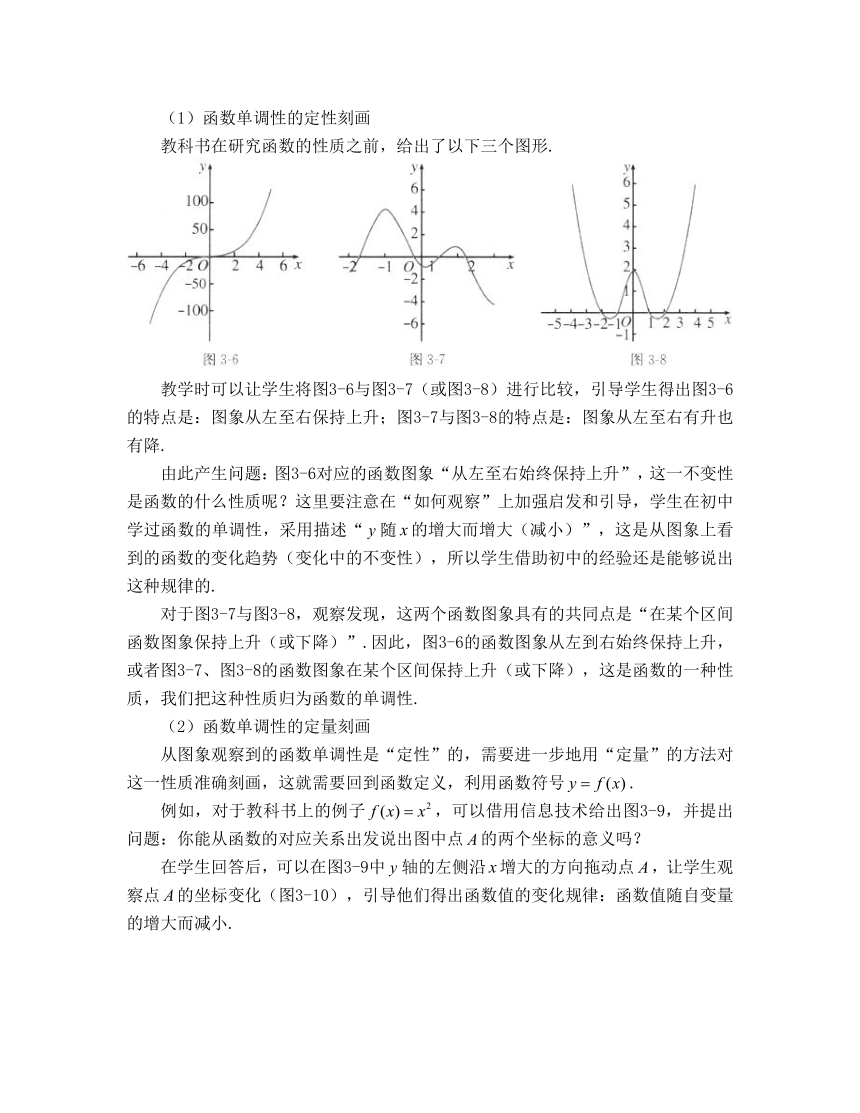
教科书在研究函数的性质之前,给出了以下三个图形.
教学时可以让学生将图3-6与图3-7(或图3-8)进行比较,引导学生得出图3-6的特点是:图象从左至右保持上升;图3-7与图3-8的特点是:图象从左至右有升也有降.
由此产生问题:图3-6对应的函数图象“从左至右始终保持上升”,这一不变性是函数的什么性质呢?这里要注意在“如何观察”上加强启发和引导,学生在初中学过函数的单调性,采用描述“随的增大而增大(减小)”,这是从图象上看到的函数的变化趋势(变化中的不变性),所以学生借助初中的经验还是能够说出这种规律的.
对于图3-7与图3-8,观察发现,这两个函数图象具有的共同点是“在某个区间函数图象保持上升(或下降)”.因此,图3-6的函数图象从左到右始终保持上升,或者图3-7、图3-8的函数图象在某个区间保持上升(或下降),这是函数的一种性质,我们把这种性质归为函数的单调性.
(2)函数单调性的定量刻画
从图象观察到的函数单调性是“定性”的,需要进一步地用“定量”的方法对这一性质准确刻画,这就需要回到函数定义,利用函数符号.
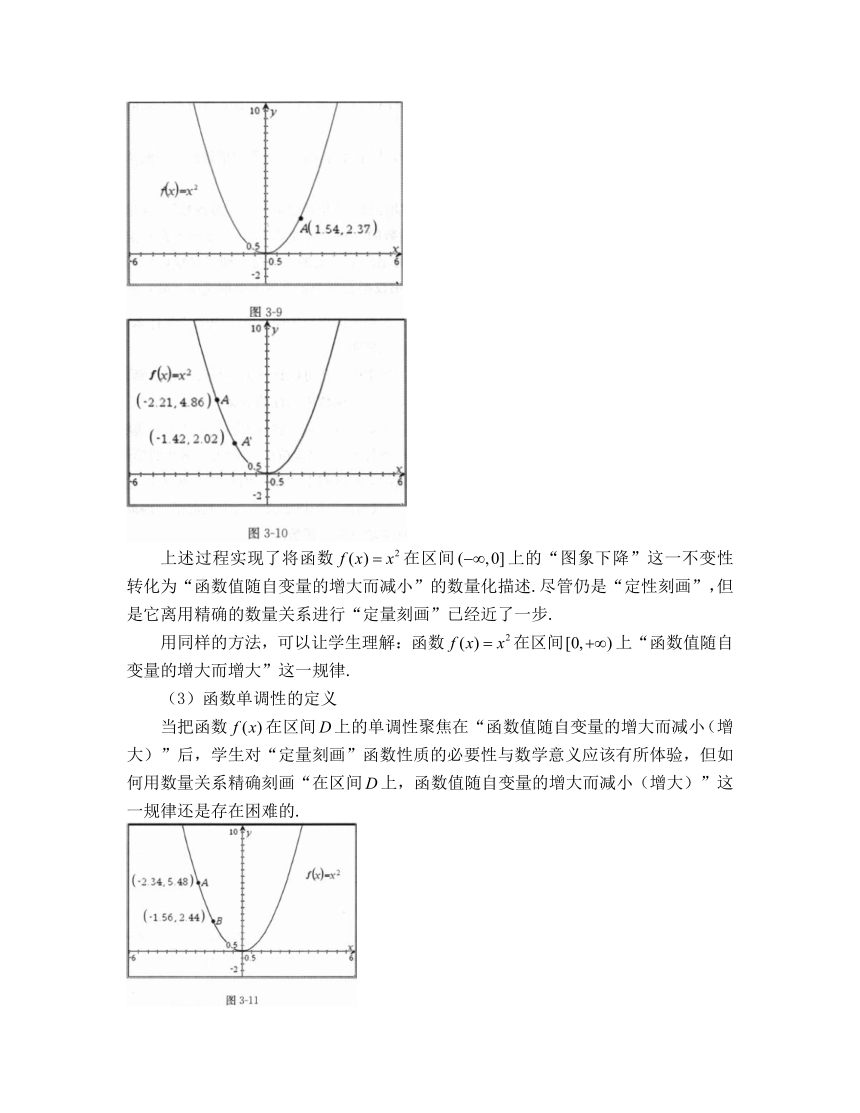
例如,对于教科书上的例子,可以借用信息技术给出图3-9,并提出问题:你能从函数的对应关系出发说出图中点的两个坐标的意义吗?
在学生回答后,可以在图3-9中轴的左侧沿增大的方向拖动点,让学生观察点的坐标变化(图3-10),引导他们得出函数值的变化规律:函数值随自变量的增大而减小.
上述过程实现了将函数在区间上的“图象下降”这一不变性转化为“函数值随自变量的增大而减小”的数量化描述.尽管仍是“定性刻画”,但是它离用精确的数量关系进行“定量刻画”已经近了一步.
用同样的方法,可以让学生理解:函数在区间上“函数值随自变量的增大而增大”这一规律.
(3)函数单调性的定义
当把函数在区间上的单调性聚焦在“函数值随自变量的增大而减小(增大)”后,学生对“定量刻画”函数性质的必要性与数学意义应该有所体验,但如何用数量关系精确刻画“在区间上,函数值随自变量的增大而减小(增大)”这一规律还是存在困难的.
对于函数而言,为进一步精确刻画它在区间上“函数值随自变量的增大而减小”这一规律,可以借助信息技术作出图3-11加以理解.在轴左侧任意改变,的位置,可以发现:只要保持点的横坐标大于点的横坐标,就会有点的纵坐标大于点的纵坐标.
利用函数的定义及解析式把上述规律表示出来,就可以得到函数在区间上满足:若,,且,就有.
虽然上述改变,的位置是随意的,但仍不能保证发现的结论在区间上的任何情况下都是正确的.因此,我们必须找到一种方法加以证明.这样,就有了以下用符号语言刻画的过程:
,,得到,,那么当时,
有.这时我们就说函数在上是单调递减的.
教科书的边空中要求学生说明“为什么”,实际上是让学生利用不等式的基本性质证明.
教学中,还可以让学生再举几个自己熟悉的例子,用上述方法描述函数的单调性.在此基础上,再引入函数单调性的定义.
需要注意的是,教科书区分了“单调递增”与“增函数”“单调递减”与“减函数”,这是与以往教科书有所不同的.实际上,函数的单调性是函数的一种“局部性质”,一个函数在其定义域内的某些区间上“增”而在另一些区间上“减”的情况是常见的.这时,如果仅仅以“增函数”“减函数”加以定义,会引起混淆.因此,教科书仅把在整个定义域上单调递增(减)的函数称为增(减)函数.
教科书给出函数单调性定义后设置了“思考”,意在引导学生体会函数的单调性是对定义域内的某个区间而言的.函数在某个区间上单调,并不意味着函数在整个定义域内都是单调的,教学时可以要求学生举例说明.
(4)函数的单调区间
在本节中,只需会求一次函数、二次函数、反比例函数及形如的简单函数的单调区间,而求更加复杂的函数的单调区间,待今后再学习.例如学习导数后,利用导数去求函数的单调区间.
在教学中,既要重视由函数图象获得单调区间,也应重视由函数的单调性帮助画函数的图象.这样数形结合地思考和解决问题,不仅可以更方便地发现解决问题的途径,而且有利于培养学生的直观想象素养.
(5)关于函数单调性的判定
虽然我们可以通过函数的图象了解函数的单调性,但证明函数在某个区间上单调递增(减),就必须回到定义上来.
从函数单调性定义可知,证明函数在某个区间上的单调性,需要用到不等式的性质和代数变形等.初中阶段,学生接触代数证明题较少,而通过代数运算(变形)证明数学命题是高中数学学习的重要任务,所以教学中应引起足够的重视.
让学生证明一些简单函数在某个区间上的单调性,不仅可以加深他们对函数单调性的理解,还可以让他们从中体会到面对“无穷”时的数学处理方法,从中感受数学的美与力量.
为了帮助学生规范证明过程,可以将(用定义)证明函数在区间上的单调性的过程归纳为以下步骤:
第一步,在区间上任取两个自变量的值,,并规定;
第二步,计算,将分解为若干可以直接确定符号的式子;
第三步,确定的符号.若,则函数在区间上单调递增;若,则函数在区间上单调递减.
(6)增(减)函数定义的等价形式
教科书习题3.2中的第9题,实际上是给出增(减)函数定义的等价形式.这个等价形式不仅可以简化判断单调性的过程,也为将来研究平均变化率与导数提供了基础,教学时要提醒学生加以注意.
比如,对于教科书上的例1,可以利用第9题中函数增减性的等价形式加以解决:,,且,则
.
当时,,所以是增函数;
当时,,所以是减函数.
(7)函数的单调区间不能简单合并
例如,函数在区间和上都单调递减,我们说函数在区间和上单调递减,但不能说在上单调递减,或在整个定义域内单调递减,即不能说是减函数.
(8)例题、练习与习题的处理
教科书在函数单调性部分安排了3个例题.
例1是利用单调性的定义研究一次函数的单调性.这里不仅是让学生熟悉利用定义研究函数单调性的过程,也是对初中阶段从图象中得到的结论进行严格的证明.此外,这里将“比较与的大小”转化为“比较与0的大小”的做法,体现了数学中“化繁为简”“化难为易”的转化与化归思想.
例2本质上是研究反比例函数的单调性.在用定义证明函数的单调性时,要特别注意培养学生数学表达的严谨性和书写过程的规范性.
例3中的函数其实是正比例函数与反比例函数的和.教学时,除按函数单调性的定义进行证明外,还可以引导学生用定义探究在整个定义域内的单调性.
如果利用习题3.2第9题所提供的单调性定义的等价形式,可以得到
.
因此,,,且,可以得到如下表格:
的符号
单调递增 单调递减 单调递减 单调递增
所以,的增区间是和,减区间是和.
本小节的4个练习可这样处理:第1题结合单调性定义进行处理;第2题结合例1处理;第3题、第4题结合例2进行处理.所有的练习应让学生独立思考后画出函数图象,以帮助理解问题中函数的单调性和证明过程.
2.函数的最大(小)值
函数的最大(小)值与函数的单调性有着密切的联系.通常,知道了函数的单调性,就能较方便地找到函数的最大(小)值.
(1)函数的最大(小)值的定义
函数的最大(小)值的定义是借助二次函数及其图象引出的,概念的出现仍然是遵循从特殊到一般的原则.这里给出了两个“思考”,第一个思考以学生熟悉的素材给学生提供尝试的机会,也为引出最大值概念作准备;第二个思考,是让学生学会用类比的方法独立获得最小值概念.教学时不要由教师取而代之,要给学生提升数学思维能力的机会,并结合具体实例解决函数最小值的理解问题.
(2)例题、练习与习题的处理
例4是一个实际应用问题,这里需要物理中的斜抛运动知识作准备,如果学生没有这方面的知识,那么教学时宜作适当的说明.
例5是借助函数的单调性求函数最值的问题.教学时,需要强调证明函数单调性的重要性,只有在证明了函数在给定区间上是单调递减的,才能说明函数在区间端点取到的函数值是函数的最大(小)值.
本小节的3个练习可这样处理:第1题配合例4;第2题配合最大(小)值的概念;第3题配合例5。
3.2.2奇偶性
与函数单调性不同,函数的奇偶性是函数的整体性质,即它要求定义域中任意一个自变量都具有这样的特性.
教科书在处理函数的奇偶性时,沿用了处理函数的单调性的方法,即先给出几个特殊函数的图象,让学生获得函数奇偶性的直观定性认识;然后利用表格研究发现数量变化特征;最后通过代数运算,验证发现的数量特征的普遍性,在此基础上建立奇(偶)函数概念.
将上述研究函数奇偶性的过程概括起来就是:
具体函数—图象特征(对称性)—数量刻画—符号语言—抽象定义—奇偶性判定.
1.偶函数
(1)偶函数的定性认识
教科书先研究偶函数.在引导学生观察函数和的图象时,发现图象关于轴对称应该是不难的,难的是如何精确刻画一个图象关于对称,所以教科书以“探究”的形式提出了问题.
教学时,不要一步到位地用符号语言刻画函数图象关于轴的对称,要为培养学生的数形结合思想创造机会.具体地,要让学生将现在的研究与函数单调性的研究联系起来,产生将自己发现的图象特征进行“定量刻画”的想法,进而寻找“定量刻画”的方法.
(2)偶函数的数量刻画
让学生观察下列表格中的数量特征:
··· -3 -2 -1 0 1 2 3 ···
··· 9 4 1 0 1 4 9 ···
··· -1 0 1 2 1 0 -1 ···
学生应该不难发现结论:自变量取一对相反数时,相应的两个函数值相等.
但是,“如何给定表格中自变量的取值”“上述发现的结论是否具有一般性”“如何说明上述结论具有一般性”是教学中应充分重视的问题.对于初学用符号语言刻画函数特征的学生来说,它们不仅是重点也是难点,教学时可以通过让学生回顾刻画函数单调性的方法来突破这个难点.
实际上,函数的奇偶性就是平面几何中中心对称图形、轴对称图形的解析表示.利用平面几何中轴对称的知识,对直角坐标系中点的位置关系与相应的坐标之间的关系稍作思考,就可以容易地想到:,点与点关于轴对称,那么轴是线段PP'的垂直平分线,根据坐标的意义即得;反之也对.
(3)偶函数的定义
教学时可以引导学生思考:
为何要从,,得出?
如何说明,都有?
这样做体现了从特殊到一般的思想,这是人们发现规律和不变性的重要方法,也是抽象数学概念的重要过程,教学时应注意给学生创造这样思考的机会.
对于上述第二个问题,教科书给出的处理过程如下:
实际上,,都有,这时称函数为偶函数.
在这里,要向学生说明用解析式证明第二个问题中的结论,实质上就是用符号语言刻画函数的性质.
教科书给出偶函数的定义与以往教科书给出的定义有所不同,在于强调了“偶函数的定义域关于原点对称”,即“如果,都有”,这在原来教科书定义中是一个隐性条件,现在将其显性化了.
2.奇函数
在给出偶函数定义的基础上,教科书设置了探究栏目,启发学生用类比的方法得出奇函数的定义.
为此,教科书在表3.2-2中留下大部分空格,旨在让学生自己动手计算填写数据,仿照偶函数概念建立的过程,独立地去经历发现、猜想与证明的全过程,并由此建立奇函数的概念.教学时要贯彻教科书的这一编写意图,放手让学生展开自主探究活动.
在得到奇函数的定义后,要让学生将奇函数的定义与偶函数的定义进行比较,指出奇函数与偶函数的共同点是:
(1)定义域关于原点对称;
(2)都是函数的整体性质.
奇函数与偶函数的不同点是:
(1)当自变量取一对相反数时,偶函数的函数值相等,而奇函数的函数值是一对相反数;
2)偶函数的图象关于轴对称,而奇函数的图象关于原点对称.
3.函数奇偶性的判定
根据奇(偶)函数的定义判断一个函数的奇偶性,可以按如下步骤进行:
第一步,求出函数的定义域.
第二步,判断定义域是否关于原点对称.若否,则函数不具有奇偶性,结束判断;若是,则进行第三步.
第三步,(为定义域),计算,若,则为偶函数;若,则为奇函数;若,且,则既不是偶函数也不是奇函数.
(1)注意在函数奇偶性判断中加强数形结合
有了偶函数的概念后,教科书给出了两个函数,加以说明.教学时,不仅要引导学生从偶函数的定义去思考,还要让他们想象一下这两个函数的图象.有条件的话,可让学生用信息技术画一画函数的图象.
对于一个奇函数或偶函数,根据它的图象关于原点或轴对称的特性,就可由自变量取正值时的图象和性质,来推断它在整个定义域内的图象和性质.其实,这也是研究函数奇偶性的好处所在——简化对函数的认识过程.
(2)奇(偶)函数定义的等价形式
设函数的定义域为,则有
是偶函数,,且;
是奇函数,,且.
以上形式在判断函数的奇偶性中非常有用,这种形式使得判断的方向很明确.
4.例题、练习与习题的处理
(1)教科书第85页上的“思考”,意在让学生通过函数的奇偶性画函数的图象.教学时,可将练习的第1题与之配合.
(2)例6的教学可与练习的第2题结合,目的是让学生用奇偶性的定义判断函数的奇偶性.
(3)应让学生认识到并不是所有的函数都具有奇偶性,如函数与既不是奇函数也不是偶函数,这可以从图象上让学生认识,也可以由定义去说明.因为它们的定义域分别是与,不关于原点对称,所以不满足奇函数与偶函数的定义.
(4)教科书在习题3.2中安排了函数的单调性与奇偶性相结合的问题,这是学生学习时的一个难点,教学时可适当增加这方面的题目.例如:
已知奇函数在上单调递增,证明在上也单调递增.
证明时,可按如下的步骤进行:
①把要证明的结论具体化.任取,,即,,且设,要证明.
②为利用在上所具有的性质,转而考虑,的相反数,,易知
,,且,
因为在上单调递增,所以
.
③根据是奇函数的条件,有,,所以,由上面的式子可知,即证得在上单调递增.
一、本节知识结构框图
二、重点、难点
重点:函数的单调性、奇偶性.
难点:增(减)函数的定义,利用增(减)函数的定义判断函数的单调性.
三、教科书编写意图及教学建议
运动变化的规律性是性质,变化中的不变性也是性质,函数是刻画客观世界中运动变化的重要数学模型,因此,运动变化中的规律性或不变性通常反映为函数的性质.
高中阶段要研究的函数性质有:单调性、最大(小)值、奇偶性、周期性、函数的零点、正或负增长率(衰减率)、增长(减少)快慢等.本节研究函数的单调性、最大(小)值、奇偶性,其中单调性是函数最重要的性质.
函数的单调性和奇偶性都可以在函数的图象上反映出来.因此,首先借助函数图象对其单调性和奇偶性有一个初步了解,并在此基础上进行定量刻画;然后用数学符号语言形成单调性与奇偶性的定义.这是研究函数性质的一般过程与方法,这样做有利于发展学生的数形结合思想,并由此培养学生数学抽象与直观想象等素养.
在教学时建议从若干实例出发,归纳出共同特征,再概括到同类事物中形成一般性质.这种从特殊到一般的归纳概括过程,有利于培养学生的数学思维和推理论证能力.
3.2.1单调性与最大(小)值
1.函数的单调性
学习函数的单调性,不仅可以让学生加深对函数基本性质的认识,而且可以让学生体会研究函数性质的过程与方法.
教科书给出研究函数单调性的过程是:
具体函数—图象特征—数量刻画—符号语言—抽象定义—单调性判定.
(1)函数单调性的定性刻画
教科书在研究函数的性质之前,给出了以下三个图形.
教学时可以让学生将图3-6与图3-7(或图3-8)进行比较,引导学生得出图3-6的特点是:图象从左至右保持上升;图3-7与图3-8的特点是:图象从左至右有升也有降.
由此产生问题:图3-6对应的函数图象“从左至右始终保持上升”,这一不变性是函数的什么性质呢?这里要注意在“如何观察”上加强启发和引导,学生在初中学过函数的单调性,采用描述“随的增大而增大(减小)”,这是从图象上看到的函数的变化趋势(变化中的不变性),所以学生借助初中的经验还是能够说出这种规律的.
对于图3-7与图3-8,观察发现,这两个函数图象具有的共同点是“在某个区间函数图象保持上升(或下降)”.因此,图3-6的函数图象从左到右始终保持上升,或者图3-7、图3-8的函数图象在某个区间保持上升(或下降),这是函数的一种性质,我们把这种性质归为函数的单调性.
(2)函数单调性的定量刻画
从图象观察到的函数单调性是“定性”的,需要进一步地用“定量”的方法对这一性质准确刻画,这就需要回到函数定义,利用函数符号.
例如,对于教科书上的例子,可以借用信息技术给出图3-9,并提出问题:你能从函数的对应关系出发说出图中点的两个坐标的意义吗?
在学生回答后,可以在图3-9中轴的左侧沿增大的方向拖动点,让学生观察点的坐标变化(图3-10),引导他们得出函数值的变化规律:函数值随自变量的增大而减小.
上述过程实现了将函数在区间上的“图象下降”这一不变性转化为“函数值随自变量的增大而减小”的数量化描述.尽管仍是“定性刻画”,但是它离用精确的数量关系进行“定量刻画”已经近了一步.
用同样的方法,可以让学生理解:函数在区间上“函数值随自变量的增大而增大”这一规律.
(3)函数单调性的定义
当把函数在区间上的单调性聚焦在“函数值随自变量的增大而减小(增大)”后,学生对“定量刻画”函数性质的必要性与数学意义应该有所体验,但如何用数量关系精确刻画“在区间上,函数值随自变量的增大而减小(增大)”这一规律还是存在困难的.
对于函数而言,为进一步精确刻画它在区间上“函数值随自变量的增大而减小”这一规律,可以借助信息技术作出图3-11加以理解.在轴左侧任意改变,的位置,可以发现:只要保持点的横坐标大于点的横坐标,就会有点的纵坐标大于点的纵坐标.
利用函数的定义及解析式把上述规律表示出来,就可以得到函数在区间上满足:若,,且,就有.
虽然上述改变,的位置是随意的,但仍不能保证发现的结论在区间上的任何情况下都是正确的.因此,我们必须找到一种方法加以证明.这样,就有了以下用符号语言刻画的过程:
,,得到,,那么当时,
有.这时我们就说函数在上是单调递减的.
教科书的边空中要求学生说明“为什么”,实际上是让学生利用不等式的基本性质证明.
教学中,还可以让学生再举几个自己熟悉的例子,用上述方法描述函数的单调性.在此基础上,再引入函数单调性的定义.
需要注意的是,教科书区分了“单调递增”与“增函数”“单调递减”与“减函数”,这是与以往教科书有所不同的.实际上,函数的单调性是函数的一种“局部性质”,一个函数在其定义域内的某些区间上“增”而在另一些区间上“减”的情况是常见的.这时,如果仅仅以“增函数”“减函数”加以定义,会引起混淆.因此,教科书仅把在整个定义域上单调递增(减)的函数称为增(减)函数.
教科书给出函数单调性定义后设置了“思考”,意在引导学生体会函数的单调性是对定义域内的某个区间而言的.函数在某个区间上单调,并不意味着函数在整个定义域内都是单调的,教学时可以要求学生举例说明.
(4)函数的单调区间
在本节中,只需会求一次函数、二次函数、反比例函数及形如的简单函数的单调区间,而求更加复杂的函数的单调区间,待今后再学习.例如学习导数后,利用导数去求函数的单调区间.
在教学中,既要重视由函数图象获得单调区间,也应重视由函数的单调性帮助画函数的图象.这样数形结合地思考和解决问题,不仅可以更方便地发现解决问题的途径,而且有利于培养学生的直观想象素养.
(5)关于函数单调性的判定
虽然我们可以通过函数的图象了解函数的单调性,但证明函数在某个区间上单调递增(减),就必须回到定义上来.
从函数单调性定义可知,证明函数在某个区间上的单调性,需要用到不等式的性质和代数变形等.初中阶段,学生接触代数证明题较少,而通过代数运算(变形)证明数学命题是高中数学学习的重要任务,所以教学中应引起足够的重视.
让学生证明一些简单函数在某个区间上的单调性,不仅可以加深他们对函数单调性的理解,还可以让他们从中体会到面对“无穷”时的数学处理方法,从中感受数学的美与力量.
为了帮助学生规范证明过程,可以将(用定义)证明函数在区间上的单调性的过程归纳为以下步骤:
第一步,在区间上任取两个自变量的值,,并规定;
第二步,计算,将分解为若干可以直接确定符号的式子;
第三步,确定的符号.若,则函数在区间上单调递增;若,则函数在区间上单调递减.
(6)增(减)函数定义的等价形式
教科书习题3.2中的第9题,实际上是给出增(减)函数定义的等价形式.这个等价形式不仅可以简化判断单调性的过程,也为将来研究平均变化率与导数提供了基础,教学时要提醒学生加以注意.
比如,对于教科书上的例1,可以利用第9题中函数增减性的等价形式加以解决:,,且,则
.
当时,,所以是增函数;
当时,,所以是减函数.
(7)函数的单调区间不能简单合并
例如,函数在区间和上都单调递减,我们说函数在区间和上单调递减,但不能说在上单调递减,或在整个定义域内单调递减,即不能说是减函数.
(8)例题、练习与习题的处理
教科书在函数单调性部分安排了3个例题.
例1是利用单调性的定义研究一次函数的单调性.这里不仅是让学生熟悉利用定义研究函数单调性的过程,也是对初中阶段从图象中得到的结论进行严格的证明.此外,这里将“比较与的大小”转化为“比较与0的大小”的做法,体现了数学中“化繁为简”“化难为易”的转化与化归思想.
例2本质上是研究反比例函数的单调性.在用定义证明函数的单调性时,要特别注意培养学生数学表达的严谨性和书写过程的规范性.
例3中的函数其实是正比例函数与反比例函数的和.教学时,除按函数单调性的定义进行证明外,还可以引导学生用定义探究在整个定义域内的单调性.
如果利用习题3.2第9题所提供的单调性定义的等价形式,可以得到
.
因此,,,且,可以得到如下表格:
的符号
单调递增 单调递减 单调递减 单调递增
所以,的增区间是和,减区间是和.
本小节的4个练习可这样处理:第1题结合单调性定义进行处理;第2题结合例1处理;第3题、第4题结合例2进行处理.所有的练习应让学生独立思考后画出函数图象,以帮助理解问题中函数的单调性和证明过程.
2.函数的最大(小)值
函数的最大(小)值与函数的单调性有着密切的联系.通常,知道了函数的单调性,就能较方便地找到函数的最大(小)值.
(1)函数的最大(小)值的定义
函数的最大(小)值的定义是借助二次函数及其图象引出的,概念的出现仍然是遵循从特殊到一般的原则.这里给出了两个“思考”,第一个思考以学生熟悉的素材给学生提供尝试的机会,也为引出最大值概念作准备;第二个思考,是让学生学会用类比的方法独立获得最小值概念.教学时不要由教师取而代之,要给学生提升数学思维能力的机会,并结合具体实例解决函数最小值的理解问题.
(2)例题、练习与习题的处理
例4是一个实际应用问题,这里需要物理中的斜抛运动知识作准备,如果学生没有这方面的知识,那么教学时宜作适当的说明.
例5是借助函数的单调性求函数最值的问题.教学时,需要强调证明函数单调性的重要性,只有在证明了函数在给定区间上是单调递减的,才能说明函数在区间端点取到的函数值是函数的最大(小)值.
本小节的3个练习可这样处理:第1题配合例4;第2题配合最大(小)值的概念;第3题配合例5。
3.2.2奇偶性
与函数单调性不同,函数的奇偶性是函数的整体性质,即它要求定义域中任意一个自变量都具有这样的特性.
教科书在处理函数的奇偶性时,沿用了处理函数的单调性的方法,即先给出几个特殊函数的图象,让学生获得函数奇偶性的直观定性认识;然后利用表格研究发现数量变化特征;最后通过代数运算,验证发现的数量特征的普遍性,在此基础上建立奇(偶)函数概念.
将上述研究函数奇偶性的过程概括起来就是:
具体函数—图象特征(对称性)—数量刻画—符号语言—抽象定义—奇偶性判定.
1.偶函数
(1)偶函数的定性认识
教科书先研究偶函数.在引导学生观察函数和的图象时,发现图象关于轴对称应该是不难的,难的是如何精确刻画一个图象关于对称,所以教科书以“探究”的形式提出了问题.
教学时,不要一步到位地用符号语言刻画函数图象关于轴的对称,要为培养学生的数形结合思想创造机会.具体地,要让学生将现在的研究与函数单调性的研究联系起来,产生将自己发现的图象特征进行“定量刻画”的想法,进而寻找“定量刻画”的方法.
(2)偶函数的数量刻画
让学生观察下列表格中的数量特征:
··· -3 -2 -1 0 1 2 3 ···
··· 9 4 1 0 1 4 9 ···
··· -1 0 1 2 1 0 -1 ···
学生应该不难发现结论:自变量取一对相反数时,相应的两个函数值相等.
但是,“如何给定表格中自变量的取值”“上述发现的结论是否具有一般性”“如何说明上述结论具有一般性”是教学中应充分重视的问题.对于初学用符号语言刻画函数特征的学生来说,它们不仅是重点也是难点,教学时可以通过让学生回顾刻画函数单调性的方法来突破这个难点.
实际上,函数的奇偶性就是平面几何中中心对称图形、轴对称图形的解析表示.利用平面几何中轴对称的知识,对直角坐标系中点的位置关系与相应的坐标之间的关系稍作思考,就可以容易地想到:,点与点关于轴对称,那么轴是线段PP'的垂直平分线,根据坐标的意义即得;反之也对.
(3)偶函数的定义
教学时可以引导学生思考:
为何要从,,得出?
如何说明,都有?
这样做体现了从特殊到一般的思想,这是人们发现规律和不变性的重要方法,也是抽象数学概念的重要过程,教学时应注意给学生创造这样思考的机会.
对于上述第二个问题,教科书给出的处理过程如下:
实际上,,都有,这时称函数为偶函数.
在这里,要向学生说明用解析式证明第二个问题中的结论,实质上就是用符号语言刻画函数的性质.
教科书给出偶函数的定义与以往教科书给出的定义有所不同,在于强调了“偶函数的定义域关于原点对称”,即“如果,都有”,这在原来教科书定义中是一个隐性条件,现在将其显性化了.
2.奇函数
在给出偶函数定义的基础上,教科书设置了探究栏目,启发学生用类比的方法得出奇函数的定义.
为此,教科书在表3.2-2中留下大部分空格,旨在让学生自己动手计算填写数据,仿照偶函数概念建立的过程,独立地去经历发现、猜想与证明的全过程,并由此建立奇函数的概念.教学时要贯彻教科书的这一编写意图,放手让学生展开自主探究活动.
在得到奇函数的定义后,要让学生将奇函数的定义与偶函数的定义进行比较,指出奇函数与偶函数的共同点是:
(1)定义域关于原点对称;
(2)都是函数的整体性质.
奇函数与偶函数的不同点是:
(1)当自变量取一对相反数时,偶函数的函数值相等,而奇函数的函数值是一对相反数;
2)偶函数的图象关于轴对称,而奇函数的图象关于原点对称.
3.函数奇偶性的判定
根据奇(偶)函数的定义判断一个函数的奇偶性,可以按如下步骤进行:
第一步,求出函数的定义域.
第二步,判断定义域是否关于原点对称.若否,则函数不具有奇偶性,结束判断;若是,则进行第三步.
第三步,(为定义域),计算,若,则为偶函数;若,则为奇函数;若,且,则既不是偶函数也不是奇函数.
(1)注意在函数奇偶性判断中加强数形结合
有了偶函数的概念后,教科书给出了两个函数,加以说明.教学时,不仅要引导学生从偶函数的定义去思考,还要让他们想象一下这两个函数的图象.有条件的话,可让学生用信息技术画一画函数的图象.
对于一个奇函数或偶函数,根据它的图象关于原点或轴对称的特性,就可由自变量取正值时的图象和性质,来推断它在整个定义域内的图象和性质.其实,这也是研究函数奇偶性的好处所在——简化对函数的认识过程.
(2)奇(偶)函数定义的等价形式
设函数的定义域为,则有
是偶函数,,且;
是奇函数,,且.
以上形式在判断函数的奇偶性中非常有用,这种形式使得判断的方向很明确.
4.例题、练习与习题的处理
(1)教科书第85页上的“思考”,意在让学生通过函数的奇偶性画函数的图象.教学时,可将练习的第1题与之配合.
(2)例6的教学可与练习的第2题结合,目的是让学生用奇偶性的定义判断函数的奇偶性.
(3)应让学生认识到并不是所有的函数都具有奇偶性,如函数与既不是奇函数也不是偶函数,这可以从图象上让学生认识,也可以由定义去说明.因为它们的定义域分别是与,不关于原点对称,所以不满足奇函数与偶函数的定义.
(4)教科书在习题3.2中安排了函数的单调性与奇偶性相结合的问题,这是学生学习时的一个难点,教学时可适当增加这方面的题目.例如:
已知奇函数在上单调递增,证明在上也单调递增.
证明时,可按如下的步骤进行:
①把要证明的结论具体化.任取,,即,,且设,要证明.
②为利用在上所具有的性质,转而考虑,的相反数,,易知
,,且,
因为在上单调递增,所以
.
③根据是奇函数的条件,有,,所以,由上面的式子可知,即证得在上单调递增.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
