平行四边形的性质(二)[下学期]
文档属性
| 名称 | 平行四边形的性质(二)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-31 00:00:00 | ||
图片预览



文档简介
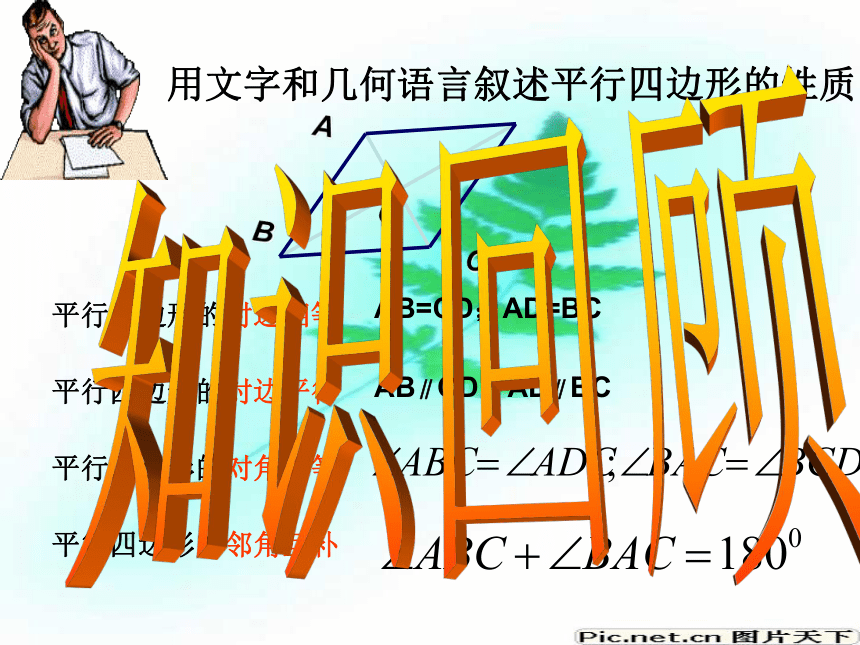
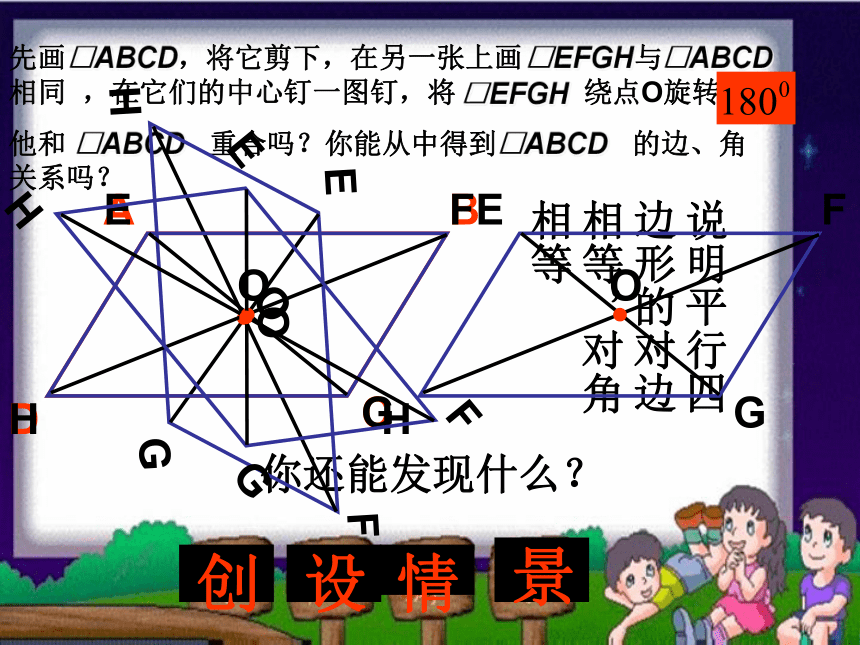
课件15张PPT。平行四边形的性质(二)用文字和几何语言叙述平行四边形的性质平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的邻角互补AB=CD;AD=BCAB∥CD;AD∥BC知识回顾创设情景你还能发现什么?说明平行四边形的对边相等,对角相等平行四边形的对角线互相平分平行四边形的又一个性质∵四边形ABCD是平行四边形∴OA=OC
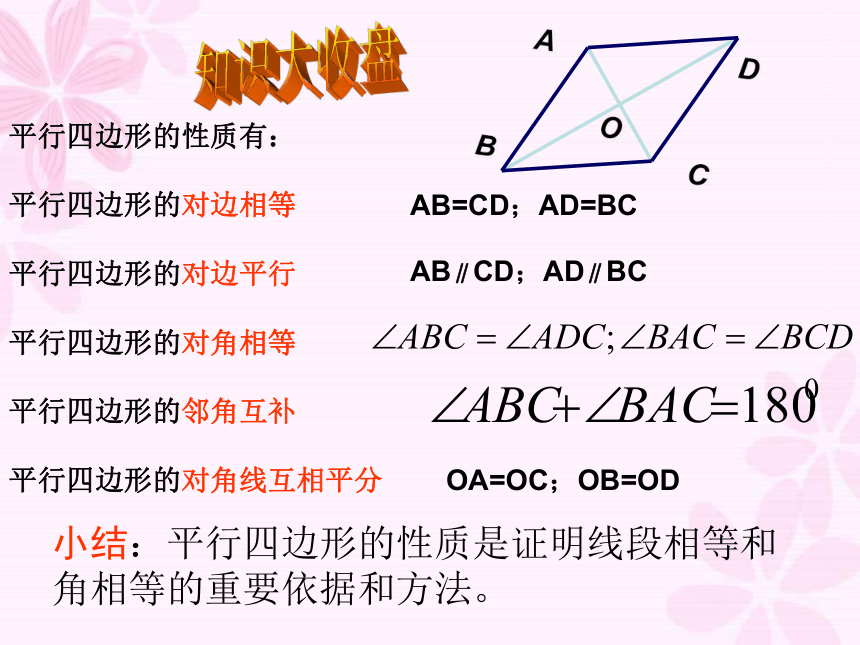
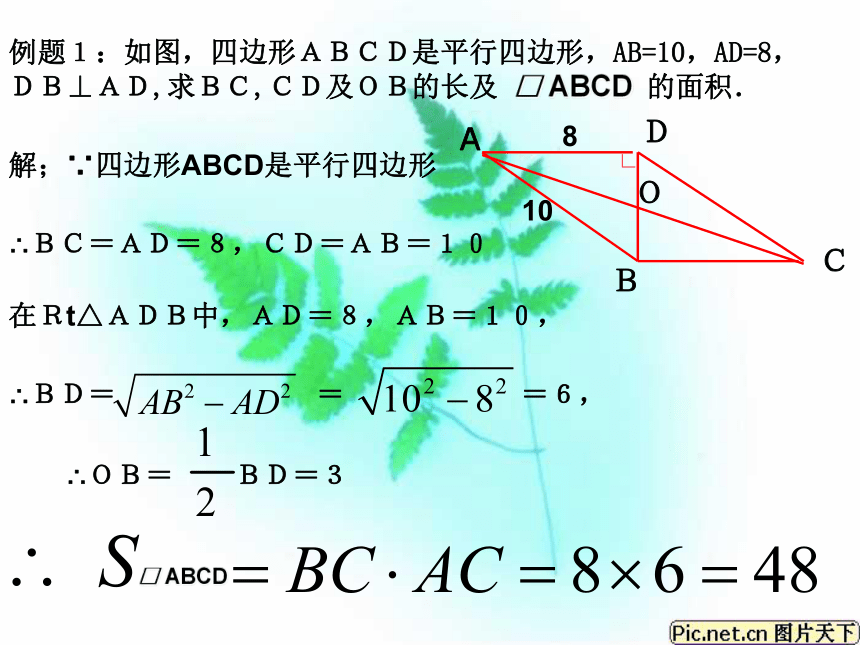
OB=OD知识大收盘平行四边形的性质有:平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的对角线互相平分平行四边形的邻角互补AB=CD;AD=BCAB∥CD;AD∥BCOA=OC;OB=OD小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。例题1:如图,四边形ABCD是平行四边形,AB=10,AD=8, DB⊥AD,求BC,CD及OB的长及 □ ABCD 的面积.解;∵四边形ABCD是平行四边形∴OB= BD=3∴BD= = =6,在Rt△ADB中,AD=8,AB=10,∴BC=AD=8,CD=AB=10□ ABCD解:∴△AOB是直角三角形∴△AOD是直角三角形如图 在?ABC中,AD平分∠BAC,点M,E,F分别 是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM∴ AF=BM∴ AF=EF∴∠CAD =∠AEF∴ ∠BAD=∠AEF∵AB//EF∴∠BAD=∠CAD∵ AD平分∠BAC∴BM=EF AB//EF证明: ∵ 四边形BEFM是平行四边形解:在□ ABCD中在△AOB中BO-AO<AB<AO+BO既1 <AB <11做一做,比一比 1.判断:
①平行四边形是轴对称图形 ( )
②平行四边形的边相等 ( )
③平行四边形的内角相等 ( )
④对边平行的四边形叫平行四边形 ( )2.选择:平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对边平行且相等
C、内角的为360度 D、外角和为360度╳╳╳╳B数一数,图中有 个平行四边形。 平行四边形不具有的性质有哪( )A、对边平行 B、对角互补
C、对边相等 D、对角线互相平分
E 、对角线互相垂直9B、E1、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
2、已知, ABCD的周长是28,对角线AC,BD相交于点O,且△OAB的周长比△OBC的周长大4,则AB=
3、已知P为 ABCD的边CD上的任意点,则S△APB与S ABCD的比为
4、如图:P是 ABCD内的
一点, ,则 =创新演练S△APBS△CPDAD91:2学过了本节课,你有哪些收获?1.平行四边形的定义、表示方法、对角线 2.平行四边形的性质:
平行四边形的对边平行且相等
平行四边形的 对角相等
平行四边形的 邻角互补
平行四边形的 对角线互相平分 3.可以用测量的方法,还可以用证明的方法来探索平行四边形的性质。回
味
无
穷2.如图:在 ABCD中,已知AC=3cm, ABC的周长为8cm,求平行四边形的周长4.如图在 ABCD中,E,F是对角线AC上的两点,且AE=CF.请你说明∠ ADF=∠CBE的理由
OB=OD知识大收盘平行四边形的性质有:平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的对角线互相平分平行四边形的邻角互补AB=CD;AD=BCAB∥CD;AD∥BCOA=OC;OB=OD小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。例题1:如图,四边形ABCD是平行四边形,AB=10,AD=8, DB⊥AD,求BC,CD及OB的长及 □ ABCD 的面积.解;∵四边形ABCD是平行四边形∴OB= BD=3∴BD= = =6,在Rt△ADB中,AD=8,AB=10,∴BC=AD=8,CD=AB=10□ ABCD解:∴△AOB是直角三角形∴△AOD是直角三角形如图 在?ABC中,AD平分∠BAC,点M,E,F分别 是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM∴ AF=BM∴ AF=EF∴∠CAD =∠AEF∴ ∠BAD=∠AEF∵AB//EF∴∠BAD=∠CAD∵ AD平分∠BAC∴BM=EF AB//EF证明: ∵ 四边形BEFM是平行四边形解:在□ ABCD中在△AOB中BO-AO<AB<AO+BO既1 <AB <11做一做,比一比 1.判断:
①平行四边形是轴对称图形 ( )
②平行四边形的边相等 ( )
③平行四边形的内角相等 ( )
④对边平行的四边形叫平行四边形 ( )2.选择:平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对边平行且相等
C、内角的为360度 D、外角和为360度╳╳╳╳B数一数,图中有 个平行四边形。 平行四边形不具有的性质有哪( )A、对边平行 B、对角互补
C、对边相等 D、对角线互相平分
E 、对角线互相垂直9B、E1、若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
2、已知, ABCD的周长是28,对角线AC,BD相交于点O,且△OAB的周长比△OBC的周长大4,则AB=
3、已知P为 ABCD的边CD上的任意点,则S△APB与S ABCD的比为
4、如图:P是 ABCD内的
一点, ,则 =创新演练S△APBS△CPDAD91:2学过了本节课,你有哪些收获?1.平行四边形的定义、表示方法、对角线 2.平行四边形的性质:
平行四边形的对边平行且相等
平行四边形的 对角相等
平行四边形的 邻角互补
平行四边形的 对角线互相平分 3.可以用测量的方法,还可以用证明的方法来探索平行四边形的性质。回
味
无
穷2.如图:在 ABCD中,已知AC=3cm, ABC的周长为8cm,求平行四边形的周长4.如图在 ABCD中,E,F是对角线AC上的两点,且AE=CF.请你说明∠ ADF=∠CBE的理由
