高中数学必修第一册人教A版(2019)《3.2函数的奇偶性》名师课件(共20张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版(2019)《3.2函数的奇偶性》名师课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 21:20:48 | ||
图片预览




文档简介
(共20张PPT)
人教A版同步教材名师课件
函数的奇偶性
学习目标
学 习 目 标 核心素养
通过具体实例加深对奇函数、偶函数定义的理解 数学抽象
掌握奇函数、偶函数的图象特征 直观想象
会判断和证明函数的奇偶性,注意定义域的影响 逻辑推理
学习目标
课程目标
1、理解函数的奇偶性及其几何意义;
2、学会运用函数图象理解和研究函数的性质;
3、学会判断函数的奇偶性.
数学学科素养
1.数学抽象:用数学语言表示函数奇偶性;
2.逻辑推理:证明函数奇偶性;
3.数学运算:运用函数奇偶性求参数;
4.数据分析:利用图象求奇偶函数;
5.数学建模:在具体问题情境中,运用数形结合思想,利用奇偶性解决实际问题.
探究新知
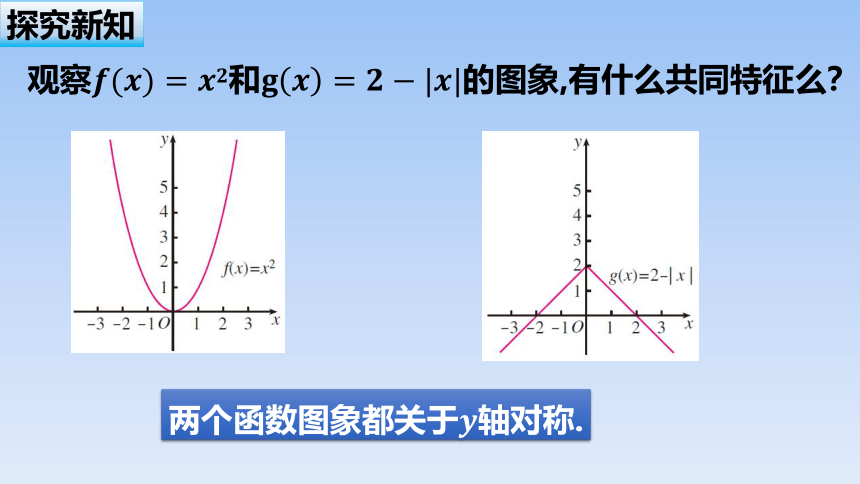
观察和的图象,有什么共同特征么?
两个函数图象都关于轴对称.
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x) … 16 9 4 1 0 1 4 9 16 …
… -2 -1 0 1 2 1 0 -1 -2 …
探究新知
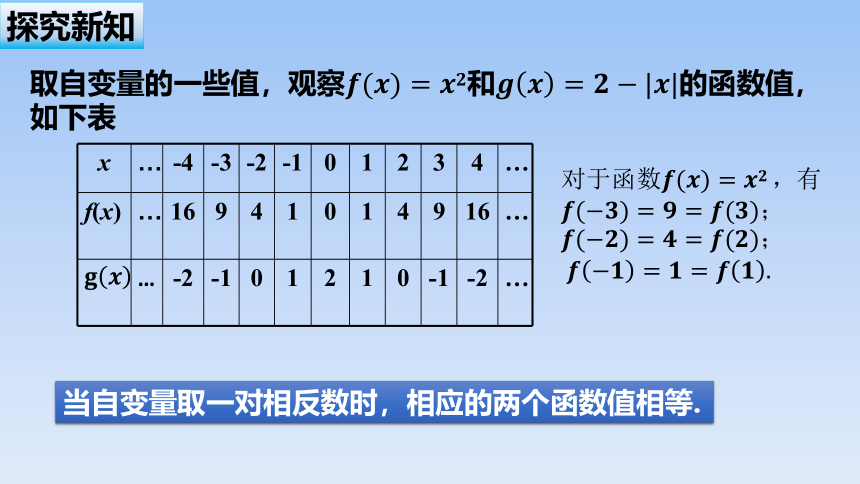
取自变量的一些值,观察和的函数值,
如下表
当自变量取一对相反数时,相应的两个函数值相等.
对于函数,有
;
探究新知
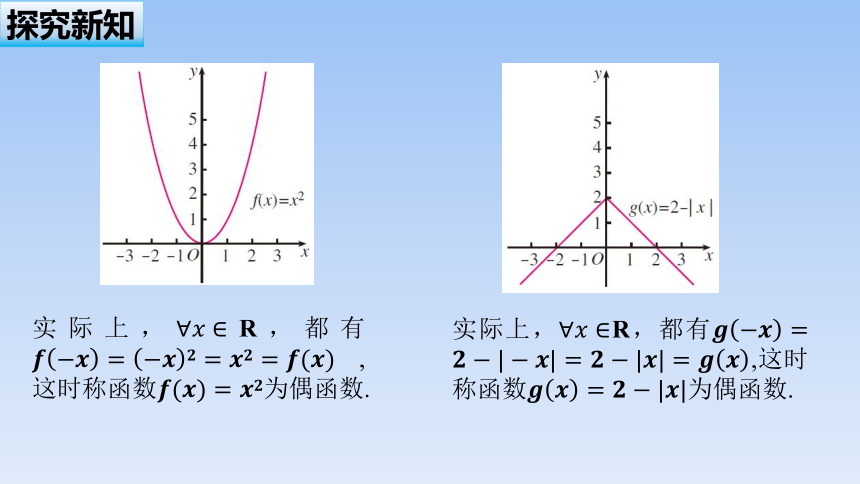
实际上,R,都有,这时称函数为偶函数.
实际上,R,都有,这时称函数为偶函数.
探究新知
一般地,设函数的定义域为,如果,都有,且那么函数就叫做偶函数(even function).
偶函数
探究新知
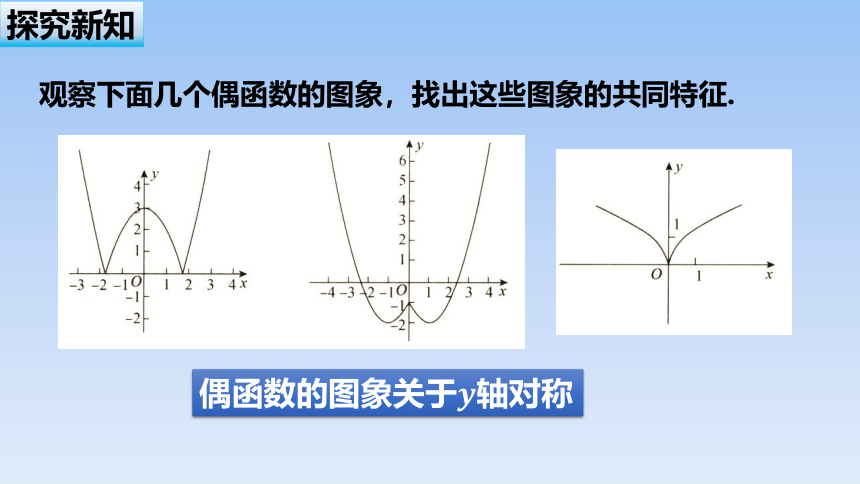
观察下面几个偶函数的图象,找出这些图象的共同特征.
偶函数的图象关于轴对称
探究新知
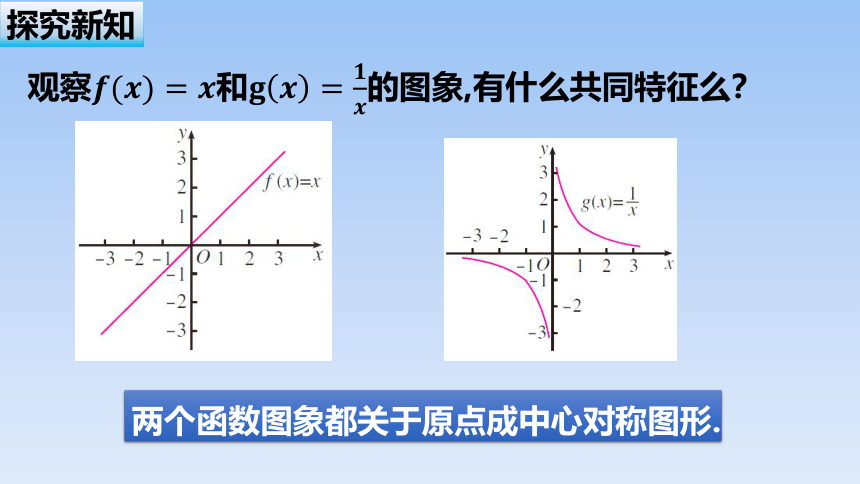
观察和的图象,有什么共同特征么?
两个函数图象都关于原点成中心对称图形.
探究新知
实际上,R,都有,这时称函数为奇函数.
实际上,R,都有,这时称函数为奇函数.
探究新知
一般地,设函数的定义域为,如果,都有,且那么函数就叫做奇函数(odd function).
奇函数
新知讲解
一般地,设函数的定义域为,如果,都有,且那么函数就叫做偶函数(even function).
偶函数
一般地,设函数的定义域为,如果,都有,且那么函数就叫做奇函数(odd function).
奇函数
定义域关于原点对称
如果函数是奇函数,则这个函数的图象是以坐标原点为对称中心的中心对称图形;若函数图象关于原点对称,则函数为奇函数.
如果函数是偶函数,则这个函数的图象是以y轴为对称轴的轴对称图形;若函数图象关于y轴对称,则函数为偶函数.
典例讲解
例1.判断下列函数的奇偶性:
.
解析
思路分析
本题考查利用奇偶性的定义判断函数的奇偶性.解题的关键是确定函数的定义域是否关于原点对称,然后化简函数解析式,验证与的关系.
(1)∵函数的定义域是,关于原点不对称,
∴既不是奇函数也不是偶函数.
(2) ∵函数的定义域是R,关于坐标原点对称.
又, ∴是偶函数.
(3)的定义域为,则.
∵ ∴是奇函数
用定义判断函数奇偶性的步骤:
求定义域
定义域
是否关于
原点对称
非奇非偶函数
看与的关系
若,
则为偶函数
若,则为奇函数
y
n
若且 , 则为既奇又偶函数
判断
若且 , 则为非奇非偶函数
1.判断下列函数的奇偶性.
变式训练
解析
;;
;.
(1)函数的定义域为,关于原点对称,对于定义域内的每一个都有,从而函数为奇函数.
(2)函数的定义域为R,关于原点对称,对于定义域内的每一个都有;从而函数为偶函数.
(3)函数的定义域为R,关于原点对称,由于,从而函数既不是奇函数也不是偶函数.
(4)的定义域为{2},不关于原点对称,∴函数既不是奇函数也不是偶函数.
例2.已知函数是R上的偶函数,在(- ,0]上的图像如图,你能试作出[0,+ )的图像吗?
y
x
0
典例讲解
偶函数满足的条件: 定义域关于原点对称
思路分析
解析
2.已知函数是R上的奇函数,在上的图像如图,作出的图像.
y
x
0
变式训练
解析
当堂检测
1.函数的图象 ( )
A.关于原点对称 B.关于直线对称
C.关于轴对称 D.关于轴对称
2.下列函数中既是偶函数,又在上单调递增的是 ( )
A. B. C. D.
3.函数是定义在R上的偶函数,当时,,则.
4.奇函数的定义域是,则.
A
C
-1
6
归纳小结
奇偶性
作 业
课本P85练习:1、2
人教A版同步教材名师课件
函数的奇偶性
学习目标
学 习 目 标 核心素养
通过具体实例加深对奇函数、偶函数定义的理解 数学抽象
掌握奇函数、偶函数的图象特征 直观想象
会判断和证明函数的奇偶性,注意定义域的影响 逻辑推理
学习目标
课程目标
1、理解函数的奇偶性及其几何意义;
2、学会运用函数图象理解和研究函数的性质;
3、学会判断函数的奇偶性.
数学学科素养
1.数学抽象:用数学语言表示函数奇偶性;
2.逻辑推理:证明函数奇偶性;
3.数学运算:运用函数奇偶性求参数;
4.数据分析:利用图象求奇偶函数;
5.数学建模:在具体问题情境中,运用数形结合思想,利用奇偶性解决实际问题.
探究新知
观察和的图象,有什么共同特征么?
两个函数图象都关于轴对称.
x … -4 -3 -2 -1 0 1 2 3 4 …
f(x) … 16 9 4 1 0 1 4 9 16 …
… -2 -1 0 1 2 1 0 -1 -2 …
探究新知
取自变量的一些值,观察和的函数值,
如下表
当自变量取一对相反数时,相应的两个函数值相等.
对于函数,有
;
探究新知
实际上,R,都有,这时称函数为偶函数.
实际上,R,都有,这时称函数为偶函数.
探究新知
一般地,设函数的定义域为,如果,都有,且那么函数就叫做偶函数(even function).
偶函数
探究新知
观察下面几个偶函数的图象,找出这些图象的共同特征.
偶函数的图象关于轴对称
探究新知
观察和的图象,有什么共同特征么?
两个函数图象都关于原点成中心对称图形.
探究新知
实际上,R,都有,这时称函数为奇函数.
实际上,R,都有,这时称函数为奇函数.
探究新知
一般地,设函数的定义域为,如果,都有,且那么函数就叫做奇函数(odd function).
奇函数
新知讲解
一般地,设函数的定义域为,如果,都有,且那么函数就叫做偶函数(even function).
偶函数
一般地,设函数的定义域为,如果,都有,且那么函数就叫做奇函数(odd function).
奇函数
定义域关于原点对称
如果函数是奇函数,则这个函数的图象是以坐标原点为对称中心的中心对称图形;若函数图象关于原点对称,则函数为奇函数.
如果函数是偶函数,则这个函数的图象是以y轴为对称轴的轴对称图形;若函数图象关于y轴对称,则函数为偶函数.
典例讲解
例1.判断下列函数的奇偶性:
.
解析
思路分析
本题考查利用奇偶性的定义判断函数的奇偶性.解题的关键是确定函数的定义域是否关于原点对称,然后化简函数解析式,验证与的关系.
(1)∵函数的定义域是,关于原点不对称,
∴既不是奇函数也不是偶函数.
(2) ∵函数的定义域是R,关于坐标原点对称.
又, ∴是偶函数.
(3)的定义域为,则.
∵ ∴是奇函数
用定义判断函数奇偶性的步骤:
求定义域
定义域
是否关于
原点对称
非奇非偶函数
看与的关系
若,
则为偶函数
若,则为奇函数
y
n
若且 , 则为既奇又偶函数
判断
若且 , 则为非奇非偶函数
1.判断下列函数的奇偶性.
变式训练
解析
;;
;.
(1)函数的定义域为,关于原点对称,对于定义域内的每一个都有,从而函数为奇函数.
(2)函数的定义域为R,关于原点对称,对于定义域内的每一个都有;从而函数为偶函数.
(3)函数的定义域为R,关于原点对称,由于,从而函数既不是奇函数也不是偶函数.
(4)的定义域为{2},不关于原点对称,∴函数既不是奇函数也不是偶函数.
例2.已知函数是R上的偶函数,在(- ,0]上的图像如图,你能试作出[0,+ )的图像吗?
y
x
0
典例讲解
偶函数满足的条件: 定义域关于原点对称
思路分析
解析
2.已知函数是R上的奇函数,在上的图像如图,作出的图像.
y
x
0
变式训练
解析
当堂检测
1.函数的图象 ( )
A.关于原点对称 B.关于直线对称
C.关于轴对称 D.关于轴对称
2.下列函数中既是偶函数,又在上单调递增的是 ( )
A. B. C. D.
3.函数是定义在R上的偶函数,当时,,则.
4.奇函数的定义域是,则.
A
C
-1
6
归纳小结
奇偶性
作 业
课本P85练习:1、2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
