19.1平行四边形性质(2)[下学期]
文档属性
| 名称 | 19.1平行四边形性质(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-02 10:03:00 | ||
图片预览



文档简介
课件20张PPT。19.1.1平行四边形的性质(2)◆什么是平行四边形?
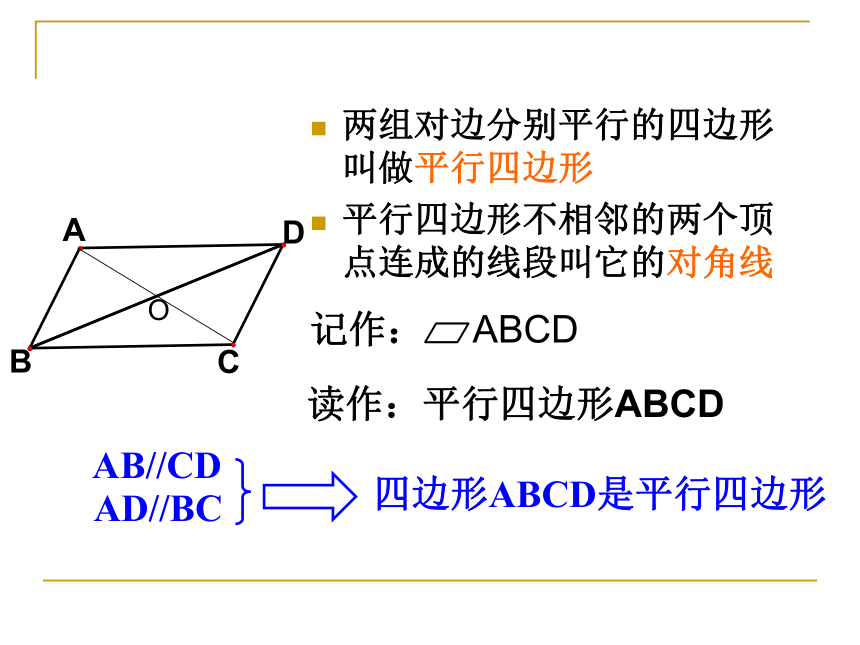
◆ 上节课我们掌握了平行四边形的哪些性质?复习回顾:两组对边分别平行的四边形叫做平行四边形
平行四边形不相邻的两个顶点连成的线段叫它的对角线记作: ABCD 读作:平行四边形ABCDOAB//CDAD//BC四边形ABCD是平行四边形平行四边形的性质观察平行四边形的四条边及其四个内角,你能发现哪些结论?
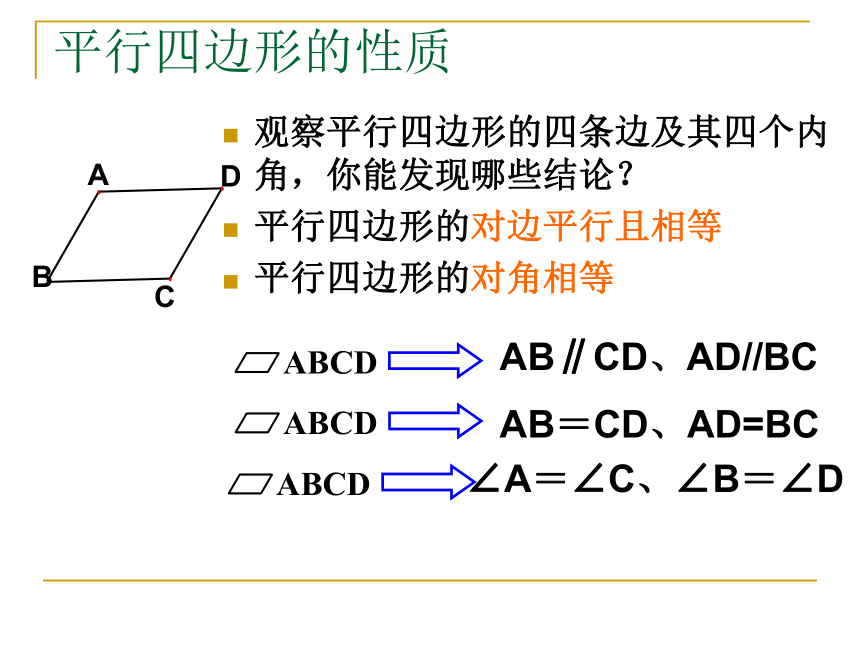
平行四边形的对边平行且相等
平行四边形的对角相等ABCD AB∥CD、AD//BCABCD AB=CD、AD=BCABCD ∠A=∠C、∠B=∠D
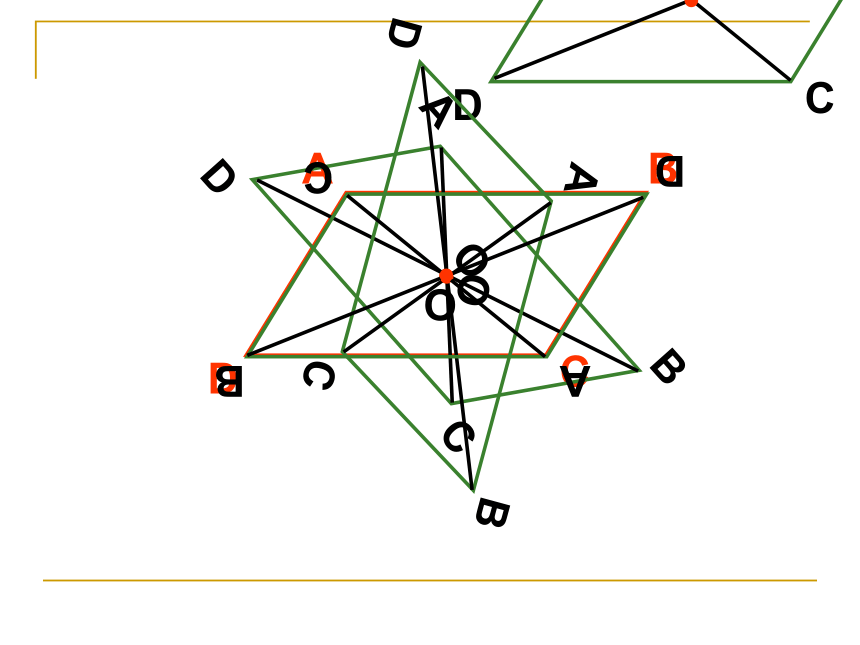
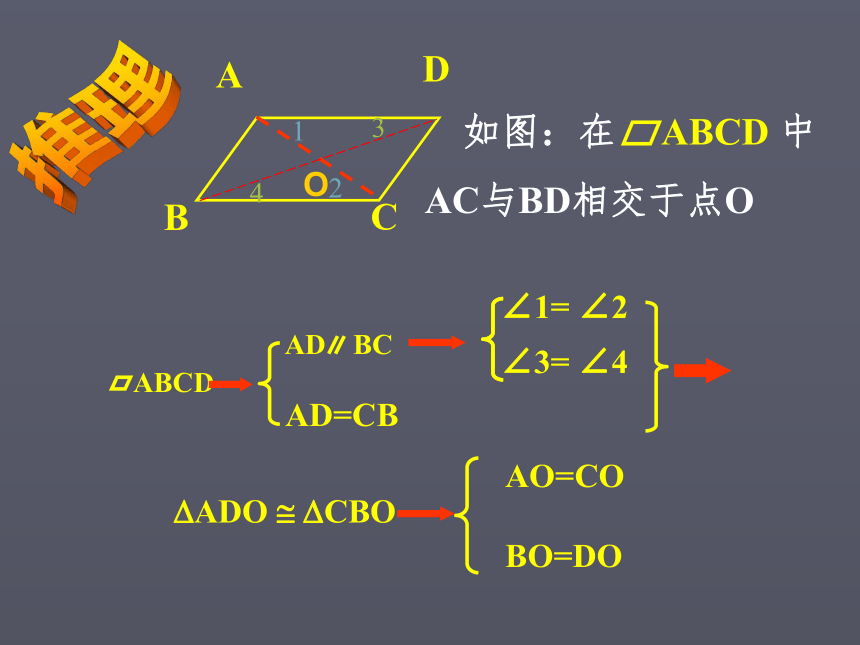
探究2:在纸上画□ABCD,将它剪下.再在一张纸上沿□ABCD的边缘画出一个与□ABCD相同的□EFGH.在它们的中心O(两条对角线的交点)钉一个图钉.将□ABCD绕点O旋转180°,它还和□EFGH重合吗?你能从中看出前面得到的□ABCD的边角关系吗?
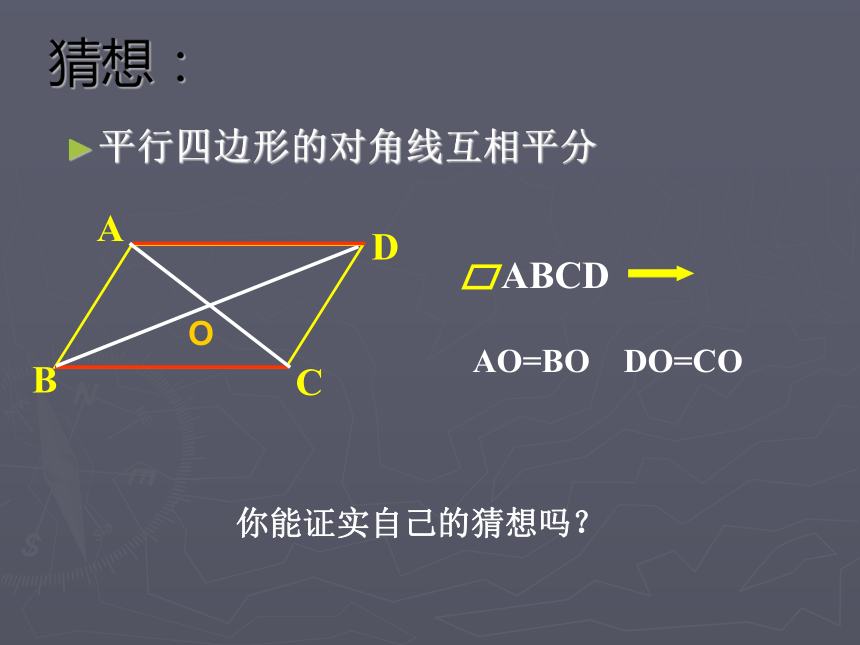
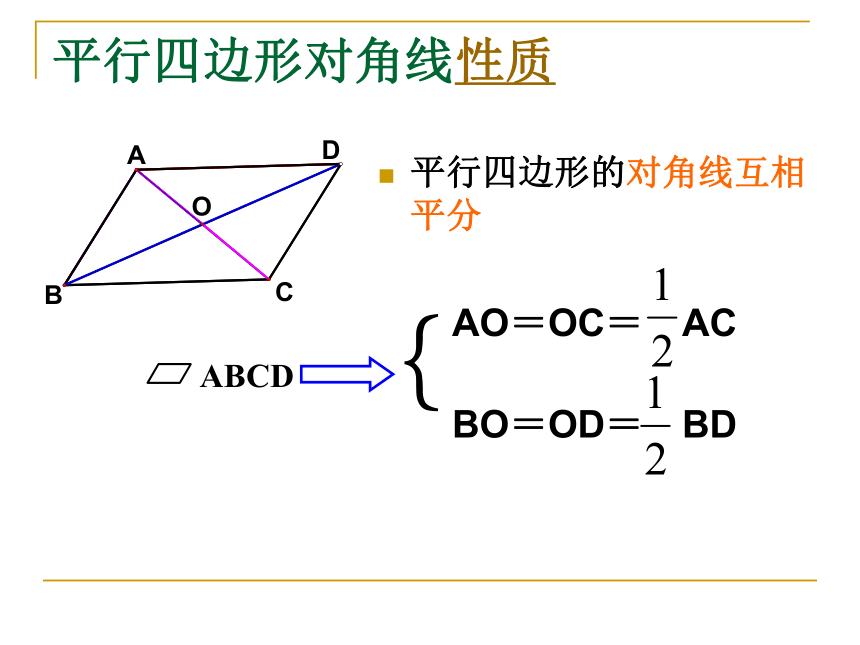
进一步的,你能发现OA与OC、OB与OD的关系吗?猜想:平行四边形的对角线互相平分OAO=BO DO=CO你能证实自己的猜想吗?推理平行四边形对角线性质平行四边形的对角线互相平分
例2 如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及 ABCD的面积。 知识运用 ◆归纳知识大收盘平行四边形的性质有:平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的对角线互相平分平行四边形的邻角互补AB=CD;AD=BCAB∥CD;AD∥BCOA=OC;OB=OD小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。练习完成课本第95页的练习 题1、2如图,在 ABCD中,AC与DB相交于点O,
∠ODA=90°,OA=6㎝,OB=3㎝。
求:AC,AD的长解:∵四边形ABCD是平行四边形
∴AC=2AO=12㎝∵四边形ABCD是平行四边形
∴DO=OB=3㎝
∵∠ODA=90°
∴在 ABCD中,AC与BD相交于点O,
AD=5,AC=8,BD=6
则 ABCD的面积为 。在 ABCD中, ∠B的平分线BE交AD于E,BC=5,AB=3,
则ED的长为 。解:在□ ABCD中在△AOB中BO-AO<AB<AO+BO既1 <AB <11平行四边形的一边长为5cm,则它的对角线可能是( )
A、4cm和6cm B、4cm和14cm
C、4cm和8cm D、10㎝和2 0㎝
在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1 请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?无数种,这些墨线都过对角线的交点回归生活: 小结:1、平行四边形定义
2、平行四边形的表示
3、平行四边形的性质(对边、对角、对角线)
◆ 上节课我们掌握了平行四边形的哪些性质?复习回顾:两组对边分别平行的四边形叫做平行四边形
平行四边形不相邻的两个顶点连成的线段叫它的对角线记作: ABCD 读作:平行四边形ABCDOAB//CDAD//BC四边形ABCD是平行四边形平行四边形的性质观察平行四边形的四条边及其四个内角,你能发现哪些结论?
平行四边形的对边平行且相等
平行四边形的对角相等ABCD AB∥CD、AD//BCABCD AB=CD、AD=BCABCD ∠A=∠C、∠B=∠D
探究2:在纸上画□ABCD,将它剪下.再在一张纸上沿□ABCD的边缘画出一个与□ABCD相同的□EFGH.在它们的中心O(两条对角线的交点)钉一个图钉.将□ABCD绕点O旋转180°,它还和□EFGH重合吗?你能从中看出前面得到的□ABCD的边角关系吗?
进一步的,你能发现OA与OC、OB与OD的关系吗?猜想:平行四边形的对角线互相平分OAO=BO DO=CO你能证实自己的猜想吗?推理平行四边形对角线性质平行四边形的对角线互相平分
例2 如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及 ABCD的面积。 知识运用 ◆归纳知识大收盘平行四边形的性质有:平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的对角线互相平分平行四边形的邻角互补AB=CD;AD=BCAB∥CD;AD∥BCOA=OC;OB=OD小结:平行四边形的性质是证明线段相等和角相等的重要依据和方法。练习完成课本第95页的练习 题1、2如图,在 ABCD中,AC与DB相交于点O,
∠ODA=90°,OA=6㎝,OB=3㎝。
求:AC,AD的长解:∵四边形ABCD是平行四边形
∴AC=2AO=12㎝∵四边形ABCD是平行四边形
∴DO=OB=3㎝
∵∠ODA=90°
∴在 ABCD中,AC与BD相交于点O,
AD=5,AC=8,BD=6
则 ABCD的面积为 。在 ABCD中, ∠B的平分线BE交AD于E,BC=5,AB=3,
则ED的长为 。解:在□ ABCD中在△AOB中BO-AO<AB<AO+BO既1 <AB <11平行四边形的一边长为5cm,则它的对角线可能是( )
A、4cm和6cm B、4cm和14cm
C、4cm和8cm D、10㎝和2 0㎝
在 ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1 请你为张师傅弹一条墨线,将锯下的这块平行四边形木板分成面积相等的两部分。你有多少种方法?无数种,这些墨线都过对角线的交点回归生活: 小结:1、平行四边形定义
2、平行四边形的表示
3、平行四边形的性质(对边、对角、对角线)
