河北省张家口市桥西区2022-2023学年八年级(上)数学期末模拟测试(含答案及详解)
文档属性
| 名称 | 河北省张家口市桥西区2022-2023学年八年级(上)数学期末模拟测试(含答案及详解) |  | |
| 格式 | zip | ||
| 文件大小 | 503.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 16:17:49 | ||
图片预览




文档简介
张家口市桥西区2022-2023学年八年级(上)数学期末模拟测试
一、选择题(本题共16个小题,共 42分。1~10小题各3分,11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 下列防疫的图标中是轴对称图形的是( )
A. B. C. D.
2. 计算(4a3 12a2b 8a3b2) ÷ (4a2)的结果是( )
A. a 3b 2ab2 B. a2 3b 2ab
C. a 2ab D. 1.5a 3b
3. 最近科学家发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为( )
A. B. C. D.
4. 若分式有意义,则x应该满足的条件是( )
A. B. C. D.
5. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A. 7cm B. 3cm C. 9cm D. 5cm
6. 如与的乘积中不含的一次项,则的值为( )
A. B. 3 C. 0 D. 1
7. 下列从左到右的运算是因式分解的是( )
A. 2x2﹣2x﹣1=2x(x﹣1)﹣1 B. 4a2+4a+1=(2a+1)2
C. (a+b)(a﹣b)=a2﹣b2 D. x2+y2=(x+y)2﹣2xy
8. 如果关于x的方程无解,则m的值是( )
A. 2 B. 0 C. 1 D. –2
9. 下列关于分式的判断中错误的是( )
A. 当时,有意义 B. 当时,的值为0
C. 无论x为何值,的值总为正数 D. 无论x为何值,不可能得整数值
10. 如图,△ABC≌△ADE,且AE∥BD,∠BAD=94°,则∠BAC的度数的值为( )
A. 84° B. 60° C. 48° D. 43°
11. 计算a﹣2b2 (a2b﹣2)﹣2正确的结果是( )
A. B. C. a6b6 D.
12. △ABC中,∠C=90°,∠A的平分线交BC于点D,如果AB=8,CD=3,则△ABD的面积为( )
A. 24 B. 12 C. 8 D. 6
13. 如图,在Rt△ACD和Rt△BEC中,若AD=BE,DC=EC,则不正确的结论是( ).
A. Rt△ACD和Rt△BCE全等 B. OA=OB
C. E是AC的中点 D. AE=BD
14. 若一个凸多边形的每一个外角都等于36°,则这个多边形的内角和是( )
A. 1080° B. 1260° C. 1440° D. 1620°
15. 如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上一动点,若AB=7,AC=6,BC=8,则△APC周长的最小值是( )
A. 13 B. 14 C. 15 D. 13.5
16. 寒假到了,为了让同学们过一个充实而有意义假期,老师推荐给大家一本好书.已知小芳每天比小荣多看5页书,并且小芳看80页书所用的天数与小荣看70页书所用的天数相等,若设小芳每天看书x页,则根据题意可列出方程( )
A. B.
C. D.
二.填空题(本大题共3题,总计 12分)
17. 计算:(﹣2a2)3的结果是_____.
18. 已知a和b两个有理数,规定一种新运算“*”为:a*b=(其中a+b≠0),若m*=﹣,则m=______.
19. 如图,在正方形中,,延长到点,使,连接,动点从点出发,以每秒的速度沿向终点运动.设点的运动时间为秒,当和全等时,的值为 __.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. (1)计算:
(2)分解因式:
21. 先化简,再求值,其中|x|=2.
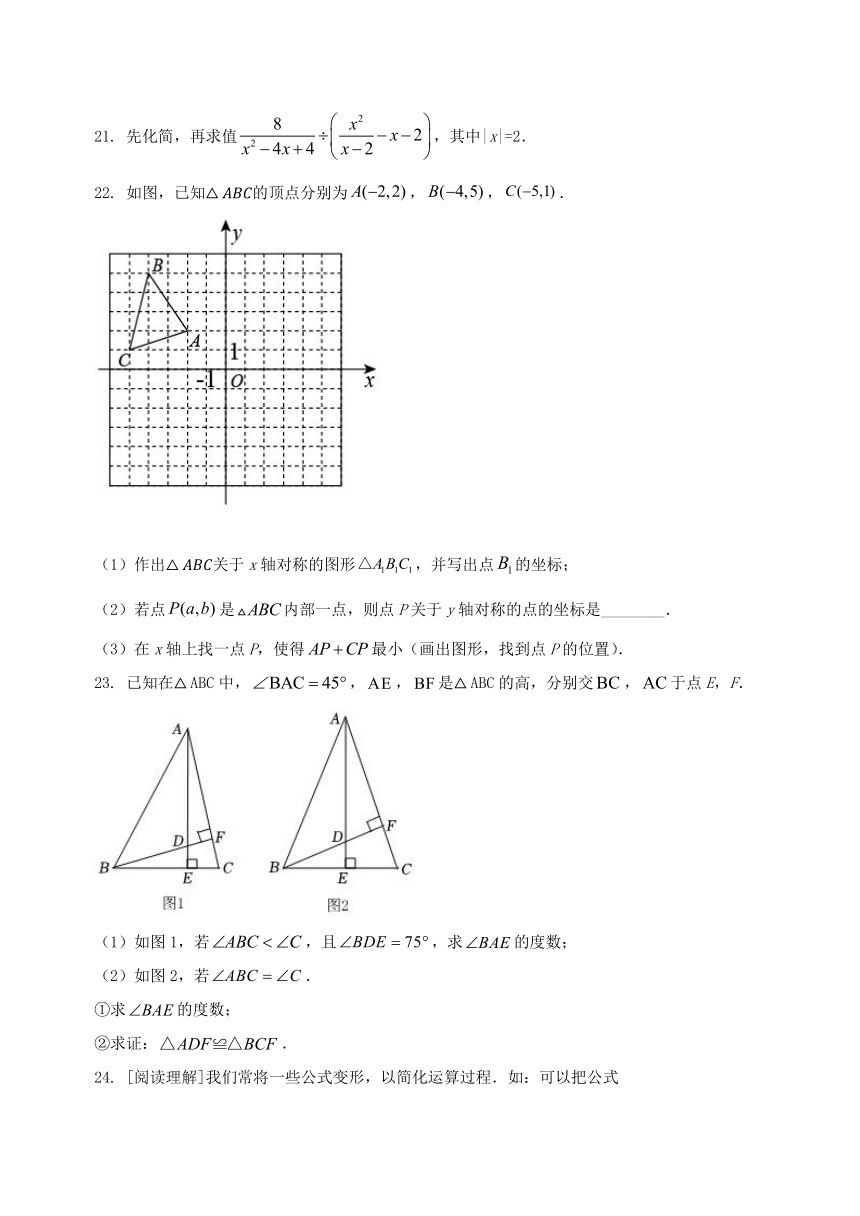
22. 如图,已知的顶点分别为,,.
(1)作出关于x轴对称的图形,并写出点的坐标;
(2)若点是内部一点,则点P关于y轴对称的点的坐标是________.
(3)在x轴上找一点P,使得最小(画出图形,找到点P的位置).
23. 已知在中,,,是的高,分别交,于点E,F.
(1)如图1,若,且,求的度数;
(2)如图2,若.
①求的度数;
②求证:.
24. [阅读理解]我们常将一些公式变形,以简化运算过程.如:可以把公式“”变形成或等形式,
问题:若x满足,求的值.
我们可以作如下解答;设,,则,
即:.
所以.
请根据你对上述内容的理解,解答下列问题:
(1)若x满足,求的值.
(2)若x满足,求的值.
25. 某县要修筑一条长为6000米的乡村旅游公路,准备承包给甲、乙两个工程队来合作完成,已知甲队每天筑路的长度是乙队的2倍,前期两队各完成了400米时,甲比乙少用了5天.
(1)求甲、乙两个工程队每天各筑路多少米?
(2)若甲队每天的工程费用为1.5万元,乙队每天的工程费用为0.9万元,要使完成全部工程的总费用不超过120万元,则至少要安排甲队筑路多少天?
26. 如图,点P、Q分别是等边边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连接AQ、CP求证:
(2)如图1,当点P、Q分别在AB、BC边上运动时,AQ、CP相交于点M,大小是否变化?若变化,请说明理由;若不变,求出它的度数
(3)如图2,当点P、Q在AB、BC的延长线上运动时,直线AQ、CP相交于M,的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
张家口市桥西区2022-2023学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:轴对称图形定义:把一个图形沿某条直线对折,对折后直线两旁的部分能完全重合.发现A,B,D都不符合定义,所以A,B,D都错误,只有C符合,所以C正确.
故答案为C.
2.【答案】:A
【解析】:解:(4a3 12a2b 8a3b2) ÷ (4a2)
.
故选A
3.【答案】:C
【解析】:数据0.00000456用科学记数法表示为:.
故选:C.
4.【答案】:B
【解析】:解:由题意,得x+1≠0,解得:x≠-1,
故选:B.
5.【答案】:B
【解析】:当长是3cm的边是底边时,三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是:13﹣3﹣3=7(cm),而3+3<7,不满足三角形的三边关系.
故底边长:3cm.
故选:B.
6.【答案】:A
【解析】:,
又与的乘积中不含的一次项,
,
解得.
故选:A.
7.【答案】:B
【解析】:解:A、没把一个多项式转化成几个整式积的形式,故本选项错误;
B、把一个多项式转化成几个整式积的形式,故本选项正确;
C、是整式的乘法,故本选项错误;
D、没把一个多项式转化成几个整式积的形式,故本选项错误;
故选:B.
8.【答案】:A
【解析】:解:方程去分母得:m+1﹣x=0,
解得x=m+1,
当分式方程分母为0,即x=3时,方程无解,
则m+1=3,
解得m=2.
故选A.
9.【答案】:D
【解析】:A选项,当时,有意义,故不符合题意;
B选项,当时,的值为0,故不符合题意;
C选项,,则无论x为何值,的值总为正数,故不符合题意;
D选项,当时,,故符合题意;
故选:D.
10.【答案】:D
【解析】:∵△ABC≌△ADE,∠BAD=94°,
∴AB=AD,∠BAC=∠DAE,
∴∠ABD=∠ADB=×(180°﹣94°)=43°,
∵AE//BD,
∴∠DAE=∠ADB=43°,
∴∠BAC=∠DAE=43°.
故选:D.
11.【答案】:B
【解析】:原式=,
故选B.
【画龙点睛】本题考查了幂的混合运算,掌握幂的运算法则是解题的关键.
12.【答案】:B
【解析】:作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3,
∴△ABD的面积为×3×8=12,
故选:B.
13.【答案】:C
【解析】:解:A.∵∠C=∠C=90°,
∴△ACD和△BCE是直角三角形,
在Rt△ACD和Rt△BCE中,
∵AD=BE,DC=CE,
∴Rt△ACD≌Rt△BCE(HL),正确;
B.∵Rt△ACD≌Rt△BCE,
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,
在△AOE和△BOD中,
∵
∴△AOE≌△BOD(AAS),
∴AO=OB,正确,不符合题意;
C.AE=BD,CE=CD,不能推出AE=CE,错误,符合题意;
D.∵Rt△ACD≌Rt△BCE,
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,正确,不符合题意.
故选C.
14.【答案】:C
【解析】:该多边形的变数为
此多边形内角和为
故选C
15.【答案】:A
【解析】:∵直线m是△ABC中BC边的垂直平分线,
∴BP=PC
∴△APC周长=AC+AP+PC=AC+AP+BP
∵两点之间线段最短,
∴AP+BP≥AB
∴△APC的周长=AC+AP+BP≥AC+AB
∵AC=6,AB=7
∴△APC周长最小为AC+AB=13
故选:A.
16.【答案】:D
【解析】:解:设小芳每天看书x页,则小荣每天看页,
由题意得: ,
故选:D.
二. 填空题
17.【答案】: ﹣8a6
【解析】:解:(﹣2a2)3
=(-2)3 (a2)3
=﹣8a6,
故答案为:﹣8a6.
18.【答案】:
【解析】:解:已知等式利用题中的新定义化简得: ,即
整理得:3(2m+3)=﹣5(2m﹣3),
去括号得:6m+9=﹣10m+15,
移项合并得:16m=6,
解得: ,
检验当时, ,
∴是分式方程的解,
则.
故答案为:.
19.【答案】: 2或7
【解析】:∵正方形ABCD,
∴
是直角三角形,
为直角三角形,
点只能在上或者上,
当点在上时,如图,当时,有,
,
,
,
当点在上时,则当时,有,
,
故答案为:2或7.
三.解答题
20【答案】:
(1)
(2)
【解析】:
【小问1详解】
解:原式;
【小问2详解】
解:原式.
【画龙点睛】本题考查了整式的混合运算、因式分解,熟练掌握运算法则是解题的关键.
21【答案】:
,
【解析】:
=
=
=
=;
∵,
∴,
∵,
∴,
∴原式=.
22【答案】:
(1)图见解析,点的坐标为;
(2);
(3)见解析.
【解析】:
(1)分别找出A,B,C关于x轴对称的点A1,B1,C1,再顺次连接点即可;
(2)利用“关于谁对称谁不变,不关谁对称谁全变”可求出P的对称点坐标;
(3)过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.
【小问1详解】
解:先找出点A,B,C关于x轴对称的点A1,B1,C1,再顺次连接A1,B1,C1.
如图所示,即为所求:
的坐标为.
【小问2详解】
解:∵P关于y轴对称,则纵坐标不变,横坐标变成原来的相反数,
∴点P关于y轴对称的点的坐标是.
【小问3详解】
解:过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.点P如图所示:
【画龙点睛】本题考查作轴对称图形,找关于坐标轴对称的点的坐标,以及动点问题.关键是掌握画轴对称图形的方法:先找对称点,再连线;熟记关于坐标轴对称的点的坐标变化特征;利用对称性解决动点问题.
23【答案】:
(1)30° (2)①;②见解析
【解析】:
【小问1详解】
∵BF⊥AC,
∴∠AFB=90°,
∵∠BAC=45°,
∴∠ABF=90°-∠BAC=45°,
∵∠BDE=75°,
∴∠BAE=∠BDE-∠ABF=30°;
【小问2详解】
①∵∠ABC=∠C,
∴AB=AC,
∵AE⊥BC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=22.5°;
②证明:∵∠BAC=45°,BF⊥AC,
∴∠AFB=90°,
∴∠ABF=∠BAC=45°,
∴FA=FB,
∵BF⊥AC,AE⊥BC,
∴∠CFB=∠AFD=∠AEC=90°,
∴∠C+∠CAE=90°,∠ADF+∠CAE=90°,
∴∠ADF=∠C,
在△ADF和△BCF中,
,
∴△ADF≌△BCF(AAS).
24【答案】:
(1)120 (2)2021
【解析】:
【小问1详解】
设,,
则,
所以,
【小问2详解】
设,,
则
所以,
25【答案】:
(1)甲每天筑路80米,乙每天筑路40米;
(2)甲至少要筑路50天
【解析】:
解:(1)设乙队每天筑路x米,则甲每天筑路2x米.
依题意,得:,
解得:x=40,
经检验:x=40是原分式方程的解,
则2x=80,
答:甲每天筑路80米,乙每天筑路40米;
(2)设甲筑路t天,则乙筑路天数为天,
依题意:,
解得:,
∴甲至少要筑路50天.
【画龙点睛】本题考查了分式方程的应用以及一元一次不等式的应用,分析题意,找到合适的数量关系列出方程或不等式是解决问题的关键.
26【答案】:
(1)证明见解析;(2)不变;60°;(3)不变;120°.
【解析】:
解:(1)证明:∵三角形ABC为等边三角形,
∴AB=AC,∠ABC=∠CAB=60°,
∵点P、点Q以相同的速度,同时从点A、点B出发,
∴BQ=AP,
在△ABQ与△CAB中,
∴.
(2)角度不变,60°,理由如下:
∵
∴∠CPA=∠AQB,
在△AMP中,
∠AMP=180°-(∠MAP+∠CPA)=180°-(∠MAP+∠AQB)=∠ABC=60°,
∴∠QMC=∠AMP=60°,
故∠QMC的度数不变,度数为60°.
(3)角度不变,120°,理由如下:
当点P、Q在AB、BC的延长线上运动时,
有AP=BQ,∴BP=CQ
∵∠ABC=∠BCA=60°,
∴∠CBP=∠ACQ=120°,
∴
∴∠Q=∠P,
∵∠QCM=∠BCP,
∴∠QMC=∠CBP=120°,
故∠QMC的度数不变,度数为120°.
一、选择题(本题共16个小题,共 42分。1~10小题各3分,11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 下列防疫的图标中是轴对称图形的是( )
A. B. C. D.
2. 计算(4a3 12a2b 8a3b2) ÷ (4a2)的结果是( )
A. a 3b 2ab2 B. a2 3b 2ab
C. a 2ab D. 1.5a 3b
3. 最近科学家发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为( )
A. B. C. D.
4. 若分式有意义,则x应该满足的条件是( )
A. B. C. D.
5. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )
A. 7cm B. 3cm C. 9cm D. 5cm
6. 如与的乘积中不含的一次项,则的值为( )
A. B. 3 C. 0 D. 1
7. 下列从左到右的运算是因式分解的是( )
A. 2x2﹣2x﹣1=2x(x﹣1)﹣1 B. 4a2+4a+1=(2a+1)2
C. (a+b)(a﹣b)=a2﹣b2 D. x2+y2=(x+y)2﹣2xy
8. 如果关于x的方程无解,则m的值是( )
A. 2 B. 0 C. 1 D. –2
9. 下列关于分式的判断中错误的是( )
A. 当时,有意义 B. 当时,的值为0
C. 无论x为何值,的值总为正数 D. 无论x为何值,不可能得整数值
10. 如图,△ABC≌△ADE,且AE∥BD,∠BAD=94°,则∠BAC的度数的值为( )
A. 84° B. 60° C. 48° D. 43°
11. 计算a﹣2b2 (a2b﹣2)﹣2正确的结果是( )
A. B. C. a6b6 D.
12. △ABC中,∠C=90°,∠A的平分线交BC于点D,如果AB=8,CD=3,则△ABD的面积为( )
A. 24 B. 12 C. 8 D. 6
13. 如图,在Rt△ACD和Rt△BEC中,若AD=BE,DC=EC,则不正确的结论是( ).
A. Rt△ACD和Rt△BCE全等 B. OA=OB
C. E是AC的中点 D. AE=BD
14. 若一个凸多边形的每一个外角都等于36°,则这个多边形的内角和是( )
A. 1080° B. 1260° C. 1440° D. 1620°
15. 如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上一动点,若AB=7,AC=6,BC=8,则△APC周长的最小值是( )
A. 13 B. 14 C. 15 D. 13.5
16. 寒假到了,为了让同学们过一个充实而有意义假期,老师推荐给大家一本好书.已知小芳每天比小荣多看5页书,并且小芳看80页书所用的天数与小荣看70页书所用的天数相等,若设小芳每天看书x页,则根据题意可列出方程( )
A. B.
C. D.
二.填空题(本大题共3题,总计 12分)
17. 计算:(﹣2a2)3的结果是_____.
18. 已知a和b两个有理数,规定一种新运算“*”为:a*b=(其中a+b≠0),若m*=﹣,则m=______.
19. 如图,在正方形中,,延长到点,使,连接,动点从点出发,以每秒的速度沿向终点运动.设点的运动时间为秒,当和全等时,的值为 __.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. (1)计算:
(2)分解因式:
21. 先化简,再求值,其中|x|=2.
22. 如图,已知的顶点分别为,,.
(1)作出关于x轴对称的图形,并写出点的坐标;
(2)若点是内部一点,则点P关于y轴对称的点的坐标是________.
(3)在x轴上找一点P,使得最小(画出图形,找到点P的位置).
23. 已知在中,,,是的高,分别交,于点E,F.
(1)如图1,若,且,求的度数;
(2)如图2,若.
①求的度数;
②求证:.
24. [阅读理解]我们常将一些公式变形,以简化运算过程.如:可以把公式“”变形成或等形式,
问题:若x满足,求的值.
我们可以作如下解答;设,,则,
即:.
所以.
请根据你对上述内容的理解,解答下列问题:
(1)若x满足,求的值.
(2)若x满足,求的值.
25. 某县要修筑一条长为6000米的乡村旅游公路,准备承包给甲、乙两个工程队来合作完成,已知甲队每天筑路的长度是乙队的2倍,前期两队各完成了400米时,甲比乙少用了5天.
(1)求甲、乙两个工程队每天各筑路多少米?
(2)若甲队每天的工程费用为1.5万元,乙队每天的工程费用为0.9万元,要使完成全部工程的总费用不超过120万元,则至少要安排甲队筑路多少天?
26. 如图,点P、Q分别是等边边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连接AQ、CP求证:
(2)如图1,当点P、Q分别在AB、BC边上运动时,AQ、CP相交于点M,大小是否变化?若变化,请说明理由;若不变,求出它的度数
(3)如图2,当点P、Q在AB、BC的延长线上运动时,直线AQ、CP相交于M,的大小是否变化?若变化,请说明理由;若不变,求出它的度数.
张家口市桥西区2022-2023学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:轴对称图形定义:把一个图形沿某条直线对折,对折后直线两旁的部分能完全重合.发现A,B,D都不符合定义,所以A,B,D都错误,只有C符合,所以C正确.
故答案为C.
2.【答案】:A
【解析】:解:(4a3 12a2b 8a3b2) ÷ (4a2)
.
故选A
3.【答案】:C
【解析】:数据0.00000456用科学记数法表示为:.
故选:C.
4.【答案】:B
【解析】:解:由题意,得x+1≠0,解得:x≠-1,
故选:B.
5.【答案】:B
【解析】:当长是3cm的边是底边时,三边为3cm,5cm,5cm,等腰三角形成立;
当长是3cm的边是腰时,底边长是:13﹣3﹣3=7(cm),而3+3<7,不满足三角形的三边关系.
故底边长:3cm.
故选:B.
6.【答案】:A
【解析】:,
又与的乘积中不含的一次项,
,
解得.
故选:A.
7.【答案】:B
【解析】:解:A、没把一个多项式转化成几个整式积的形式,故本选项错误;
B、把一个多项式转化成几个整式积的形式,故本选项正确;
C、是整式的乘法,故本选项错误;
D、没把一个多项式转化成几个整式积的形式,故本选项错误;
故选:B.
8.【答案】:A
【解析】:解:方程去分母得:m+1﹣x=0,
解得x=m+1,
当分式方程分母为0,即x=3时,方程无解,
则m+1=3,
解得m=2.
故选A.
9.【答案】:D
【解析】:A选项,当时,有意义,故不符合题意;
B选项,当时,的值为0,故不符合题意;
C选项,,则无论x为何值,的值总为正数,故不符合题意;
D选项,当时,,故符合题意;
故选:D.
10.【答案】:D
【解析】:∵△ABC≌△ADE,∠BAD=94°,
∴AB=AD,∠BAC=∠DAE,
∴∠ABD=∠ADB=×(180°﹣94°)=43°,
∵AE//BD,
∴∠DAE=∠ADB=43°,
∴∠BAC=∠DAE=43°.
故选:D.
11.【答案】:B
【解析】:原式=,
故选B.
【画龙点睛】本题考查了幂的混合运算,掌握幂的运算法则是解题的关键.
12.【答案】:B
【解析】:作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3,
∴△ABD的面积为×3×8=12,
故选:B.
13.【答案】:C
【解析】:解:A.∵∠C=∠C=90°,
∴△ACD和△BCE是直角三角形,
在Rt△ACD和Rt△BCE中,
∵AD=BE,DC=CE,
∴Rt△ACD≌Rt△BCE(HL),正确;
B.∵Rt△ACD≌Rt△BCE,
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,
在△AOE和△BOD中,
∵
∴△AOE≌△BOD(AAS),
∴AO=OB,正确,不符合题意;
C.AE=BD,CE=CD,不能推出AE=CE,错误,符合题意;
D.∵Rt△ACD≌Rt△BCE,
∴∠B=∠A,CB=CA,
∵CD=CE,
∴AE=BD,正确,不符合题意.
故选C.
14.【答案】:C
【解析】:该多边形的变数为
此多边形内角和为
故选C
15.【答案】:A
【解析】:∵直线m是△ABC中BC边的垂直平分线,
∴BP=PC
∴△APC周长=AC+AP+PC=AC+AP+BP
∵两点之间线段最短,
∴AP+BP≥AB
∴△APC的周长=AC+AP+BP≥AC+AB
∵AC=6,AB=7
∴△APC周长最小为AC+AB=13
故选:A.
16.【答案】:D
【解析】:解:设小芳每天看书x页,则小荣每天看页,
由题意得: ,
故选:D.
二. 填空题
17.【答案】: ﹣8a6
【解析】:解:(﹣2a2)3
=(-2)3 (a2)3
=﹣8a6,
故答案为:﹣8a6.
18.【答案】:
【解析】:解:已知等式利用题中的新定义化简得: ,即
整理得:3(2m+3)=﹣5(2m﹣3),
去括号得:6m+9=﹣10m+15,
移项合并得:16m=6,
解得: ,
检验当时, ,
∴是分式方程的解,
则.
故答案为:.
19.【答案】: 2或7
【解析】:∵正方形ABCD,
∴
是直角三角形,
为直角三角形,
点只能在上或者上,
当点在上时,如图,当时,有,
,
,
,
当点在上时,则当时,有,
,
故答案为:2或7.
三.解答题
20【答案】:
(1)
(2)
【解析】:
【小问1详解】
解:原式;
【小问2详解】
解:原式.
【画龙点睛】本题考查了整式的混合运算、因式分解,熟练掌握运算法则是解题的关键.
21【答案】:
,
【解析】:
=
=
=
=;
∵,
∴,
∵,
∴,
∴原式=.
22【答案】:
(1)图见解析,点的坐标为;
(2);
(3)见解析.
【解析】:
(1)分别找出A,B,C关于x轴对称的点A1,B1,C1,再顺次连接点即可;
(2)利用“关于谁对称谁不变,不关谁对称谁全变”可求出P的对称点坐标;
(3)过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.
【小问1详解】
解:先找出点A,B,C关于x轴对称的点A1,B1,C1,再顺次连接A1,B1,C1.
如图所示,即为所求:
的坐标为.
【小问2详解】
解:∵P关于y轴对称,则纵坐标不变,横坐标变成原来的相反数,
∴点P关于y轴对称的点的坐标是.
【小问3详解】
解:过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.点P如图所示:
【画龙点睛】本题考查作轴对称图形,找关于坐标轴对称的点的坐标,以及动点问题.关键是掌握画轴对称图形的方法:先找对称点,再连线;熟记关于坐标轴对称的点的坐标变化特征;利用对称性解决动点问题.
23【答案】:
(1)30° (2)①;②见解析
【解析】:
【小问1详解】
∵BF⊥AC,
∴∠AFB=90°,
∵∠BAC=45°,
∴∠ABF=90°-∠BAC=45°,
∵∠BDE=75°,
∴∠BAE=∠BDE-∠ABF=30°;
【小问2详解】
①∵∠ABC=∠C,
∴AB=AC,
∵AE⊥BC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=22.5°;
②证明:∵∠BAC=45°,BF⊥AC,
∴∠AFB=90°,
∴∠ABF=∠BAC=45°,
∴FA=FB,
∵BF⊥AC,AE⊥BC,
∴∠CFB=∠AFD=∠AEC=90°,
∴∠C+∠CAE=90°,∠ADF+∠CAE=90°,
∴∠ADF=∠C,
在△ADF和△BCF中,
,
∴△ADF≌△BCF(AAS).
24【答案】:
(1)120 (2)2021
【解析】:
【小问1详解】
设,,
则,
所以,
【小问2详解】
设,,
则
所以,
25【答案】:
(1)甲每天筑路80米,乙每天筑路40米;
(2)甲至少要筑路50天
【解析】:
解:(1)设乙队每天筑路x米,则甲每天筑路2x米.
依题意,得:,
解得:x=40,
经检验:x=40是原分式方程的解,
则2x=80,
答:甲每天筑路80米,乙每天筑路40米;
(2)设甲筑路t天,则乙筑路天数为天,
依题意:,
解得:,
∴甲至少要筑路50天.
【画龙点睛】本题考查了分式方程的应用以及一元一次不等式的应用,分析题意,找到合适的数量关系列出方程或不等式是解决问题的关键.
26【答案】:
(1)证明见解析;(2)不变;60°;(3)不变;120°.
【解析】:
解:(1)证明:∵三角形ABC为等边三角形,
∴AB=AC,∠ABC=∠CAB=60°,
∵点P、点Q以相同的速度,同时从点A、点B出发,
∴BQ=AP,
在△ABQ与△CAB中,
∴.
(2)角度不变,60°,理由如下:
∵
∴∠CPA=∠AQB,
在△AMP中,
∠AMP=180°-(∠MAP+∠CPA)=180°-(∠MAP+∠AQB)=∠ABC=60°,
∴∠QMC=∠AMP=60°,
故∠QMC的度数不变,度数为60°.
(3)角度不变,120°,理由如下:
当点P、Q在AB、BC的延长线上运动时,
有AP=BQ,∴BP=CQ
∵∠ABC=∠BCA=60°,
∴∠CBP=∠ACQ=120°,
∴
∴∠Q=∠P,
∵∠QCM=∠BCP,
∴∠QMC=∠CBP=120°,
故∠QMC的度数不变,度数为120°.
同课章节目录
