河北省张家口市下花园区2022-2023学年八年级(上)数学期末模拟测试(含答案及详解)
文档属性
| 名称 | 河北省张家口市下花园区2022-2023学年八年级(上)数学期末模拟测试(含答案及详解) |  | |
| 格式 | zip | ||
| 文件大小 | 717.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 16:18:04 | ||
图片预览



文档简介
张家口市下花园区2022-2023学年八年级(上)数学期末模拟测试
一、选择题(本题共16个小题,共 42分。1~10小题各3分,11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 下列图形中,轴对称图形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 下列运算正确的是( )
A. B.
C. D.
3. 如图所示是番茄果肉细胞结构图,番茄果肉细胞的直径约为0.0006米,将0.0006米用科学记数法表示为( )
A. 6×10-4米 B. 6×10-3米 C. 6×104米 D. 6×10-5米
4. 以下列各组线段的长为边能组成三角形的是( )
A. 2、5、8 B. 2、5、3 C. 6、6、2 D. 9、6、2
5. 如与的乘积中不含的一次项,则的值为( )
A. B. 3 C. 0 D. 1
6. 如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A. SSS B. SAS C. AAS D. ASA
7. 下列长度的三条线段,能组成三角形的是( )
A. 3,5,6 B. 3,2,1 C. 2,2,4 D. 3,6,10
8. 如图,已知在中,,,嘉淇通过尺规作图得到,交于点D,根据其作图痕迹,可得的度数为( )
A. 120° B. 110° C. 100° D. 98°
9. 下列说法中,正确的个数有( )
①若一个多边形的外角和等于360°,则这个多边形的边数为4;
②三角形的高相交于三角形的内部;
③三角形的一个外角大于任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加;
⑤对角线共有5条的多边形是五边形.
A. 1个 B. 2个 C. 3个 D. 4个
10. 如图,在ΔABC中,DE是AC的垂直平分线,AE=3cm,ΔABD的周长为13cm,则ΔABC的周长是( )
A. 13cm B. 16cm C. 19cm D. 22cm
11. 如图,,下列等式不一定正确的是( )
A. B. C. D.
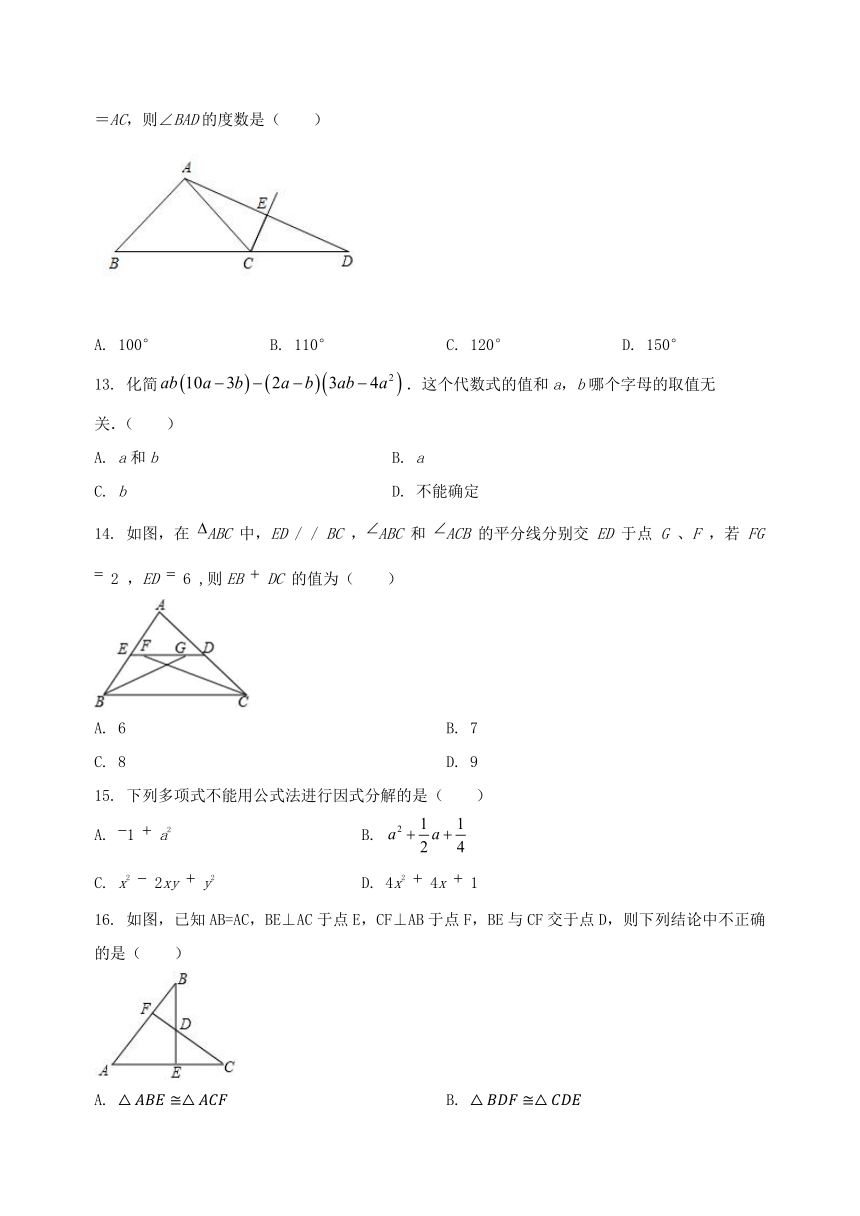
12. 如图,在△ABD中,∠D=20°,CE垂直平分AD,交BD于点C,交AD于点E,连接AC,若AB=AC,则∠BAD的度数是( )
A. 100° B. 110° C. 120° D. 150°
13. 化简.这个代数式的值和a,b哪个字母的取值无关.( )
A. a和b B. a
C. b D. 不能确定
14. 如图,在 ABC 中,ED / / BC ,ABC 和 ACB 的平分线分别交 ED 于点 G 、F ,若 FG 2 ,ED 6 ,则EB DC 的值为( )
A. 6 B. 7
C. 8 D. 9
15. 下列多项式不能用公式法进行因式分解的是( )
A. 1 a2 B.
C. x2 2xy y2 D. 4x2 4x 1
16. 如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
A. B.
C. 点D在平分线上 D. 点D是CF的中点
二.填空题(本大题共3题,总计 12分)
17. 已知.
(1)a的值为___________;
(2)若,则___________.
18. 已知三角形的三边长分别为3,5,x,则化简式子|x-2|+|x-9|=___.
19. 如图,在中,与相交于点F,且,则之间的数量关系是_____________.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. (1)计算:
(2)雯雯在计算时,解答过程如下:
…………第一步 …………第二步 …………第三步
雯雯的解答从第______步开始出错,请写出正确的解题过程.
21. 已知(x+y)2=1,(x﹣y)2=49,求x2+y2与y的值.
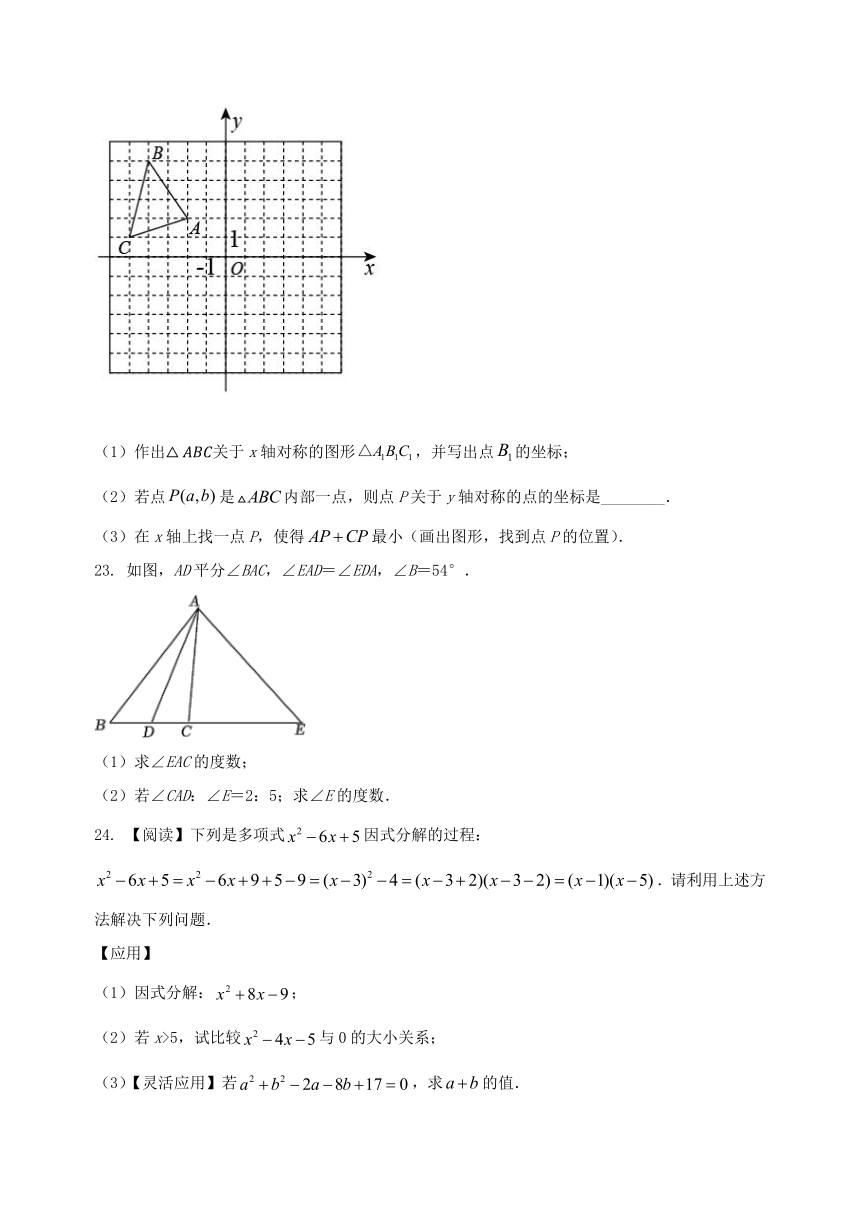
22. 如图,已知的顶点分别为,,.
(1)作出关于x轴对称的图形,并写出点的坐标;
(2)若点是内部一点,则点P关于y轴对称的点的坐标是________.
(3)在x轴上找一点P,使得最小(画出图形,找到点P的位置).
23. 如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°.
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
24. 【阅读】下列是多项式因式分解的过程:.请利用上述方法解决下列问题.
【应用】
(1)因式分解:;
(2)若x>5,试比较与0的大小关系;
(3)【灵活应用】若,求的值.
25. 刘峰和李明相约周末去科技馆看展览,根据他们的谈话内容,试求李明乘公交车、刘峰骑自行车每小时各行多少千米?
刘峰:我查好地图了,你看看 李明:好的,我家门口的公交车站,正好有一趟到科技馆那站停的车,我坐明天的车.
刘峰:从地图上看,我家到科技馆的距离比你家近10千米,我就骑自行车去了. 李明:行,根据我的经验,公交车的速度一般是你骑自行车速度的3倍,那你明天早上点从家出发,如顺利,咱俩同时到达.
26. 已知M是等边△ABC的边BC上的点.
(1)如图①,过点M作MN∥CA,交AB于点N,求证:BM = BN;
(2)如图②,连接AM,过点M作∠AMH = 60°,MH与∠ACB的邻补角的平分线交于点H,过点H作HD⊥BC,交BC延长线于点D.
(ⅰ)求证:MA = MH;
(ⅱ)直接写出CB,CM,CD之间的数量关系式.
张家口市下花园区2022-2023学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:第1个是轴对称图形;
第2个是轴对称图形;
第3个不是轴对称图形;
第4个是轴对称图形;
故选C.
【画龙点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】:D
【解析】:A、,故不符合题意;
B 、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
故选:D.
3.【答案】:A
【解析】:解:0.0006=6×10-4,
故选:A.
4.【答案】:C
【解析】:解:根据三角形任意两边的和大于第三边,可知:
A、2+5<8,不能够组成三角形,故不符合题意;
B、2+3=5,不能组成三角形,故不符合题意;
C、2+6>7,能组成三角形,故符合题意;
D、2+6<9,不能组成三角形,故不符合题意;
故选:C.
5.【答案】:A
【解析】:,
又与的乘积中不含的一次项,
,
解得.
故选:A.
6.【答案】:D
【解析】:解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:D.
7.【答案】:A
【解析】:A. ∵3+5>6,∴长度为3,5,6的三条线段能组成三角形,故该选项符合题意,
B. ∵1+2=3,∴长度为3,2,1的三条线段不能组成三角形,故该选项不符合题意,
C. ∵2+2=4,∴长度为2,2,4的三条线段不能组成三角形,故该选项不符合题意,
D. ∵3+6<10,∴长度为3,6,10三条线段不能组成三角形,故该选项不符合题意,
故选A
8.【答案】:B
【解析】:根据作图痕迹可知,是∠ABC的平分线,
∵,,
∴
∵是∠ABC的平分线,
∴
∴
故选:B.
9.【答案】:B
【解析】:解:①任意多边形的外角和等于360°,说法错误,不符合题意;
②只有锐角三角形的高相交于三角形的内部,说法错误,不符合题意;
③根据三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和,得三角形的一个外角大于任意一个于它不相邻的内角,说法错误,不符合题意;
④根据多边形内角和公式:,得一个多边形的边数每增加一条,这个多边形的内角和就增加180°,说法正确,符合题意;
⑤n边形的对角线条数为:,当n=5时,,说法正确,符合题意;
综上,正确个数有2个,
故选B.
10.【答案】:C
【解析】:解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故选:C.
11.【答案】:D
【解析】:,
,,,,
,
,
即只有选项符合题意,选项A、选项B、选项C都不符合题意;
故选:D.
12.【答案】:C
【解析】:解:∵CE垂直平分AD,
∴,
∴,
∴,
∵AB=AC,
∴,
∴,
∴,
故选:C.
13.【答案】:C
【解析】:
,
则这个代数式的值与字母b的取值无关,
故选:C.
14.【答案】:C
【解析】:∵ED∥BC,
∴∠EGB=∠GBC,∠DFC=∠FCB,
∵∠GBC=∠GBE,∠FCB=∠FCD,
∴∠EGB=∠EBG,∠DCF=∠DFC,
∴BE=EG,CD=DF,
∵FG=2,ED=6,
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8,
故选C.
15.【答案】:B
【解析】:解:, 故A不符合题意;
不能用公式法分解因式,故B符合题意;
x2 2xy y2, 故C不符合题意;
, 故D不符合题意;
故选:B
16.【答案】:D
【解析】:解:A、∵AB=AC,BE⊥AC于E,CF⊥AB于F,∠A=∠A∴△ABE≌△ACF(AAS),正确;
B∵△ABE≌△ACF,AB=AC∴BF=CE,∠B=∠C,∠DFB=∠DEC=90°∴△BDF≌△CDE(ASA),正确;
C、∵△ABE≌△ACF,AB=AC∴BF=CE,∠B=∠C,∠DFB=∠DEC=90°∴DF=DE故点D在∠BAC的平分线上,正确;
D、无法判定,错误;
故选D.
【画龙点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL. 注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
二. 填空题
17.【答案】: ①. 1 ②. 3
【解析】:解:(1)
故答案为:1;
(2)当,时,
故答案为:3.
18.【答案】: 7
【解析】:解:根据题意,得5 3即2∴x-2>0,x-9<0,
∴|x-2|+|x-9|=x-2-(x-9)=7.
故答案为7.
19.【答案】:
【解析】:先利用同角的余角相等得到=,再通过证,得到即,再 利用三角形内角和得可得,最后利用角的和差即可得到答案,=.
证明:∵,
∴,
∴=
又∵,
∴
∴即
∵
∴即
∴=
故答案为:.
三.解答题
20【答案】:
(1);(2)一,见解析
【解析】:
(1)
;
(2)一,
m(1+m) (m 1)2
=m+m2 (m2 2m+1)
=m+m2 m2+2m 1
=3m 1.
21【答案】:
,的值为或或或
【解析】:
解:∵①,②,
∴①+②得:,解得;
∵,
或,
,
或,
或或或,
解得或或或,
,的值为或或或.
【画龙点睛】此题考查了完全平方公式、平方根的运用,熟练掌握完全平方公式和平方根的运算是解本题的关键.
22【答案】:
(1)图见解析,点的坐标为;
(2);
(3)见解析.
【解析】:
(1)分别找出A,B,C关于x轴对称的点A1,B1,C1,再顺次连接点即可;
(2)利用“关于谁对称谁不变,不关谁对称谁全变”可求出P的对称点坐标;
(3)过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.
【小问1详解】
解:先找出点A,B,C关于x轴对称的点A1,B1,C1,再顺次连接A1,B1,C1.
如图所示,即为所求:
的坐标为.
【小问2详解】
解:∵P关于y轴对称,则纵坐标不变,横坐标变成原来的相反数,
∴点P关于y轴对称的点的坐标是.
【小问3详解】
解:过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.点P如图所示:
【画龙点睛】本题考查作轴对称图形,找关于坐标轴对称的点的坐标,以及动点问题.关键是掌握画轴对称图形的方法:先找对称点,再连线;熟记关于坐标轴对称的点的坐标变化特征;利用对称性解决动点问题.
23【答案】:
(1)∠EAC=54°;
(2).
【解析】:
【小问1详解】
∵∠EAD=∠EDA,
∴∠EAC+∠CAD=∠B+∠BAD,
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∴∠EAC=∠B.
∵∠B=54°,
∴∠EAC=54°.
【小问2详解】
设∠CAD=2x,则∠E=5x,∠DAB=2x,
∵∠B=54°,
∴∠EDA=∠EAD=2x+54°.
∵∠EDA+∠EAD+∠E=180°,
∴2x+54°+2x+54°+5x=180°.
解得x=8°.
∴∠E=5x=40°.
24【答案】:
(1)
(2)
(3)5
【解析】:
【小问1详解】
解:,
【小问2详解】
解:,,
∴x+1>0,x-5>0,
,
;
【小问3详解】
解:,
,
∵,
∴,
,,
.
25【答案】:
刘峰骑自行车每小时行20千米,李明乘公交车每小时行60千米
【解析】:
解:设刘峰骑自行车每小时行x千米,则李明乘公交车每小时行千米,
根据题意,得,
解得,
经检验,是所列分式方程的解,且符合题意,
∴(千米/时),
答:刘峰骑自行车每小时行20千米,李明乘公交车每小时行60千米.
26【答案】:
(1)见解析 (2)(ⅰ)见解析;(ⅱ)BC CM 2CD
【解析】:
∴△AMN≌△MHC(ASA),
∴MA=MH;
(ⅱ)CB=CM+2CD;理由如下:
证明:如图2,过M点作MG⊥AB于G,
∵△AMN≌△MHC,
∴MN=HC,
∵△BMN为等边三角形,MG⊥AB
∴MN=MB,BM=2BG,
∴HC=BM,
△BMG和△CHD中
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∴BM=2CD,
所以BC=MC+2CD.
【画龙点睛】此题主要考查了等边三角形的性质,以及全等三角形的判定与性质,关键是正确作出辅助线,熟练掌握证明三角形全等的方法.
一、选择题(本题共16个小题,共 42分。1~10小题各3分,11~16小题各2分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1. 下列图形中,轴对称图形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 下列运算正确的是( )
A. B.
C. D.
3. 如图所示是番茄果肉细胞结构图,番茄果肉细胞的直径约为0.0006米,将0.0006米用科学记数法表示为( )
A. 6×10-4米 B. 6×10-3米 C. 6×104米 D. 6×10-5米
4. 以下列各组线段的长为边能组成三角形的是( )
A. 2、5、8 B. 2、5、3 C. 6、6、2 D. 9、6、2
5. 如与的乘积中不含的一次项,则的值为( )
A. B. 3 C. 0 D. 1
6. 如图,小明书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么小明画图的依据是( )
A. SSS B. SAS C. AAS D. ASA
7. 下列长度的三条线段,能组成三角形的是( )
A. 3,5,6 B. 3,2,1 C. 2,2,4 D. 3,6,10
8. 如图,已知在中,,,嘉淇通过尺规作图得到,交于点D,根据其作图痕迹,可得的度数为( )
A. 120° B. 110° C. 100° D. 98°
9. 下列说法中,正确的个数有( )
①若一个多边形的外角和等于360°,则这个多边形的边数为4;
②三角形的高相交于三角形的内部;
③三角形的一个外角大于任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加;
⑤对角线共有5条的多边形是五边形.
A. 1个 B. 2个 C. 3个 D. 4个
10. 如图,在ΔABC中,DE是AC的垂直平分线,AE=3cm,ΔABD的周长为13cm,则ΔABC的周长是( )
A. 13cm B. 16cm C. 19cm D. 22cm
11. 如图,,下列等式不一定正确的是( )
A. B. C. D.
12. 如图,在△ABD中,∠D=20°,CE垂直平分AD,交BD于点C,交AD于点E,连接AC,若AB=AC,则∠BAD的度数是( )
A. 100° B. 110° C. 120° D. 150°
13. 化简.这个代数式的值和a,b哪个字母的取值无关.( )
A. a和b B. a
C. b D. 不能确定
14. 如图,在 ABC 中,ED / / BC ,ABC 和 ACB 的平分线分别交 ED 于点 G 、F ,若 FG 2 ,ED 6 ,则EB DC 的值为( )
A. 6 B. 7
C. 8 D. 9
15. 下列多项式不能用公式法进行因式分解的是( )
A. 1 a2 B.
C. x2 2xy y2 D. 4x2 4x 1
16. 如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
A. B.
C. 点D在平分线上 D. 点D是CF的中点
二.填空题(本大题共3题,总计 12分)
17. 已知.
(1)a的值为___________;
(2)若,则___________.
18. 已知三角形的三边长分别为3,5,x,则化简式子|x-2|+|x-9|=___.
19. 如图,在中,与相交于点F,且,则之间的数量关系是_____________.
三.解答题(共7题,总计66分,解答应写出文字说明、证明过程或演算步骤)
20. (1)计算:
(2)雯雯在计算时,解答过程如下:
…………第一步 …………第二步 …………第三步
雯雯的解答从第______步开始出错,请写出正确的解题过程.
21. 已知(x+y)2=1,(x﹣y)2=49,求x2+y2与y的值.
22. 如图,已知的顶点分别为,,.
(1)作出关于x轴对称的图形,并写出点的坐标;
(2)若点是内部一点,则点P关于y轴对称的点的坐标是________.
(3)在x轴上找一点P,使得最小(画出图形,找到点P的位置).
23. 如图,AD平分∠BAC,∠EAD=∠EDA,∠B=54°.
(1)求∠EAC的度数;
(2)若∠CAD:∠E=2:5;求∠E的度数.
24. 【阅读】下列是多项式因式分解的过程:.请利用上述方法解决下列问题.
【应用】
(1)因式分解:;
(2)若x>5,试比较与0的大小关系;
(3)【灵活应用】若,求的值.
25. 刘峰和李明相约周末去科技馆看展览,根据他们的谈话内容,试求李明乘公交车、刘峰骑自行车每小时各行多少千米?
刘峰:我查好地图了,你看看 李明:好的,我家门口的公交车站,正好有一趟到科技馆那站停的车,我坐明天的车.
刘峰:从地图上看,我家到科技馆的距离比你家近10千米,我就骑自行车去了. 李明:行,根据我的经验,公交车的速度一般是你骑自行车速度的3倍,那你明天早上点从家出发,如顺利,咱俩同时到达.
26. 已知M是等边△ABC的边BC上的点.
(1)如图①,过点M作MN∥CA,交AB于点N,求证:BM = BN;
(2)如图②,连接AM,过点M作∠AMH = 60°,MH与∠ACB的邻补角的平分线交于点H,过点H作HD⊥BC,交BC延长线于点D.
(ⅰ)求证:MA = MH;
(ⅱ)直接写出CB,CM,CD之间的数量关系式.
张家口市下花园区2022-2023学年八年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:第1个是轴对称图形;
第2个是轴对称图形;
第3个不是轴对称图形;
第4个是轴对称图形;
故选C.
【画龙点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】:D
【解析】:A、,故不符合题意;
B 、,故不符合题意;
C、,故不符合题意;
D、,故符合题意;
故选:D.
3.【答案】:A
【解析】:解:0.0006=6×10-4,
故选:A.
4.【答案】:C
【解析】:解:根据三角形任意两边的和大于第三边,可知:
A、2+5<8,不能够组成三角形,故不符合题意;
B、2+3=5,不能组成三角形,故不符合题意;
C、2+6>7,能组成三角形,故符合题意;
D、2+6<9,不能组成三角形,故不符合题意;
故选:C.
5.【答案】:A
【解析】:,
又与的乘积中不含的一次项,
,
解得.
故选:A.
6.【答案】:D
【解析】:解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:D.
7.【答案】:A
【解析】:A. ∵3+5>6,∴长度为3,5,6的三条线段能组成三角形,故该选项符合题意,
B. ∵1+2=3,∴长度为3,2,1的三条线段不能组成三角形,故该选项不符合题意,
C. ∵2+2=4,∴长度为2,2,4的三条线段不能组成三角形,故该选项不符合题意,
D. ∵3+6<10,∴长度为3,6,10三条线段不能组成三角形,故该选项不符合题意,
故选A
8.【答案】:B
【解析】:根据作图痕迹可知,是∠ABC的平分线,
∵,,
∴
∵是∠ABC的平分线,
∴
∴
故选:B.
9.【答案】:B
【解析】:解:①任意多边形的外角和等于360°,说法错误,不符合题意;
②只有锐角三角形的高相交于三角形的内部,说法错误,不符合题意;
③根据三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和,得三角形的一个外角大于任意一个于它不相邻的内角,说法错误,不符合题意;
④根据多边形内角和公式:,得一个多边形的边数每增加一条,这个多边形的内角和就增加180°,说法正确,符合题意;
⑤n边形的对角线条数为:,当n=5时,,说法正确,符合题意;
综上,正确个数有2个,
故选B.
10.【答案】:C
【解析】:解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故选:C.
11.【答案】:D
【解析】:,
,,,,
,
,
即只有选项符合题意,选项A、选项B、选项C都不符合题意;
故选:D.
12.【答案】:C
【解析】:解:∵CE垂直平分AD,
∴,
∴,
∴,
∵AB=AC,
∴,
∴,
∴,
故选:C.
13.【答案】:C
【解析】:
,
则这个代数式的值与字母b的取值无关,
故选:C.
14.【答案】:C
【解析】:∵ED∥BC,
∴∠EGB=∠GBC,∠DFC=∠FCB,
∵∠GBC=∠GBE,∠FCB=∠FCD,
∴∠EGB=∠EBG,∠DCF=∠DFC,
∴BE=EG,CD=DF,
∵FG=2,ED=6,
∴EB+CD=EG+DF=EF+FG+FG+DG=ED+FG=8,
故选C.
15.【答案】:B
【解析】:解:, 故A不符合题意;
不能用公式法分解因式,故B符合题意;
x2 2xy y2, 故C不符合题意;
, 故D不符合题意;
故选:B
16.【答案】:D
【解析】:解:A、∵AB=AC,BE⊥AC于E,CF⊥AB于F,∠A=∠A∴△ABE≌△ACF(AAS),正确;
B∵△ABE≌△ACF,AB=AC∴BF=CE,∠B=∠C,∠DFB=∠DEC=90°∴△BDF≌△CDE(ASA),正确;
C、∵△ABE≌△ACF,AB=AC∴BF=CE,∠B=∠C,∠DFB=∠DEC=90°∴DF=DE故点D在∠BAC的平分线上,正确;
D、无法判定,错误;
故选D.
【画龙点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL. 注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
二. 填空题
17.【答案】: ①. 1 ②. 3
【解析】:解:(1)
故答案为:1;
(2)当,时,
故答案为:3.
18.【答案】: 7
【解析】:解:根据题意,得5 3
∴|x-2|+|x-9|=x-2-(x-9)=7.
故答案为7.
19.【答案】:
【解析】:先利用同角的余角相等得到=,再通过证,得到即,再 利用三角形内角和得可得,最后利用角的和差即可得到答案,=.
证明:∵,
∴,
∴=
又∵,
∴
∴即
∵
∴即
∴=
故答案为:.
三.解答题
20【答案】:
(1);(2)一,见解析
【解析】:
(1)
;
(2)一,
m(1+m) (m 1)2
=m+m2 (m2 2m+1)
=m+m2 m2+2m 1
=3m 1.
21【答案】:
,的值为或或或
【解析】:
解:∵①,②,
∴①+②得:,解得;
∵,
或,
,
或,
或或或,
解得或或或,
,的值为或或或.
【画龙点睛】此题考查了完全平方公式、平方根的运用,熟练掌握完全平方公式和平方根的运算是解本题的关键.
22【答案】:
(1)图见解析,点的坐标为;
(2);
(3)见解析.
【解析】:
(1)分别找出A,B,C关于x轴对称的点A1,B1,C1,再顺次连接点即可;
(2)利用“关于谁对称谁不变,不关谁对称谁全变”可求出P的对称点坐标;
(3)过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.
【小问1详解】
解:先找出点A,B,C关于x轴对称的点A1,B1,C1,再顺次连接A1,B1,C1.
如图所示,即为所求:
的坐标为.
【小问2详解】
解:∵P关于y轴对称,则纵坐标不变,横坐标变成原来的相反数,
∴点P关于y轴对称的点的坐标是.
【小问3详解】
解:过x轴作点A的对称点为A1,连接A1C交于x轴的点即为点P,使得最小.点P如图所示:
【画龙点睛】本题考查作轴对称图形,找关于坐标轴对称的点的坐标,以及动点问题.关键是掌握画轴对称图形的方法:先找对称点,再连线;熟记关于坐标轴对称的点的坐标变化特征;利用对称性解决动点问题.
23【答案】:
(1)∠EAC=54°;
(2).
【解析】:
【小问1详解】
∵∠EAD=∠EDA,
∴∠EAC+∠CAD=∠B+∠BAD,
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∴∠EAC=∠B.
∵∠B=54°,
∴∠EAC=54°.
【小问2详解】
设∠CAD=2x,则∠E=5x,∠DAB=2x,
∵∠B=54°,
∴∠EDA=∠EAD=2x+54°.
∵∠EDA+∠EAD+∠E=180°,
∴2x+54°+2x+54°+5x=180°.
解得x=8°.
∴∠E=5x=40°.
24【答案】:
(1)
(2)
(3)5
【解析】:
【小问1详解】
解:,
【小问2详解】
解:,,
∴x+1>0,x-5>0,
,
;
【小问3详解】
解:,
,
∵,
∴,
,,
.
25【答案】:
刘峰骑自行车每小时行20千米,李明乘公交车每小时行60千米
【解析】:
解:设刘峰骑自行车每小时行x千米,则李明乘公交车每小时行千米,
根据题意,得,
解得,
经检验,是所列分式方程的解,且符合题意,
∴(千米/时),
答:刘峰骑自行车每小时行20千米,李明乘公交车每小时行60千米.
26【答案】:
(1)见解析 (2)(ⅰ)见解析;(ⅱ)BC CM 2CD
【解析】:
∴△AMN≌△MHC(ASA),
∴MA=MH;
(ⅱ)CB=CM+2CD;理由如下:
证明:如图2,过M点作MG⊥AB于G,
∵△AMN≌△MHC,
∴MN=HC,
∵△BMN为等边三角形,MG⊥AB
∴MN=MB,BM=2BG,
∴HC=BM,
△BMG和△CHD中
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∴BM=2CD,
所以BC=MC+2CD.
【画龙点睛】此题主要考查了等边三角形的性质,以及全等三角形的判定与性质,关键是正确作出辅助线,熟练掌握证明三角形全等的方法.
同课章节目录
