鲁教版(五四制)数学八年级上册 第四章平面图形的镶嵌(1)教案
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 第四章平面图形的镶嵌(1)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 19:26:01 | ||
图片预览



文档简介
《平面图形的镶嵌》教学设计
课前准备:
1、教师准备:教学材料包(边长相等的正三角形、正方形、正五边形、正六边形多个,全等的任意三角形多个,全等的任意四边形多个)、磁性按钉
2、学生准备:(课前完成,并组内交流订正)
多边形的内角和计算公式
正多边形的内角计算公式
正三角形内角 、正方形内角 、正五边形内角 、正六边形内角
创设情境、认识平面镶嵌
课件展示生活中常见的地砖照片
师:我们为什么看这个?
师:因为我家的地板糟糕透了,确实该换了。我正在发愁,我应该怎样去铺我的地板呢?孩子们可以一起帮我解决这个问题么?
【本课开始展示地砖图片,拉近生活和数学的距离,再辅以上述问题,激起学生学习的兴趣。】
师:从图中发现了哪些基本图形?
生:三角形、正方形、正六边形、正三角形……
师:这些基本图形又是怎样铺满整个地面的呢?
生:紧密的贴合在一起,没有缝隙
师:铺地板中蕴藏着数学知识,数学来源于生活,又服务于生活。这就是数学知识平面图形的镶嵌,也是我们这节课所要研究的内容。
(教师板演课题,多媒体展示平面图形镶嵌的概念,学生齐读)
师:平面镶嵌的重要条件是什么?
生:用大小形状完全相同的一个或多个图形
彼此之间不重叠,不留空隙
(师板演重要条件)
【从生活中铺瓷砖的事例中,提炼出平面图形镶嵌的概念,学生便于理解。】
探索图形平面镶嵌的条件
活动(一):用同一种正多边形镶嵌
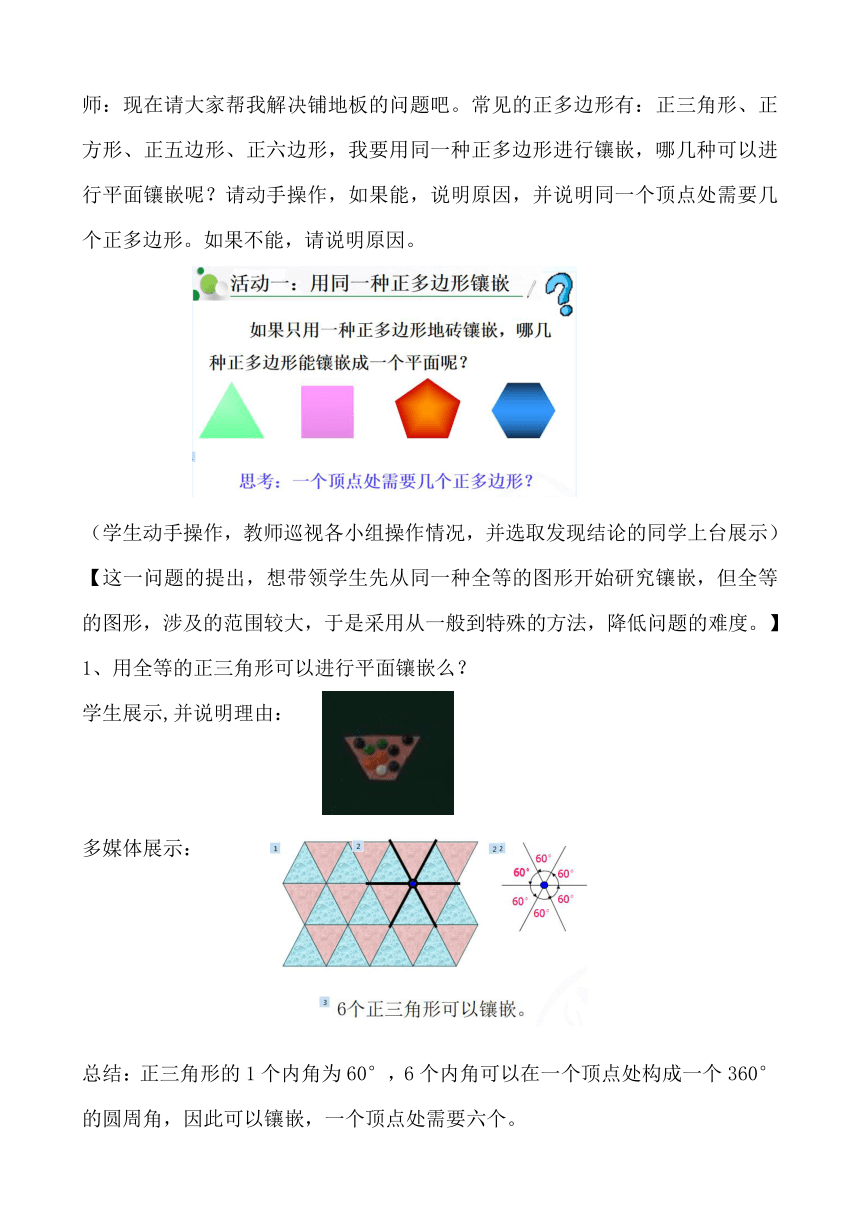
师:现在请大家帮我解决铺地板的问题吧。常见的正多边形有:正三角形、正方形、正五边形、正六边形,我要用同一种正多边形进行镶嵌,哪几种可以进行平面镶嵌呢?请动手操作,如果能,说明原因,并说明同一个顶点处需要几个正多边形。如果不能,请说明原因。
(学生动手操作,教师巡视各小组操作情况,并选取发现结论的同学上台展示)
【这一问题的提出,想带领学生先从同一种全等的图形开始研究镶嵌,但全等的图形,涉及的范围较大,于是采用从一般到特殊的方法,降低问题的难度。】
用全等的正三角形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正三角形的1个内角为60°,6个内角可以在一个顶点处构成一个360°的圆周角,因此可以镶嵌,一个顶点处需要六个。
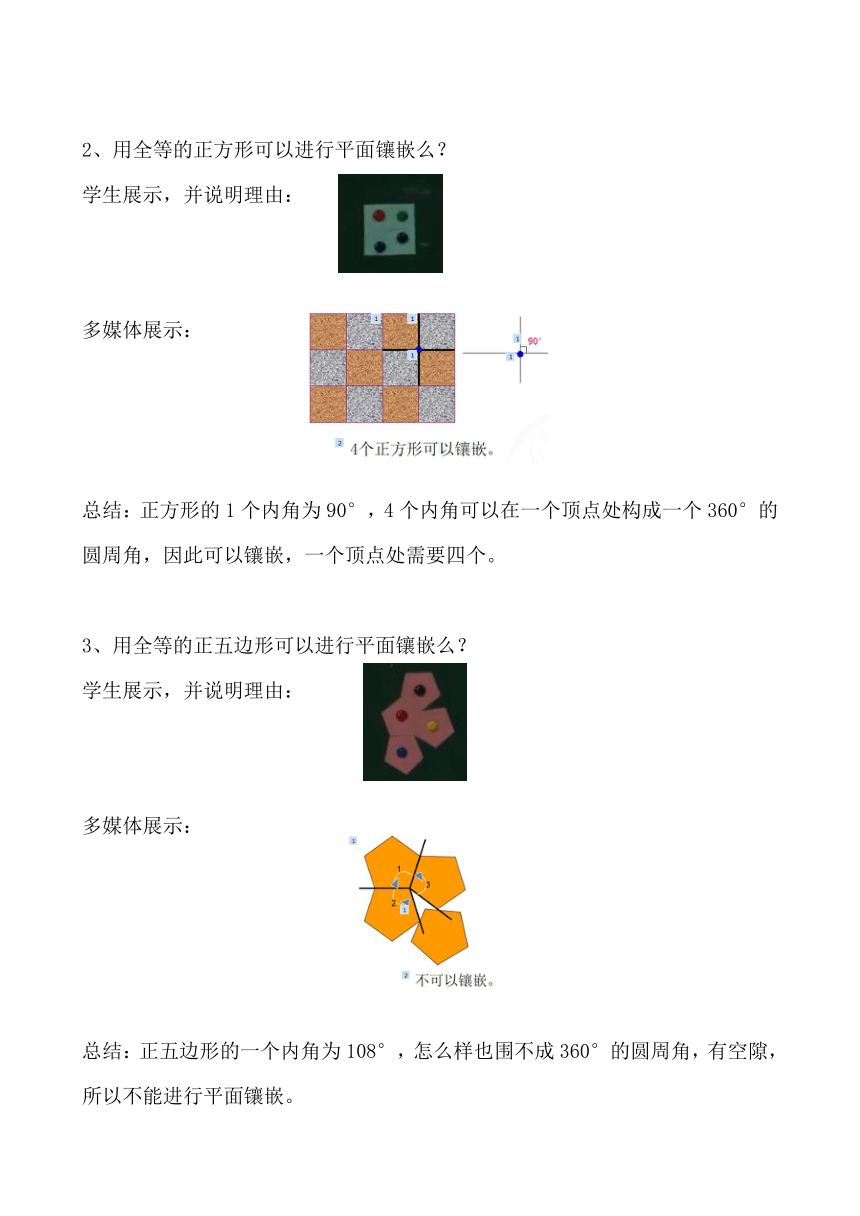
用全等的正方形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正方形的1个内角为90°,4个内角可以在一个顶点处构成一个360°的圆周角,因此可以镶嵌,一个顶点处需要四个。
用全等的正五边形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正五边形的一个内角为108°,怎么样也围不成360°的圆周角,有空隙,所以不能进行平面镶嵌。
用全等的正六边形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正六边形的1个内角为120°,3个内角可以在一个顶点处构成一个360°的圆周角,因此可以镶嵌,一个顶点处需要三个。
【“活动一”是让学生在动手实践中学习,通过“做一做”形成对图形平铺的感性认识,增加生活实践经验,引出课题,并得出正三角形、正方形、正六边形可以平铺的结论。】
思考:你还能找到可以镶嵌的其他正多边形吗 比如:正八边形?正十二边形?……
(学生独立思考,组内讨论,并展示自己的结论)
总结判断方法:求出内角,看看能不能在同一顶点处构成360°
活动一总结:
结论1:
同一种正多边形是否可以镶嵌平面的关键是:正多边形的一个内角的倍数是否为360°(使同一个顶点处的所有内角之和等于360°))
结论2:
用同一种正多边形镶嵌的图形只有正三角形,正四边形,正六边形。
【从特殊回到一般,比较几种图形的共性,用比较归纳的方法得到能够镶嵌的正多边形图形在一拼接点处所具有的特点。通过这一特点的归纳,使不同层次的学生,在交流与合作的过程中感受新知。】
活动二、用两种正多边形镶嵌
师:我突然觉得用同一种正多边形地砖来铺地有些太普通,如果用两种正多边形来铺地可不可以呢?请你选择其中两种来尝试一下,可不可以进行平面镶嵌,并说明理由。
【这一问题的设置,是将镶嵌从同一个图形拓展到多个图形研究。学生回答这个问题时,主要是通过动手操作,得出结论。】
(学生动手操作,教师巡视各小组操作情况,并选取发现结论的同学上台展示)
1、用边长相等的正三角形和正方形能平面镶嵌吗?
学生展示,并说明理由:
多媒体展示:
总结:用三个正三角形可以拼180°,再用两个正方形可以拼180°,所以拼在同一顶点处是360°,所以可以进行平面镶嵌。
师:如果你的手中没有纸片,不能进行动手操作,那该怎么办呢?我们可以用方程思想来解决一下。
解:设在一个顶点周围有m个正三角形,n个正方形。
那么,这些角的和就应该满足方程:60°m + 90°n = 360°
化简得:2m + 3n = 12
由此得到方程的正整数解为 因此可以组合镶嵌平面。
2、用边长相等的正三角形和正六边形能平面镶嵌吗?
由两学生来说明:可不可以平面镶嵌?
同一顶点处分别需要几个正三角形和正六边形?
为什么可以平面镶嵌?
多媒体展示:
总结:用1个正六边形和4个正三角形可以在同一顶点处构成360°
用2个正六边形和2个正三角形也可以在同一顶点处构成360°
所以正三角形和正六边形可以用来组合进行平面镶嵌。
师:你可不可以仿照之前的方法用方程思想来解决一下这个问题呢?
解:设一个顶点周围有m个正三角形,n个正六边形。
那么,这些角的和就应该满足方程:60°m + 120°n = 360°
化简得:m + 2n = 6
由此得到方程的正整数解为 因此可以组合镶嵌平面。
3、用边长相等的正方形和正六边形能平面镶嵌吗?
不能,学生说明原因
活动二总结:
结论:
两种正多边形能组合镶嵌的条件:使同一个顶点处的所有内角之和等于360°
师:除此之外,还有几种正多边形可以组合进行平面镶嵌,让我们一起欣赏一下:
正方形与正八边形 正五边形与正十边形
正三角形与正十二边形
活动三:用同一种任意多边形镶嵌
师:我的邻居刚刚铺完地砖,剩余了一些全等的任意三角形和任意四边形,我可不可以用它们来铺满我的院子呢?
1、用全等的任意三角形能否镶嵌平面?
学生展示,并说明理由:
多媒体展示:
总结:全等的任意三角形可以进行平面镶嵌
用全等的任意四边形能否镶嵌平面?
学生展示,并说明理由:
多媒体展示:
总结:全等的任意四边形可以进行平面镶嵌。
课堂总结
师:通过以上三个活动我们可以总结出判断一个或两个图形可以进行平面镶嵌的条件是:使同一个顶点处的所有内角之和等于360°
本节课的主要内容是:
1、掌握平面镶嵌的定义
2、通过对同一正多边形、两种正多边形、和任意三角形、四边形能否进行平面
镶嵌的动手操作与实验,得出图形能否镶嵌的条件:在同一顶点处能否拼成
360°的圆周角。这也正是本节课的学习目标。
当堂检测
学生独立完成,教师批阅,集体订正答案
五、美丽的镶嵌图案欣赏
课前准备:
1、教师准备:教学材料包(边长相等的正三角形、正方形、正五边形、正六边形多个,全等的任意三角形多个,全等的任意四边形多个)、磁性按钉
2、学生准备:(课前完成,并组内交流订正)
多边形的内角和计算公式
正多边形的内角计算公式
正三角形内角 、正方形内角 、正五边形内角 、正六边形内角
创设情境、认识平面镶嵌
课件展示生活中常见的地砖照片
师:我们为什么看这个?
师:因为我家的地板糟糕透了,确实该换了。我正在发愁,我应该怎样去铺我的地板呢?孩子们可以一起帮我解决这个问题么?
【本课开始展示地砖图片,拉近生活和数学的距离,再辅以上述问题,激起学生学习的兴趣。】
师:从图中发现了哪些基本图形?
生:三角形、正方形、正六边形、正三角形……
师:这些基本图形又是怎样铺满整个地面的呢?
生:紧密的贴合在一起,没有缝隙
师:铺地板中蕴藏着数学知识,数学来源于生活,又服务于生活。这就是数学知识平面图形的镶嵌,也是我们这节课所要研究的内容。
(教师板演课题,多媒体展示平面图形镶嵌的概念,学生齐读)
师:平面镶嵌的重要条件是什么?
生:用大小形状完全相同的一个或多个图形
彼此之间不重叠,不留空隙
(师板演重要条件)
【从生活中铺瓷砖的事例中,提炼出平面图形镶嵌的概念,学生便于理解。】
探索图形平面镶嵌的条件
活动(一):用同一种正多边形镶嵌
师:现在请大家帮我解决铺地板的问题吧。常见的正多边形有:正三角形、正方形、正五边形、正六边形,我要用同一种正多边形进行镶嵌,哪几种可以进行平面镶嵌呢?请动手操作,如果能,说明原因,并说明同一个顶点处需要几个正多边形。如果不能,请说明原因。
(学生动手操作,教师巡视各小组操作情况,并选取发现结论的同学上台展示)
【这一问题的提出,想带领学生先从同一种全等的图形开始研究镶嵌,但全等的图形,涉及的范围较大,于是采用从一般到特殊的方法,降低问题的难度。】
用全等的正三角形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正三角形的1个内角为60°,6个内角可以在一个顶点处构成一个360°的圆周角,因此可以镶嵌,一个顶点处需要六个。
用全等的正方形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正方形的1个内角为90°,4个内角可以在一个顶点处构成一个360°的圆周角,因此可以镶嵌,一个顶点处需要四个。
用全等的正五边形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正五边形的一个内角为108°,怎么样也围不成360°的圆周角,有空隙,所以不能进行平面镶嵌。
用全等的正六边形可以进行平面镶嵌么?
学生展示,并说明理由:
多媒体展示:
总结:正六边形的1个内角为120°,3个内角可以在一个顶点处构成一个360°的圆周角,因此可以镶嵌,一个顶点处需要三个。
【“活动一”是让学生在动手实践中学习,通过“做一做”形成对图形平铺的感性认识,增加生活实践经验,引出课题,并得出正三角形、正方形、正六边形可以平铺的结论。】
思考:你还能找到可以镶嵌的其他正多边形吗 比如:正八边形?正十二边形?……
(学生独立思考,组内讨论,并展示自己的结论)
总结判断方法:求出内角,看看能不能在同一顶点处构成360°
活动一总结:
结论1:
同一种正多边形是否可以镶嵌平面的关键是:正多边形的一个内角的倍数是否为360°(使同一个顶点处的所有内角之和等于360°))
结论2:
用同一种正多边形镶嵌的图形只有正三角形,正四边形,正六边形。
【从特殊回到一般,比较几种图形的共性,用比较归纳的方法得到能够镶嵌的正多边形图形在一拼接点处所具有的特点。通过这一特点的归纳,使不同层次的学生,在交流与合作的过程中感受新知。】
活动二、用两种正多边形镶嵌
师:我突然觉得用同一种正多边形地砖来铺地有些太普通,如果用两种正多边形来铺地可不可以呢?请你选择其中两种来尝试一下,可不可以进行平面镶嵌,并说明理由。
【这一问题的设置,是将镶嵌从同一个图形拓展到多个图形研究。学生回答这个问题时,主要是通过动手操作,得出结论。】
(学生动手操作,教师巡视各小组操作情况,并选取发现结论的同学上台展示)
1、用边长相等的正三角形和正方形能平面镶嵌吗?
学生展示,并说明理由:
多媒体展示:
总结:用三个正三角形可以拼180°,再用两个正方形可以拼180°,所以拼在同一顶点处是360°,所以可以进行平面镶嵌。
师:如果你的手中没有纸片,不能进行动手操作,那该怎么办呢?我们可以用方程思想来解决一下。
解:设在一个顶点周围有m个正三角形,n个正方形。
那么,这些角的和就应该满足方程:60°m + 90°n = 360°
化简得:2m + 3n = 12
由此得到方程的正整数解为 因此可以组合镶嵌平面。
2、用边长相等的正三角形和正六边形能平面镶嵌吗?
由两学生来说明:可不可以平面镶嵌?
同一顶点处分别需要几个正三角形和正六边形?
为什么可以平面镶嵌?
多媒体展示:
总结:用1个正六边形和4个正三角形可以在同一顶点处构成360°
用2个正六边形和2个正三角形也可以在同一顶点处构成360°
所以正三角形和正六边形可以用来组合进行平面镶嵌。
师:你可不可以仿照之前的方法用方程思想来解决一下这个问题呢?
解:设一个顶点周围有m个正三角形,n个正六边形。
那么,这些角的和就应该满足方程:60°m + 120°n = 360°
化简得:m + 2n = 6
由此得到方程的正整数解为 因此可以组合镶嵌平面。
3、用边长相等的正方形和正六边形能平面镶嵌吗?
不能,学生说明原因
活动二总结:
结论:
两种正多边形能组合镶嵌的条件:使同一个顶点处的所有内角之和等于360°
师:除此之外,还有几种正多边形可以组合进行平面镶嵌,让我们一起欣赏一下:
正方形与正八边形 正五边形与正十边形
正三角形与正十二边形
活动三:用同一种任意多边形镶嵌
师:我的邻居刚刚铺完地砖,剩余了一些全等的任意三角形和任意四边形,我可不可以用它们来铺满我的院子呢?
1、用全等的任意三角形能否镶嵌平面?
学生展示,并说明理由:
多媒体展示:
总结:全等的任意三角形可以进行平面镶嵌
用全等的任意四边形能否镶嵌平面?
学生展示,并说明理由:
多媒体展示:
总结:全等的任意四边形可以进行平面镶嵌。
课堂总结
师:通过以上三个活动我们可以总结出判断一个或两个图形可以进行平面镶嵌的条件是:使同一个顶点处的所有内角之和等于360°
本节课的主要内容是:
1、掌握平面镶嵌的定义
2、通过对同一正多边形、两种正多边形、和任意三角形、四边形能否进行平面
镶嵌的动手操作与实验,得出图形能否镶嵌的条件:在同一顶点处能否拼成
360°的圆周角。这也正是本节课的学习目标。
当堂检测
学生独立完成,教师批阅,集体订正答案
五、美丽的镶嵌图案欣赏
