人教版八年级上册13.3.1 等腰三角形的性质 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.1 等腰三角形的性质 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 687.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 20:27:29 | ||
图片预览





文档简介
(共18张PPT)
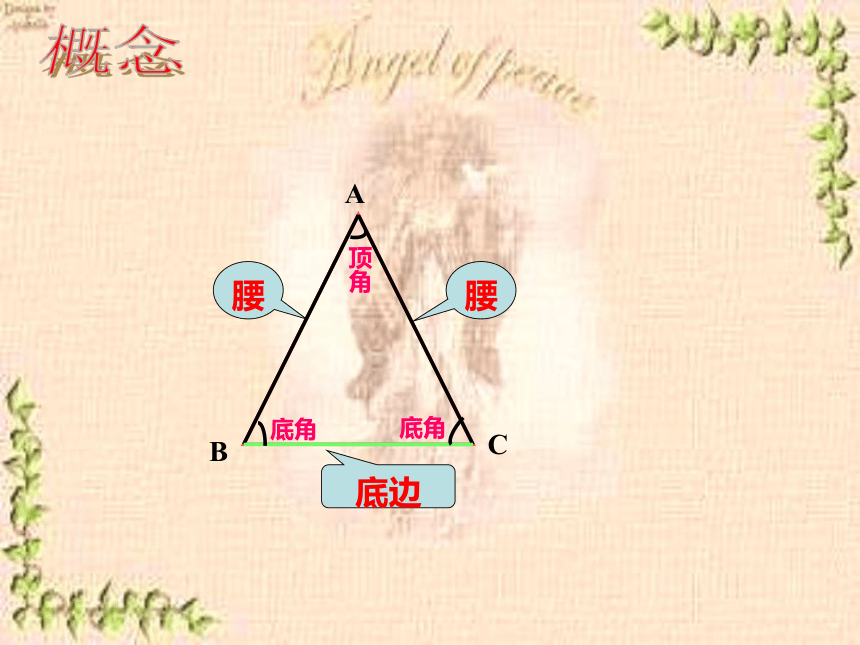
A
C
B
腰
腰
底边
顶角
底角
底角
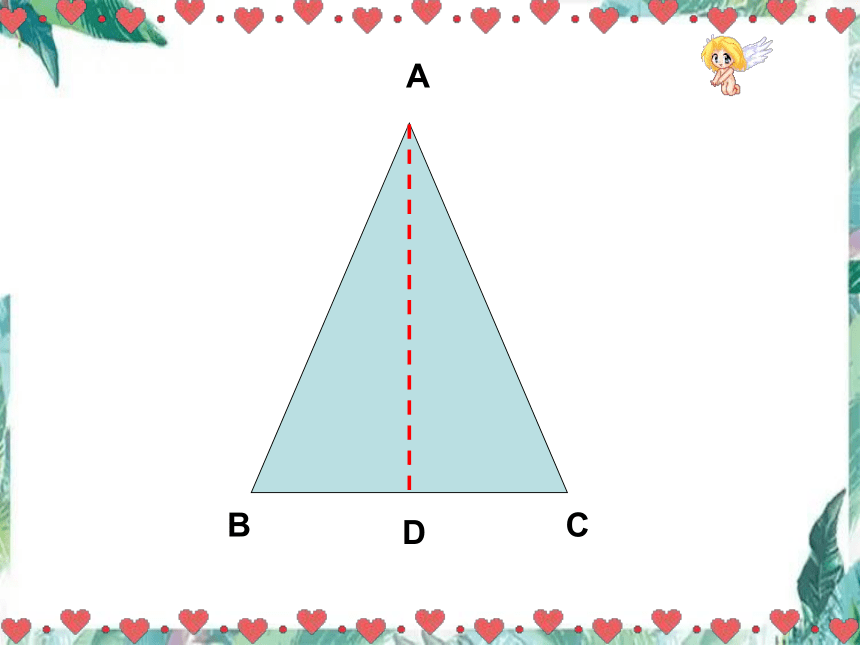
A
C
B
D
等腰三角形的两个底角相等。
猜想
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
等腰三角形的性质
如图,根据等腰三角形性质定理在△ABC中,AB=AC时,
①∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
② ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
③ ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
D
C
B
A
1、等腰三角形的顶角为40°,则它的底角为________.
2、(1)在△ABC中,AB=AC, ∠A=30°,则∠B=_______.
(2) 在△ABC中,AB=BC, ∠A=30°,则∠C=_______
小试牛刀
70°
35°
30°
3、如图,在△ABC中,AB=AC,
(1) 若∠1=∠2,BD=3,则BC=________.
(2) 若AD⊥BC,CD=5,则BD=__________.
(3) 若BD=CD, ∠1=20°,则∠BAC=________
A
B
C
1
2
D
6
5
40°
1.(1)、若等腰三角形的一个内角为80°,
则另两个角分别是________
(2)、等腰三角形的两边分别是8,6,
则这个三角形周长为________
(3)、已知等腰三角形一腰上的高与另一腰的
夹为25°,则底角度数为________。
2、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。
A
B
C
D
1、如图,已知AB∥CD,AB=AC, ∠ABC= 68° ,则∠ACD= ______.
C
D
B
A
2、如图,在△ABC中,AB=AC,点D是BC的中点,
则下列结论中错误的是( )
A:∠BAD=∠CAD B:AD⊥BC
C:∠B=∠C D:∠BAC=∠B
D
C
B
A
3、如图,在△ABC中,AB=AC, D为BC的中点,∠BAD= 35° ,则
∠C=______
D
C
B
A
我学会了…
我发现生活中…
我感受到了…
我感到最高兴的是…
这节课—
我想我将…
畅谈收获
通过本节课的学习,你学到了哪些知识?在合作学习中你感受到了什么?你还有哪些疑惑?
作业
1.课本77页练习第1,2,3题
2.选做题
如图,在△ABC中,AB=AC,点D,E分别在AC,AB边上,且BC=BD,AD=DE=EB, 求∠AD的度数.
A
B
C
D
E
A
C
B
腰
腰
底边
顶角
底角
底角
A
C
B
D
等腰三角形的两个底角相等。
猜想
等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合
等腰三角形的性质
如图,根据等腰三角形性质定理在△ABC中,AB=AC时,
①∵AD⊥BC,∴∠_____ = ∠_____,____= ____.
② ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.
③ ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.
D
C
B
A
1、等腰三角形的顶角为40°,则它的底角为________.
2、(1)在△ABC中,AB=AC, ∠A=30°,则∠B=_______.
(2) 在△ABC中,AB=BC, ∠A=30°,则∠C=_______
小试牛刀
70°
35°
30°
3、如图,在△ABC中,AB=AC,
(1) 若∠1=∠2,BD=3,则BC=________.
(2) 若AD⊥BC,CD=5,则BD=__________.
(3) 若BD=CD, ∠1=20°,则∠BAC=________
A
B
C
1
2
D
6
5
40°
1.(1)、若等腰三角形的一个内角为80°,
则另两个角分别是________
(2)、等腰三角形的两边分别是8,6,
则这个三角形周长为________
(3)、已知等腰三角形一腰上的高与另一腰的
夹为25°,则底角度数为________。
2、如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数。
A
B
C
D
1、如图,已知AB∥CD,AB=AC, ∠ABC= 68° ,则∠ACD= ______.
C
D
B
A
2、如图,在△ABC中,AB=AC,点D是BC的中点,
则下列结论中错误的是( )
A:∠BAD=∠CAD B:AD⊥BC
C:∠B=∠C D:∠BAC=∠B
D
C
B
A
3、如图,在△ABC中,AB=AC, D为BC的中点,∠BAD= 35° ,则
∠C=______
D
C
B
A
我学会了…
我发现生活中…
我感受到了…
我感到最高兴的是…
这节课—
我想我将…
畅谈收获
通过本节课的学习,你学到了哪些知识?在合作学习中你感受到了什么?你还有哪些疑惑?
作业
1.课本77页练习第1,2,3题
2.选做题
如图,在△ABC中,AB=AC,点D,E分别在AC,AB边上,且BC=BD,AD=DE=EB, 求∠AD的度数.
A
B
C
D
E
