13.3.1 等腰三角形 第1课时 等腰三角形的性质 导学案及课前练习(无答案)
文档属性
| 名称 | 13.3.1 等腰三角形 第1课时 等腰三角形的性质 导学案及课前练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 186.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 15:09:30 | ||
图片预览

文档简介
13.3.1 等腰三角形
第一课时
【学习目标】
1.记住等腰三角形的概念和性质.(重点)
2.能灵活应用等腰三角形的性质解决有关的计算和证明问题.(重点、难点)
【自主学习】
1.已知一个三角形的两边长分别为4cm,5cm,第三边长为整数.
(1)由4cm,5cm,cm为边可以组成多少个不同的三角形?为什么?
(2)如果这个三角形是等腰三角形,则的值可以是 .
【自主探究】
探究一:等腰三角形的性质
把一张长方形的纸片对折,并剪掉阴影部分(如下图),把剩下部分展开,会得到一个什么图形?在这过程中,你能得到什么结论?
在你得到的结论中,能用学过的知识加以证明吗?试一试!
【引入新知】等腰三角形的性质
几何语言:
【变式训练】
题型1:1等腰+1角(知一求二)
例1:如图,在△ABC中,AB=AC
1)若底角是30°,则它的顶角是_______
2)若顶角是30°,则它的底角是_______
3)若一个角是30°,则另两角为________________
注意:________________________________________
练习:等腰三角形一个角为70°,它的另外两个角为_____________
思考:等腰三角形一个角为120°,它的另外两个角为___________。
总结:当已知角位置未明确且是(直)钝角时,该角只能为________
题型2:两等腰+1角(边化角,知一求二)
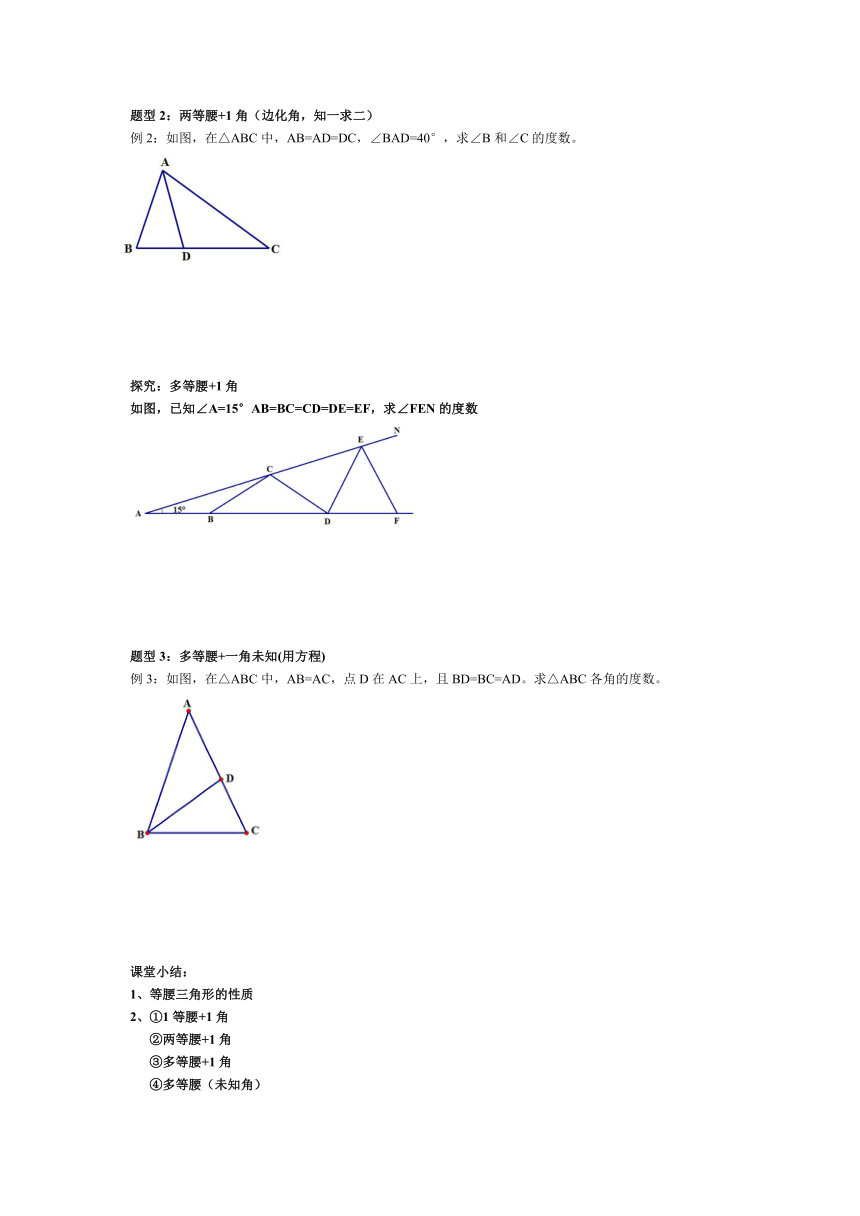
例2:如图,在△ABC中,AB=AD=DC,∠BAD=40°,求∠B和∠C的度数。
探究:多等腰+1角
如图,已知∠A=15°AB=BC=CD=DE=EF,求∠FEN的度数
题型3:多等腰+一角未知(用方程)
例3:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD。求△ABC各角的度数。
课堂小结:
1、等腰三角形的性质
2、①1等腰+1角
②两等腰+1角
③多等腰+1角
④多等腰(未知角)
自主检测
【基础训练】
1.若一个等腰三角形的周长为19,其中一边长为5,则这个三角形底边长为( )
A.9 B.5 C.5或9 D.以上都不对
2.如图4,在△ABC中,∠BAC=90,AB=AC,∠BAD=30,AD=AE,则∠EDC的度数为( )
A.10 B.12 C.15 D.20
3.如图5,在△ABC中,D为AC上一点,∠A=36,∠DBC=36,∠C=72,则图中等腰三角形的个数为( )
A.3个 B.2个 C.1个 D.0个
4.等腰三角形一腰上的高与另一腰的夹角是50,则这个等腰三角形的底角是( )
A.70 B.20 C.70或20 D.40或140
5.如图6,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为______________.
6.如图,AD=BD,AB=AC=CD,求∠BAC
7.如图,BC=ED,AB=AE,求证:AC=AD
【拓展提升】
8.如图,∠ABC=50°,∠ACB=80°,DB=BA,CE=CA,求∠D,∠E,∠DAE
9.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC与点D,求∠DBC
10.如图,点D,E,分别是AB,AC的中点,CD⊥AB,BE⊥AC,求证:AC=AB
图1
图6
图4
图5
第一课时
【学习目标】
1.记住等腰三角形的概念和性质.(重点)
2.能灵活应用等腰三角形的性质解决有关的计算和证明问题.(重点、难点)
【自主学习】
1.已知一个三角形的两边长分别为4cm,5cm,第三边长为整数.
(1)由4cm,5cm,cm为边可以组成多少个不同的三角形?为什么?
(2)如果这个三角形是等腰三角形,则的值可以是 .
【自主探究】
探究一:等腰三角形的性质
把一张长方形的纸片对折,并剪掉阴影部分(如下图),把剩下部分展开,会得到一个什么图形?在这过程中,你能得到什么结论?
在你得到的结论中,能用学过的知识加以证明吗?试一试!
【引入新知】等腰三角形的性质
几何语言:
【变式训练】
题型1:1等腰+1角(知一求二)
例1:如图,在△ABC中,AB=AC
1)若底角是30°,则它的顶角是_______
2)若顶角是30°,则它的底角是_______
3)若一个角是30°,则另两角为________________
注意:________________________________________
练习:等腰三角形一个角为70°,它的另外两个角为_____________
思考:等腰三角形一个角为120°,它的另外两个角为___________。
总结:当已知角位置未明确且是(直)钝角时,该角只能为________
题型2:两等腰+1角(边化角,知一求二)
例2:如图,在△ABC中,AB=AD=DC,∠BAD=40°,求∠B和∠C的度数。
探究:多等腰+1角
如图,已知∠A=15°AB=BC=CD=DE=EF,求∠FEN的度数
题型3:多等腰+一角未知(用方程)
例3:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD。求△ABC各角的度数。
课堂小结:
1、等腰三角形的性质
2、①1等腰+1角
②两等腰+1角
③多等腰+1角
④多等腰(未知角)
自主检测
【基础训练】
1.若一个等腰三角形的周长为19,其中一边长为5,则这个三角形底边长为( )
A.9 B.5 C.5或9 D.以上都不对
2.如图4,在△ABC中,∠BAC=90,AB=AC,∠BAD=30,AD=AE,则∠EDC的度数为( )
A.10 B.12 C.15 D.20
3.如图5,在△ABC中,D为AC上一点,∠A=36,∠DBC=36,∠C=72,则图中等腰三角形的个数为( )
A.3个 B.2个 C.1个 D.0个
4.等腰三角形一腰上的高与另一腰的夹角是50,则这个等腰三角形的底角是( )
A.70 B.20 C.70或20 D.40或140
5.如图6,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为______________.
6.如图,AD=BD,AB=AC=CD,求∠BAC
7.如图,BC=ED,AB=AE,求证:AC=AD
【拓展提升】
8.如图,∠ABC=50°,∠ACB=80°,DB=BA,CE=CA,求∠D,∠E,∠DAE
9.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC与点D,求∠DBC
10.如图,点D,E,分别是AB,AC的中点,CD⊥AB,BE⊥AC,求证:AC=AB
图1
图6
图4
图5
