人教版数学八年级上册 13.3.1等腰三角形的性质 课件 (共17张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1等腰三角形的性质 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
13.3.1 等腰三角形
——等腰三角形的性质(1)
活动一:看一看
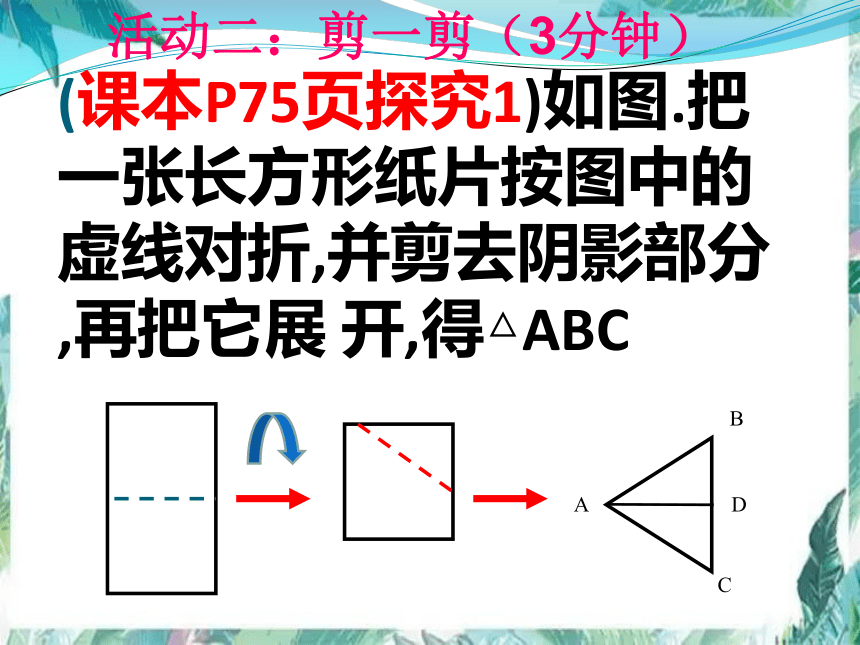
(课本P75页探究1)如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展 开,得△ABC
活动二:剪一剪(3分钟)
A
C
D
B
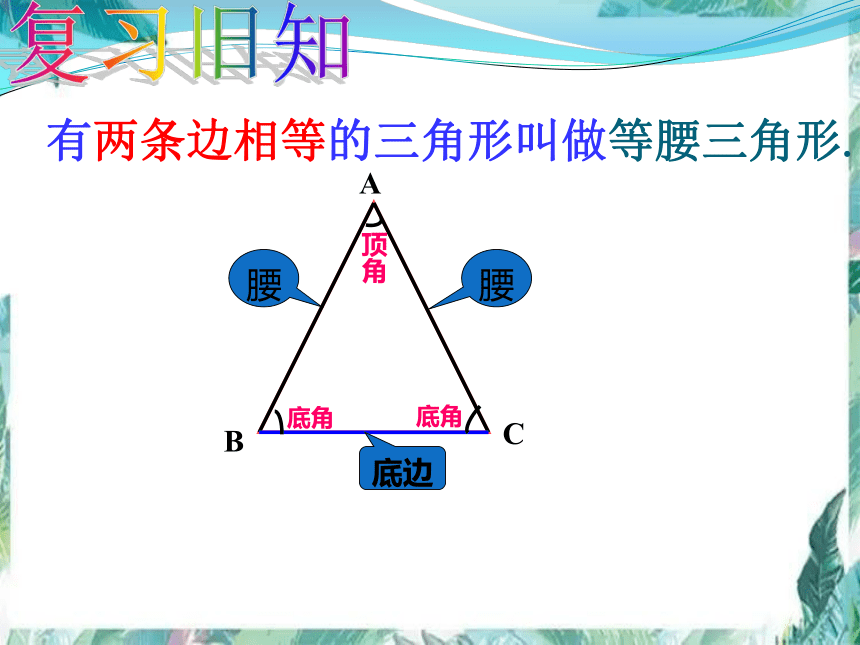
有两条边相等的三角形叫做等腰三角形.
A
C
B
腰
腰
底边
顶角
底角
底角
复习旧知
等腰三角形的两个底角相等
在 三角形中,
同一个
几何语言:
在△ABC中,
∵ AC=AB
∴ ∠B=∠C
C
A
B
?
如图,在△ABC中,AB=AC,求证:∠B=∠C
想一想:1.如何证明两个角相等?
议一议:2.如何构造两个全等三角形?
证:作△ABC对称轴AP交BC于点D
∵△ABD与△ADC关于AD轴对称
∴△ABD≌△ADC
∴∠B=∠C
D
等腰三角形性质简称:
等边对等角。
√
等边
等角
活动三:想一想
练一练:
1、判断正误(口答)
(1) 如图,在△ABC中,
∴ ∠B=∠C
∵ AB=BC
C
A
B
注意使用
“等边对等角”时,
边与角的对应关系.
∠A
2、判断正误(口答)
“等边对等角”只能在同一个三角形中使用.
(2) 如图,在△ABC中,
∵ AC=BC
∴ ∠ADC=∠BEC
C
A
B
D
E
((
((
∠A=∠B
例1:如图,在△ABC中,AB=AC
1)若底角是30°,则它的顶角是_______
2)若顶角是30°,则它的底角是_______
3)若一个角是30°,则另两角为________________
120°
75°
注意:已知角未定位置,分类讨论
题型1:1等腰+1角(知一求二)
30°
120°
75°
75°
30°,120°或75°,75°
2.等腰三角形一个角为70°,它的另外两个角为___________________;
70°,40°或 55°,55°
70°
55°
55°
70°
70°
40°
思考:等腰三角形一个角为120°,它的另外两个角为___________。
30°, 30°
等腰三角形中角的位置不明确时要分类讨论:
当给出的角是直角或钝角时,它只能是顶角
① 顶角度数+底角度数× 2 =180°
② 0°<底角度数<90°
例2:如图,在△ABC中,AB=AD=DC,
∠BAD=40°,求∠B和∠C的度数。
题型2:两等腰+1角(边化角,知一求二)
探究:如图,已知∠A=15°AB=BC=CD=DE=EF,求∠FEN的度数。
难点:
1.等腰三角形数量多
2.已知角少
突破:标角法
1.找含有已知角的等腰三角形
2.利用知一求二得出其余角
题型2:多等腰+1角(知一求二,各个击破)
题型3:多等腰+一角未知
例3:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD。求△ABC各角的度数。
(用方程)
1、等腰三角形的性质
课堂小结:
说一说,这节课你学到了哪些知识?
2、①1等腰+1角
②两等腰+1角
③多等腰+1角
④多等腰(未知角)
知一求二,分类讨论
找含已知角的等腰三角形
方程思想
作业布置:
学案《等腰三角形的性质1》
谢谢!
13.3.1 等腰三角形
——等腰三角形的性质(1)
活动一:看一看
(课本P75页探究1)如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展 开,得△ABC
活动二:剪一剪(3分钟)
A
C
D
B
有两条边相等的三角形叫做等腰三角形.
A
C
B
腰
腰
底边
顶角
底角
底角
复习旧知
等腰三角形的两个底角相等
在 三角形中,
同一个
几何语言:
在△ABC中,
∵ AC=AB
∴ ∠B=∠C
C
A
B
?
如图,在△ABC中,AB=AC,求证:∠B=∠C
想一想:1.如何证明两个角相等?
议一议:2.如何构造两个全等三角形?
证:作△ABC对称轴AP交BC于点D
∵△ABD与△ADC关于AD轴对称
∴△ABD≌△ADC
∴∠B=∠C
D
等腰三角形性质简称:
等边对等角。
√
等边
等角
活动三:想一想
练一练:
1、判断正误(口答)
(1) 如图,在△ABC中,
∴ ∠B=∠C
∵ AB=BC
C
A
B
注意使用
“等边对等角”时,
边与角的对应关系.
∠A
2、判断正误(口答)
“等边对等角”只能在同一个三角形中使用.
(2) 如图,在△ABC中,
∵ AC=BC
∴ ∠ADC=∠BEC
C
A
B
D
E
((
((
∠A=∠B
例1:如图,在△ABC中,AB=AC
1)若底角是30°,则它的顶角是_______
2)若顶角是30°,则它的底角是_______
3)若一个角是30°,则另两角为________________
120°
75°
注意:已知角未定位置,分类讨论
题型1:1等腰+1角(知一求二)
30°
120°
75°
75°
30°,120°或75°,75°
2.等腰三角形一个角为70°,它的另外两个角为___________________;
70°,40°或 55°,55°
70°
55°
55°
70°
70°
40°
思考:等腰三角形一个角为120°,它的另外两个角为___________。
30°, 30°
等腰三角形中角的位置不明确时要分类讨论:
当给出的角是直角或钝角时,它只能是顶角
① 顶角度数+底角度数× 2 =180°
② 0°<底角度数<90°
例2:如图,在△ABC中,AB=AD=DC,
∠BAD=40°,求∠B和∠C的度数。
题型2:两等腰+1角(边化角,知一求二)
探究:如图,已知∠A=15°AB=BC=CD=DE=EF,求∠FEN的度数。
难点:
1.等腰三角形数量多
2.已知角少
突破:标角法
1.找含有已知角的等腰三角形
2.利用知一求二得出其余角
题型2:多等腰+1角(知一求二,各个击破)
题型3:多等腰+一角未知
例3:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD。求△ABC各角的度数。
(用方程)
1、等腰三角形的性质
课堂小结:
说一说,这节课你学到了哪些知识?
2、①1等腰+1角
②两等腰+1角
③多等腰+1角
④多等腰(未知角)
知一求二,分类讨论
找含已知角的等腰三角形
方程思想
作业布置:
学案《等腰三角形的性质1》
谢谢!
