鲁教版(五四制)数学八年级上册 4.3 中心对称(1)课件(共19张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 4.3 中心对称(1)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 257.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 20:37:03 | ||
图片预览






文档简介
(共19张PPT)
第一课时
中心对称
Contents
目录
01
02
03
04
学习目标
实践作图
课堂小结
05
新知探究
巩固练习
1.理解中心对称的概念及其性质;
2.能画出已知图形关于已知点成中心对称的图形。
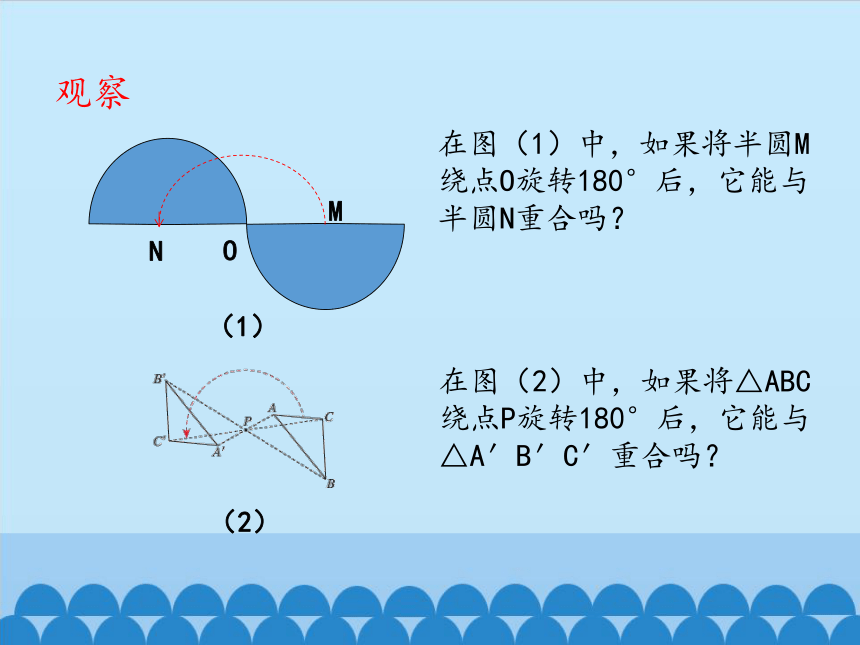
观察
在图(1)中,如果将半圆M绕点O旋转180°后,它能与半圆N重合吗?
在图(2)中,如果将△ABC绕点P旋转180°后,它能与△A′B′C′重合吗?
M
N
O
(1)
(2)
中心对称
在平面内,如果把一个图形绕某个点旋转180°后,它能够与另一个图形重合,那么就说这两个图形关于这个点成中心对称。
这个点叫做对称中心。
两个图形上,经过旋转180°后重合的两个点叫做对应点。
图4-29
O
A
C
C′
A′
B′
B
点A与点A′、点B与点B′、点C与点C′等都是对应点。
如图,△ABC与△A′B′C′关于点O成中心对称,点O是对称中心。
讨论:中心对称与轴对称的区别
性质1 成中心对称的两个图形是全等形。
∵ △ABC与△A′B′C′ 关于点O成中心对称
∴ △ABC≌△A′B′C′
性质2 成中心对称的两个图形中,对应点的连线都经过对称中心,并且被对称中心平分。
∵△ABC与△A′B′C′关于点O成中心对称
∴AA′、BB′、CC′经过点O
且OA=OA′,OB=OB′,OC=OC′
O
A
C
C′
A′
B′
B
解:连接OA,
并延长到A',使OA'=OA,
做一做 已知点A和点O,怎样画出点A关于点O成中心对称的对应点A'。
则A'是所求的点。
如图,D是△ABC的边AC上一点,画出△EFG,使它与△ABC关于点D成中心对称。
B
C
A
D
E
F
G
登高望远
例1 已知四边形ABCD和点O,画出四边形A B C D ,使它与四边形ABCD关于O点成中心对称。
.
C
D
A
B
D
C
O
A
B
解:
1.连接AO并延长到A ,使OA=OA ,得到点A的对称点A ;
2.同样画B、C、D的对称点B 、C 、D ;
3.顺次连接A 、B 、C 、D 各点。
所以,四边形A B C D 就是所求的四边形。
(1)画一个点关于某点(对称中心)的对称点的画法是先连接这个点与对称中心并延长一倍即可。
(2)画一个图形关于某点的对称图形的画法是先画出图形中的几个特殊点(如多边形的顶点、线段的端点,圆的圆心等)关于某点的对称点,然后再顺次连接有关对称点即可。
规律总结
1.已知:下列命题中真命题的个数是( )
①成中心对称的两个图形一定不全等
②成中心对称的两个图形是全等图形
③两个全等的图形一定关于某点成中心对称
A. 0 B. 1 C. 2 D. 3
B
2.
3.
进一步探索
怎样判别两个图形关于某一点成中心对称呢?
如果两个图形的
对应点连成的线
段都经过某一点,
并且被该点平分,
那么这两个图形
一定关于这一点
成中心对称。
1.中心对称的概念及其性质;
本节课我们学习了
2.能画出已知图形关于已知点成中心对称的图形。
注意:轴对称和中心对称的区别和联系。
谢 谢
第一课时
中心对称
Contents
目录
01
02
03
04
学习目标
实践作图
课堂小结
05
新知探究
巩固练习
1.理解中心对称的概念及其性质;
2.能画出已知图形关于已知点成中心对称的图形。
观察
在图(1)中,如果将半圆M绕点O旋转180°后,它能与半圆N重合吗?
在图(2)中,如果将△ABC绕点P旋转180°后,它能与△A′B′C′重合吗?
M
N
O
(1)
(2)
中心对称
在平面内,如果把一个图形绕某个点旋转180°后,它能够与另一个图形重合,那么就说这两个图形关于这个点成中心对称。
这个点叫做对称中心。
两个图形上,经过旋转180°后重合的两个点叫做对应点。
图4-29
O
A
C
C′
A′
B′
B
点A与点A′、点B与点B′、点C与点C′等都是对应点。
如图,△ABC与△A′B′C′关于点O成中心对称,点O是对称中心。
讨论:中心对称与轴对称的区别
性质1 成中心对称的两个图形是全等形。
∵ △ABC与△A′B′C′ 关于点O成中心对称
∴ △ABC≌△A′B′C′
性质2 成中心对称的两个图形中,对应点的连线都经过对称中心,并且被对称中心平分。
∵△ABC与△A′B′C′关于点O成中心对称
∴AA′、BB′、CC′经过点O
且OA=OA′,OB=OB′,OC=OC′
O
A
C
C′
A′
B′
B
解:连接OA,
并延长到A',使OA'=OA,
做一做 已知点A和点O,怎样画出点A关于点O成中心对称的对应点A'。
则A'是所求的点。
如图,D是△ABC的边AC上一点,画出△EFG,使它与△ABC关于点D成中心对称。
B
C
A
D
E
F
G
登高望远
例1 已知四边形ABCD和点O,画出四边形A B C D ,使它与四边形ABCD关于O点成中心对称。
.
C
D
A
B
D
C
O
A
B
解:
1.连接AO并延长到A ,使OA=OA ,得到点A的对称点A ;
2.同样画B、C、D的对称点B 、C 、D ;
3.顺次连接A 、B 、C 、D 各点。
所以,四边形A B C D 就是所求的四边形。
(1)画一个点关于某点(对称中心)的对称点的画法是先连接这个点与对称中心并延长一倍即可。
(2)画一个图形关于某点的对称图形的画法是先画出图形中的几个特殊点(如多边形的顶点、线段的端点,圆的圆心等)关于某点的对称点,然后再顺次连接有关对称点即可。
规律总结
1.已知:下列命题中真命题的个数是( )
①成中心对称的两个图形一定不全等
②成中心对称的两个图形是全等图形
③两个全等的图形一定关于某点成中心对称
A. 0 B. 1 C. 2 D. 3
B
2.
3.
进一步探索
怎样判别两个图形关于某一点成中心对称呢?
如果两个图形的
对应点连成的线
段都经过某一点,
并且被该点平分,
那么这两个图形
一定关于这一点
成中心对称。
1.中心对称的概念及其性质;
本节课我们学习了
2.能画出已知图形关于已知点成中心对称的图形。
注意:轴对称和中心对称的区别和联系。
谢 谢
