冀教版数学八年级上册16.3 角平分线 课件(共18张PPT)
文档属性
| 名称 | 冀教版数学八年级上册16.3 角平分线 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 21:14:07 | ||
图片预览





文档简介
(共18张PPT)
16.3 角平分线
初中数学冀教版八年级上册
1.角平分线的概念
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
C
1
O
B
A
2
在∠AOB中,∵∠1=∠2,∴射线OC是∠AOB的角平分线
复习导入
2、点到直线(或射线)的距离:
P
l
A
B
C
D
图中能表示点P到直线l距离的是 .
过直线(或射线)外一点向这条直线(或射线)作垂线,垂线段的长度即为距离。
pc
注意:垂足、垂直符号
1、角的对称性
∠AOB是轴对称图形,
对称轴是角平分线所在的直线。
O
B
C
A
1
2
探究新知
(1)不借助任何工具,能找到∠AOB的平分线吗?
(2)沿着角平分线对折,角平分线两边的图形能完全重合,这说明了什么?
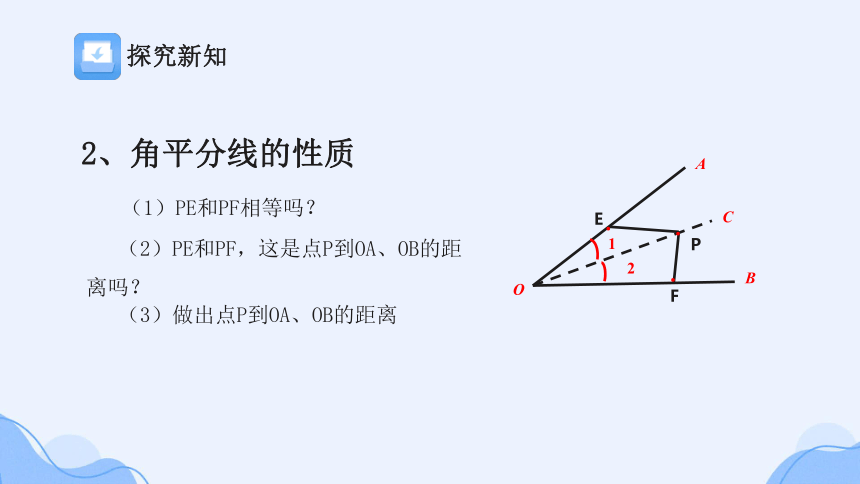
2、角平分线的性质
O
B
C
A
1
2
P
E
F
(1)PE和PF相等吗?
(2)PE和PF,这是点P到OA、OB的距离吗?
探究新知
(3)做出点P到OA、OB的距离
·
·
·
探究新知
2、角平分线的性质
(4)PE、PF在数量上有什么关系?
(5)有哪些方法能证明?
pe=pf
O
B
C
A
1
2
P
E
F
∟
∟
探究新知
O
B
C
A
1
2
P
E
F
∟
∟
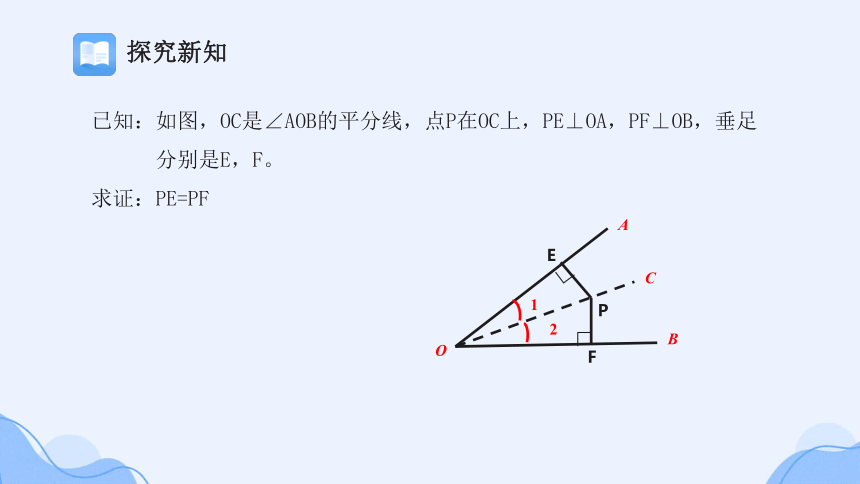
已知:如图,OC是∠AOB的平分线,点P在OC上,PE⊥OA,PF⊥OB,垂足
分别是E,F。
求证:PE=PF
探究新知
角平分线上的点到角的两边的距离相等.
∵OC平分∠AOB,PE⊥OA,PF⊥OB,E、F为垂足,∴ PE=PF
2、角平分线的性质
O
B
C
A
1
2
P
E
F
∟
∟
注意:
1、定理应用时要满足3个条件:角平分线;点在角平分线上;距离(即点与垂足之间的垂线段的长)
2、证明线段相等可以用三角形全等、线段垂直平分线性质定理,还可以用角平分线的性质。
练一练
1、 下面四个图中,点P都在∠AOB的平分线上,则图形( )中,PD=PE.
【思路点拨】利用角平分线的性质时,非常重要的条件是PD和PE是到角两边的距离(即垂线段的长)。
d
2、如图,△ABC中,∠C=900,AD是∠BAC的平分线, DE⊥AB于E,BC=8,BD=5,求DE的长。
A
C
B
┌
┌
D
E
3、如图,△ABC中,∠A=900,BD平分∠ABC,AD=3cm,BC
=8cm,试求△BCD的面积。
B
A
C
┌
D
4、如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D。学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远。请你帮忙找到灯柱的位置P,并说明理由。
A
O
B
C
D
·
·
如图,直线l1、l2、l3表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的位置有几处?请在图中标出来。
l1
l2
l3
思考:
课堂总结
本节课你有哪些收获?
布置作业
1、必做题:P122 习题A组 1、2、3
2、选做题: P123 习题B组 1、2
再 见!
16.3 角平分线
初中数学冀教版八年级上册
1.角平分线的概念
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
C
1
O
B
A
2
在∠AOB中,∵∠1=∠2,∴射线OC是∠AOB的角平分线
复习导入
2、点到直线(或射线)的距离:
P
l
A
B
C
D
图中能表示点P到直线l距离的是 .
过直线(或射线)外一点向这条直线(或射线)作垂线,垂线段的长度即为距离。
pc
注意:垂足、垂直符号
1、角的对称性
∠AOB是轴对称图形,
对称轴是角平分线所在的直线。
O
B
C
A
1
2
探究新知
(1)不借助任何工具,能找到∠AOB的平分线吗?
(2)沿着角平分线对折,角平分线两边的图形能完全重合,这说明了什么?
2、角平分线的性质
O
B
C
A
1
2
P
E
F
(1)PE和PF相等吗?
(2)PE和PF,这是点P到OA、OB的距离吗?
探究新知
(3)做出点P到OA、OB的距离
·
·
·
探究新知
2、角平分线的性质
(4)PE、PF在数量上有什么关系?
(5)有哪些方法能证明?
pe=pf
O
B
C
A
1
2
P
E
F
∟
∟
探究新知
O
B
C
A
1
2
P
E
F
∟
∟
已知:如图,OC是∠AOB的平分线,点P在OC上,PE⊥OA,PF⊥OB,垂足
分别是E,F。
求证:PE=PF
探究新知
角平分线上的点到角的两边的距离相等.
∵OC平分∠AOB,PE⊥OA,PF⊥OB,E、F为垂足,∴ PE=PF
2、角平分线的性质
O
B
C
A
1
2
P
E
F
∟
∟
注意:
1、定理应用时要满足3个条件:角平分线;点在角平分线上;距离(即点与垂足之间的垂线段的长)
2、证明线段相等可以用三角形全等、线段垂直平分线性质定理,还可以用角平分线的性质。
练一练
1、 下面四个图中,点P都在∠AOB的平分线上,则图形( )中,PD=PE.
【思路点拨】利用角平分线的性质时,非常重要的条件是PD和PE是到角两边的距离(即垂线段的长)。
d
2、如图,△ABC中,∠C=900,AD是∠BAC的平分线, DE⊥AB于E,BC=8,BD=5,求DE的长。
A
C
B
┌
┌
D
E
3、如图,△ABC中,∠A=900,BD平分∠ABC,AD=3cm,BC
=8cm,试求△BCD的面积。
B
A
C
┌
D
4、如图,校园有两条路OA、OB,在交叉口附近有两块宣传牌C、D。学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远。请你帮忙找到灯柱的位置P,并说明理由。
A
O
B
C
D
·
·
如图,直线l1、l2、l3表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的位置有几处?请在图中标出来。
l1
l2
l3
思考:
课堂总结
本节课你有哪些收获?
布置作业
1、必做题:P122 习题A组 1、2、3
2、选做题: P123 习题B组 1、2
再 见!
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
