冀教版数学八年级上册17.3勾股定理 课件(共30张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.3勾股定理 课件(共30张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
美丽又神奇的勾股树
美丽又神奇的勾股树
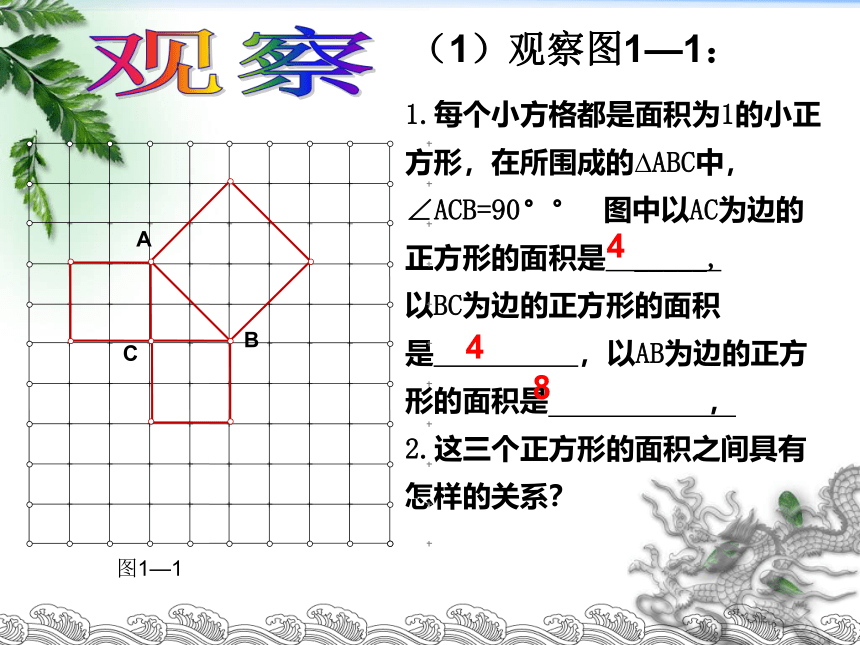
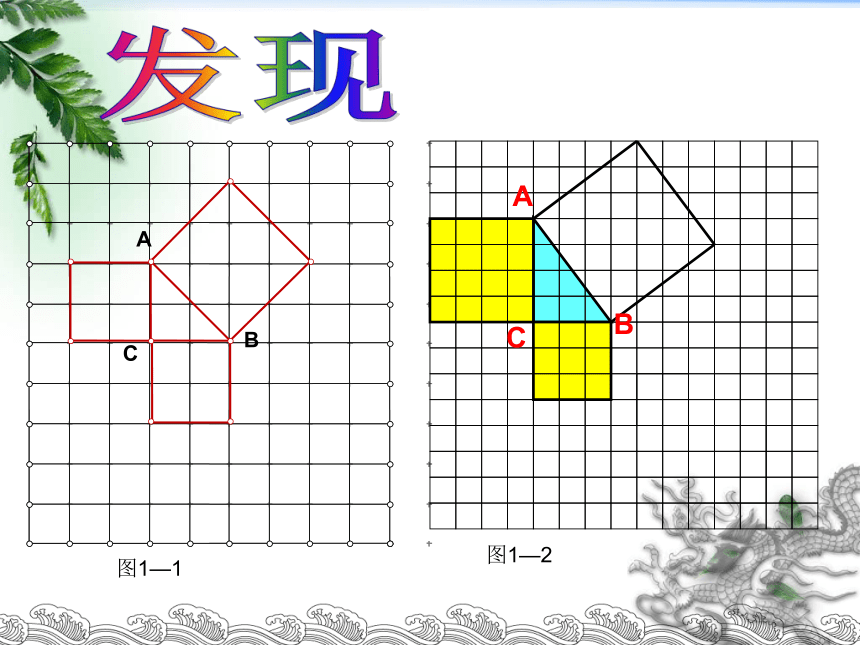
(1)观察图1—1:
1.每个小方格都是面积为1的小正方形,在所围成的 ABC中,∠ACB=90 图中以AC为边的正方形的面积是 _____,
以BC为边的正方形的面积是 ,以AB为边的正方形的面积是 ,
2.这三个正方形的面积之间具有怎样的关系?
8
4
4
图1—1
A
B
C
讨论交流
如何计算以AB为边的正方形的面积?
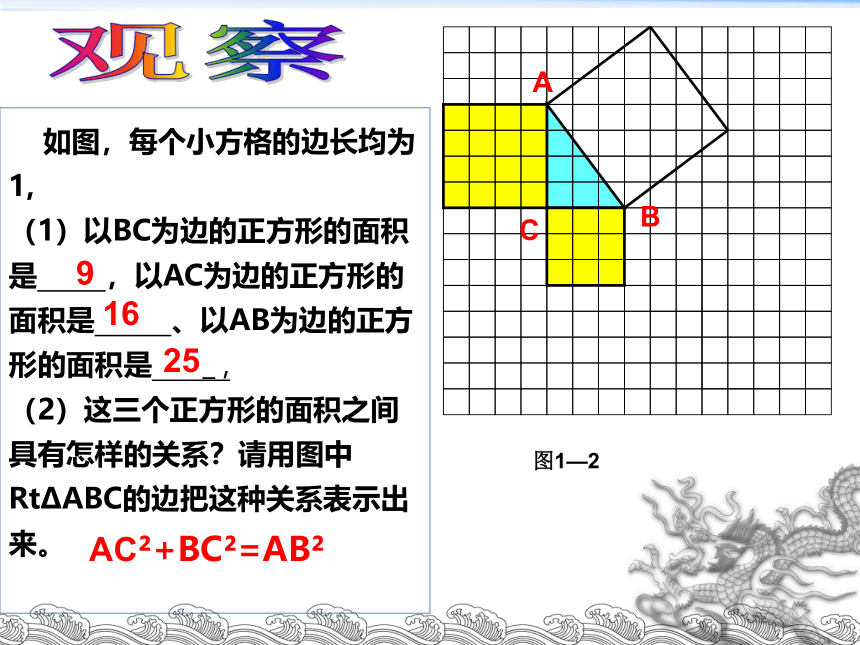
2.如图,每个小方格的边长均为1,
(1)以BC为边的正方形的面积是 ,以AC为边的正方形的面积是 、以AB为边的正方形的面积是 _,
(2)这三个正方形的面积之间具有怎样的关系?请用图中Rt ABC的边把这种关系表示出来。
9
16
25
A
B
C
AC +BC =AB
图1—2
A
B
C
C
A
B
C
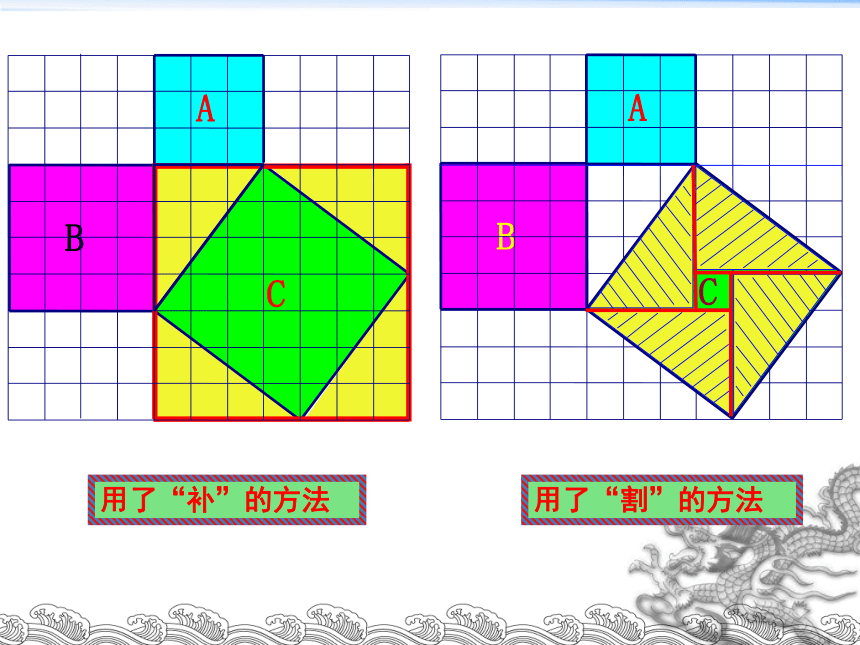
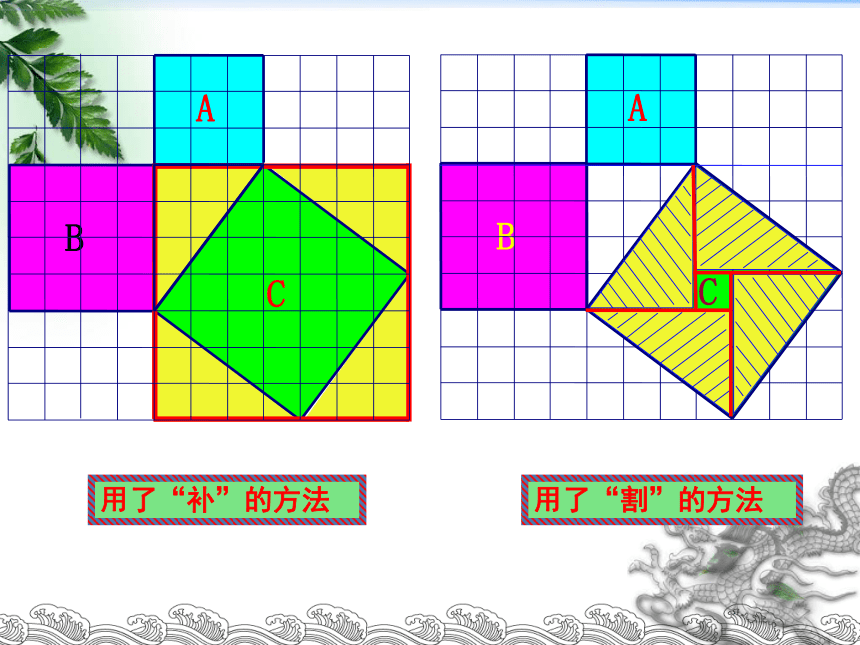
用了“割”的方法
用了“补”的方法
如图,每个小方格的边长均为1,
(1)以BC为边的正方形的面积是 ,以AC为边的正方形的面积是 、以AB为边的正方形的面积是 _,
(2)这三个正方形的面积之间具有怎样的关系?请用图中Rt ABC的边把这种关系表示出来。
9
16
25
A
B
C
AC +BC =AB
图1—2
A
B
C
C
A
B
C
用了“割”的方法
用了“补”的方法
图1—1
A
B
C
A
B
C
图1—2
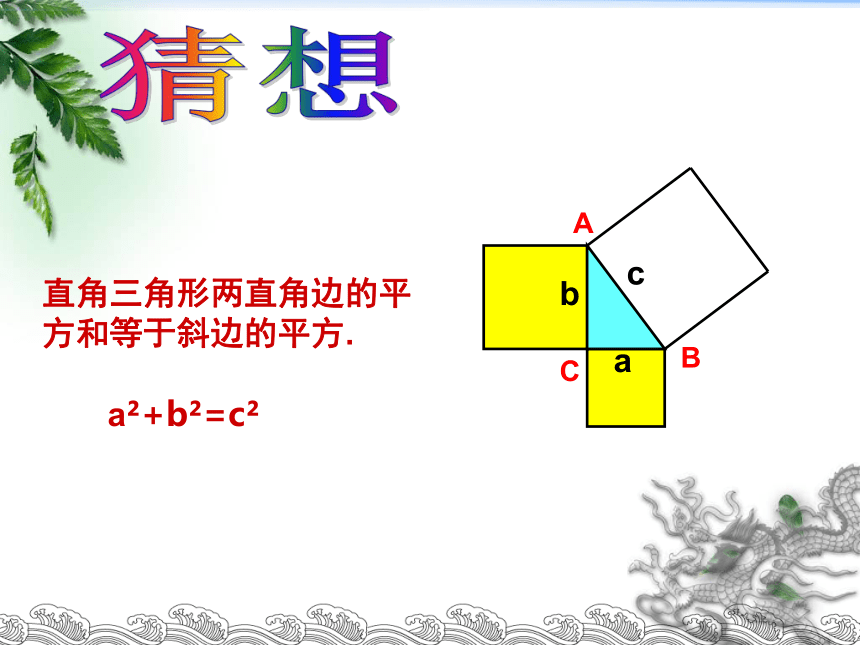
直角三角形两直角边的平方和等于斜边的平方.
a +b =c
A
C
B
a
b
c
1. 用你手中的四个全等直角三角形拼成一个大正方形(内部可以中空)。
2. 你能把拼出的大正方形的面积表示出来吗?能用几种方式?
3. 你能利用面积之间的关系推导出a +b =c 吗?若能,写出推导过程。
b
a
c
利用右图证明a2+b2=c2?
可得: a2 + b2 = c2
追寻前人的足迹
2002年国际数学家大会会标
b
a
b
a
b
a
b
a
b
a
c
面积关系是认识和发现图形性质的一条重要渠道。
勾
股
C
如果直角三角形两直角边分别为a、b,斜边为c, 那么:
即:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾股定理
美丽又神奇的勾股树
a
b
c
C
A
B
已知:在Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c = 10,b = 8,则a= ;
③若c = 25 ,a = 24 ,则b= .
结论变形
13
6
7
通过这节课的学习,你学到什么知识?你有哪些方面的感悟
当堂检测
5.根据图4及提示证明勾股定理.
【提示】:三个三角形的面积和 = 一个梯形的面积.
图3
图4
若一个直角三角形的三边长分别为8,15, x,则x= .
感 悟
分类讨论是一种重要的解题方法.
要养成用数学的思维去解读世界的习惯。
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
教师寄语
美丽的勾股树
神奇的
A
B
C
a
c
b
如果直角三角形的两直角边长分别为a、b,斜边为c ,那么:
a2+b2=c2.
证法欣赏
在印度、阿拉伯世界和欧洲出现的一种拼图证明.
拓展提高
图1
图2
一般情况探究
每个小正方形方格的边长都是1 ,则每个小正方形的面积是1平方单位。
B
3
2
思考:
以AC为一边的正方形面积AC2是 ,
以BC为一边的正方形面积BC2是 ,
以AB为一边的正方形面积AB2是 ,
4
9
13
A
C
3
2
3
2
3
2
3
2
3
3
3
3
25
3
3
3
3
—3×4=13
说出你的发现:
b
a
b
a
b
a
b
a
c
c
c
c
可得: a2 + b2 = c2
利用下图证明a2+b2=c2?
追寻前人的足迹
美丽又神奇的勾股树
美丽又神奇的勾股树
(1)观察图1—1:
1.每个小方格都是面积为1的小正方形,在所围成的 ABC中,∠ACB=90 图中以AC为边的正方形的面积是 _____,
以BC为边的正方形的面积是 ,以AB为边的正方形的面积是 ,
2.这三个正方形的面积之间具有怎样的关系?
8
4
4
图1—1
A
B
C
讨论交流
如何计算以AB为边的正方形的面积?
2.如图,每个小方格的边长均为1,
(1)以BC为边的正方形的面积是 ,以AC为边的正方形的面积是 、以AB为边的正方形的面积是 _,
(2)这三个正方形的面积之间具有怎样的关系?请用图中Rt ABC的边把这种关系表示出来。
9
16
25
A
B
C
AC +BC =AB
图1—2
A
B
C
C
A
B
C
用了“割”的方法
用了“补”的方法
如图,每个小方格的边长均为1,
(1)以BC为边的正方形的面积是 ,以AC为边的正方形的面积是 、以AB为边的正方形的面积是 _,
(2)这三个正方形的面积之间具有怎样的关系?请用图中Rt ABC的边把这种关系表示出来。
9
16
25
A
B
C
AC +BC =AB
图1—2
A
B
C
C
A
B
C
用了“割”的方法
用了“补”的方法
图1—1
A
B
C
A
B
C
图1—2
直角三角形两直角边的平方和等于斜边的平方.
a +b =c
A
C
B
a
b
c
1. 用你手中的四个全等直角三角形拼成一个大正方形(内部可以中空)。
2. 你能把拼出的大正方形的面积表示出来吗?能用几种方式?
3. 你能利用面积之间的关系推导出a +b =c 吗?若能,写出推导过程。
b
a
c
利用右图证明a2+b2=c2?
可得: a2 + b2 = c2
追寻前人的足迹
2002年国际数学家大会会标
b
a
b
a
b
a
b
a
b
a
c
面积关系是认识和发现图形性质的一条重要渠道。
勾
股
C
如果直角三角形两直角边分别为a、b,斜边为c, 那么:
即:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾股定理
美丽又神奇的勾股树
a
b
c
C
A
B
已知:在Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c = 10,b = 8,则a= ;
③若c = 25 ,a = 24 ,则b= .
结论变形
13
6
7
通过这节课的学习,你学到什么知识?你有哪些方面的感悟
当堂检测
5.根据图4及提示证明勾股定理.
【提示】:三个三角形的面积和 = 一个梯形的面积.
图3
图4
若一个直角三角形的三边长分别为8,15, x,则x= .
感 悟
分类讨论是一种重要的解题方法.
要养成用数学的思维去解读世界的习惯。
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步。
其实数学在我们的生活中无处不在, 只要你是个有心人,就一定会发现在我们的身边,我们的眼前, 还有很多象 “勾股定理”那样的知识等待我们去探索,等待我们去发现……
教师寄语
美丽的勾股树
神奇的
A
B
C
a
c
b
如果直角三角形的两直角边长分别为a、b,斜边为c ,那么:
a2+b2=c2.
证法欣赏
在印度、阿拉伯世界和欧洲出现的一种拼图证明.
拓展提高
图1
图2
一般情况探究
每个小正方形方格的边长都是1 ,则每个小正方形的面积是1平方单位。
B
3
2
思考:
以AC为一边的正方形面积AC2是 ,
以BC为一边的正方形面积BC2是 ,
以AB为一边的正方形面积AB2是 ,
4
9
13
A
C
3
2
3
2
3
2
3
2
3
3
3
3
25
3
3
3
3
—3×4=13
说出你的发现:
b
a
b
a
b
a
b
a
c
c
c
c
可得: a2 + b2 = c2
利用下图证明a2+b2=c2?
追寻前人的足迹
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
