冀教版数学八年级上册16.2 线段的垂直平分线(3) 课件(共13张PPT)
文档属性
| 名称 | 冀教版数学八年级上册16.2 线段的垂直平分线(3) 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 184.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-02 21:17:57 | ||
图片预览





文档简介
(共13张PPT)
线段的垂直平分线
第三课时
〔解析〕 因为向三个村庄分别送水,三条输水管长度相同,所以水泵站应在AB,BC的中垂线的交点处.
说明:那么如何用尺规作图的方法作出线段的中垂线呢
问题思考
如图所示,点A,B,C表示三个村庄,现要建一座深井水泵站,向三个村庄分别送水,为使三条输水管长度相同,水泵站应建在何处 请画示意图,并说明理由.
学习新知
活动一:作线段的垂直平分线
要作出线段的垂直平分线,根据垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上,那么我们必须找到两个与线段两个端点距离相等的点,这样才能确定已知线段的垂直平分线.
我们曾用折纸的方法折出过线段的垂直平分线,现在我们学习了线段的垂直平分线的性质和判定,能否用尺规作图的方法作出已知线段的垂直平分线呢
如图所示,已知线段AB.
求作:线段AB的垂直平分线.
〔解析〕 由线段垂直平分线性质定理的逆定理可知,只要作出到这条线段端点距离相等的两点,连接这两个点,即得所求作的直线.
作法:如图所示.
(1)分别以点A和点B为圆心,a( ) 为半径,在线段AB的两侧画弧,分别相交于点C,D.
(2)连接CD.
直线CD即为所求.
C
D
我们曾用刻度尺找线段的中点,当我们学习了线段的垂直平分线的作法时,一旦垂直平分线作出,线段与线段的垂直平分线的交点就是线段的中点,所以我们也用这种方法找线段的中点.
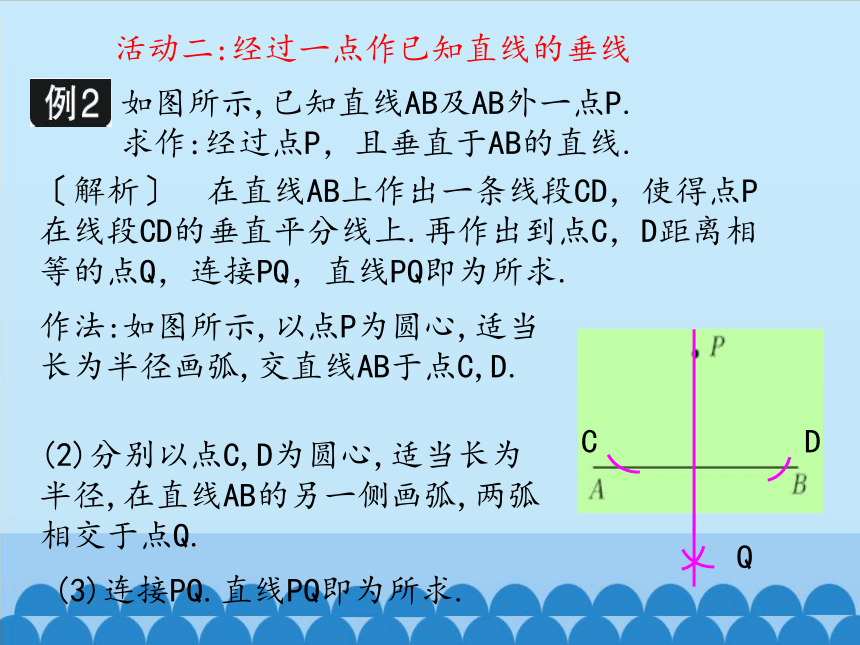
活动二:经过一点作已知直线的垂线
如图所示,已知直线AB及AB外一点P.
求作:经过点P,且垂直于AB的直线.
〔解析〕 在直线AB上作出一条线段CD,使得点P在线段CD的垂直平分线上.再作出到点C,D距离相等的点Q,连接PQ,直线PQ即为所求.
作法:如图所示,以点P为圆心,适当长为半径画弧,交直线AB于点C,D.
(3)连接PQ.直线PQ即为所求.
(2)分别以点C,D为圆心,适当长为半径,在直线AB的另一侧画弧,两弧相交于点Q.
C
D
Q
2.过一点作已知直线的垂线,由于已知点与直线可以有两种不同的位置关系:①点在直线外;
②点在直线上,因此同学们在作图时要掌握这两种方法的区别.
1.根据线段垂直平分线的性质定理的逆定理,只要找到两个到线段两端距离相等的点,那么过这两点就可以作出线段的垂直平分线.
课堂小结
检测反馈
1.利用尺规作线段MN的垂直平分线时,设以M,N为圆心所画弧的半径分别为RM,RN,则下列说法正确的是( )
A.RM与RN不一定相等,但必须RM > MN,RN > MN
B.RM=RN> MN
C.RM>RN> MN
D.RM=RN= MN
解析:根据作已知线段的垂直平分线的画法即可知B正确.故选B.
B
2.如图(1)所示,在河岸l的同侧有A,B两村,要在河边修一水泵站P,使水送到A,B两村所用的水管最短(两村不共用水管).另在河边修一码头Q,使其到A,B两村的距离相等,试画出P,Q所在的位置.
解析:点P为点A关于直线l的对称点和点B的连线与l的交点,点Q为线段AB垂直平分线与l的交点.
解:如图(2)所示,作点A关于直线l的对称点A',连接A'B交直线l于点P.连接AB,作线段AB的垂直平分线,交直线l于点Q.P,Q两点对应的位置就是所求的位置.
3.如图所示,请你在下列各图中,过点P画出射线AB或线段AB的垂线.
解:如图所示.
4.如图所示,已知钝角∠AOB,点D在射线OB上.
(1)画直线DE⊥OB;
(2)画直线DF⊥OA,垂足为F.
解:(1)如图所示. (2)如图所示.
5.如图所示,已知ΔABC中,AB=2,BC=4.
(1)画出ΔABC的高AD和CE;
(2)若AD= ,求CE的长.
解:(1)如图所示.
6.画图并回答问题.
(1)过点P画OA的垂线交OC于点B;
(2)画点P到OB的垂线段PM;
(3)指出上述作图中哪条线段的长度表示P点到OB的距离;
(4)比较PM与OP的大小,并说明理由.
解:(1)如图所示.
(2)如图所示.
(3)PM的长度表示P点到OB的距离.
(4)PM谢 谢
线段的垂直平分线
第三课时
〔解析〕 因为向三个村庄分别送水,三条输水管长度相同,所以水泵站应在AB,BC的中垂线的交点处.
说明:那么如何用尺规作图的方法作出线段的中垂线呢
问题思考
如图所示,点A,B,C表示三个村庄,现要建一座深井水泵站,向三个村庄分别送水,为使三条输水管长度相同,水泵站应建在何处 请画示意图,并说明理由.
学习新知
活动一:作线段的垂直平分线
要作出线段的垂直平分线,根据垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上,那么我们必须找到两个与线段两个端点距离相等的点,这样才能确定已知线段的垂直平分线.
我们曾用折纸的方法折出过线段的垂直平分线,现在我们学习了线段的垂直平分线的性质和判定,能否用尺规作图的方法作出已知线段的垂直平分线呢
如图所示,已知线段AB.
求作:线段AB的垂直平分线.
〔解析〕 由线段垂直平分线性质定理的逆定理可知,只要作出到这条线段端点距离相等的两点,连接这两个点,即得所求作的直线.
作法:如图所示.
(1)分别以点A和点B为圆心,a( ) 为半径,在线段AB的两侧画弧,分别相交于点C,D.
(2)连接CD.
直线CD即为所求.
C
D
我们曾用刻度尺找线段的中点,当我们学习了线段的垂直平分线的作法时,一旦垂直平分线作出,线段与线段的垂直平分线的交点就是线段的中点,所以我们也用这种方法找线段的中点.
活动二:经过一点作已知直线的垂线
如图所示,已知直线AB及AB外一点P.
求作:经过点P,且垂直于AB的直线.
〔解析〕 在直线AB上作出一条线段CD,使得点P在线段CD的垂直平分线上.再作出到点C,D距离相等的点Q,连接PQ,直线PQ即为所求.
作法:如图所示,以点P为圆心,适当长为半径画弧,交直线AB于点C,D.
(3)连接PQ.直线PQ即为所求.
(2)分别以点C,D为圆心,适当长为半径,在直线AB的另一侧画弧,两弧相交于点Q.
C
D
Q
2.过一点作已知直线的垂线,由于已知点与直线可以有两种不同的位置关系:①点在直线外;
②点在直线上,因此同学们在作图时要掌握这两种方法的区别.
1.根据线段垂直平分线的性质定理的逆定理,只要找到两个到线段两端距离相等的点,那么过这两点就可以作出线段的垂直平分线.
课堂小结
检测反馈
1.利用尺规作线段MN的垂直平分线时,设以M,N为圆心所画弧的半径分别为RM,RN,则下列说法正确的是( )
A.RM与RN不一定相等,但必须RM > MN,RN > MN
B.RM=RN> MN
C.RM>RN> MN
D.RM=RN= MN
解析:根据作已知线段的垂直平分线的画法即可知B正确.故选B.
B
2.如图(1)所示,在河岸l的同侧有A,B两村,要在河边修一水泵站P,使水送到A,B两村所用的水管最短(两村不共用水管).另在河边修一码头Q,使其到A,B两村的距离相等,试画出P,Q所在的位置.
解析:点P为点A关于直线l的对称点和点B的连线与l的交点,点Q为线段AB垂直平分线与l的交点.
解:如图(2)所示,作点A关于直线l的对称点A',连接A'B交直线l于点P.连接AB,作线段AB的垂直平分线,交直线l于点Q.P,Q两点对应的位置就是所求的位置.
3.如图所示,请你在下列各图中,过点P画出射线AB或线段AB的垂线.
解:如图所示.
4.如图所示,已知钝角∠AOB,点D在射线OB上.
(1)画直线DE⊥OB;
(2)画直线DF⊥OA,垂足为F.
解:(1)如图所示. (2)如图所示.
5.如图所示,已知ΔABC中,AB=2,BC=4.
(1)画出ΔABC的高AD和CE;
(2)若AD= ,求CE的长.
解:(1)如图所示.
6.画图并回答问题.
(1)过点P画OA的垂线交OC于点B;
(2)画点P到OB的垂线段PM;
(3)指出上述作图中哪条线段的长度表示P点到OB的距离;
(4)比较PM与OP的大小,并说明理由.
解:(1)如图所示.
(2)如图所示.
(3)PM的长度表示P点到OB的距离.
(4)PM
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
