4.2力的分解 课件 (29张PPT)
文档属性
| 名称 | 4.2力的分解 课件 (29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-03 10:39:07 | ||
图片预览





文档简介
4.2
力的分解
学习目标:
1.理解力的分解和分力的概念。
2.理解力的分解是力的合成的逆运算,会用平行四边形定则求分力。(重点)
3.掌握力的正交分解的方法。(重点)
4.会用力的分解分析生产和生活中的实际问题。(难点)
物体受到多个力的作用时,可用一个力来等效替代。若物体受到某一个力的作用,是否也可以用几个力来等效替代?
一、力的分解
(1)定义:
求一个已知力的分力叫做力的分解,是力的合成的逆运算。
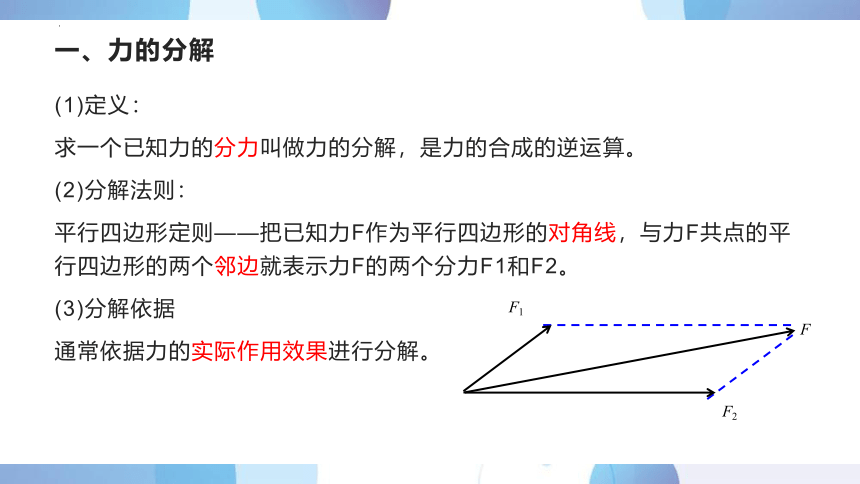
(2)分解法则:
平行四边形定则——把已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1和F2。
(3)分解依据
通常依据力的实际作用效果进行分解。
F
F1
F2
思考:
1.一个力只能分解为一组分力。( )
2.力的分解遵循平行四边形定则。( )
3.某个分力的大小不可能大于合力。( )
4.已知一个力,把它分解为两个力,如果没有其他条件限制,可分解为多少对分力?
X
√
X
F
F1
F2
o
合力的合成
有唯一解
F
合力的分解
有无数个解
F1
F2
F1
F2
F1
F2
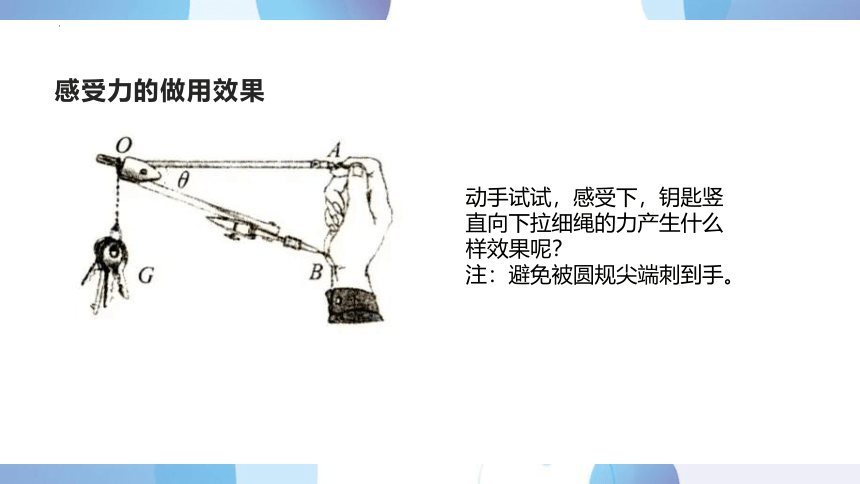
感受力的做用效果
动手试试,感受下,钥匙竖直向下拉细绳的力产生什么样效果呢?
注:避免被圆规尖端刺到手。
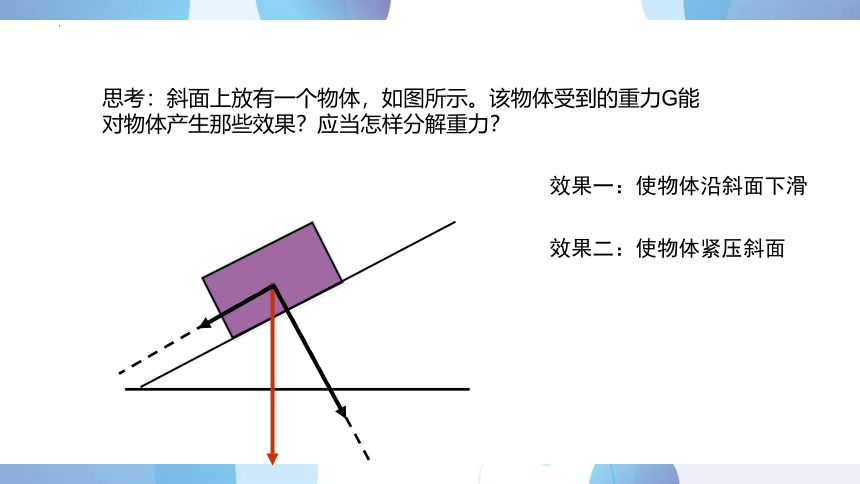
思考:斜面上放有一个物体,如图所示。该物体受到的重力G能对物体产生那些效果?应当怎样分解重力?
效果一:使物体沿斜面下滑
效果二:使物体紧压斜面
F
G
F
a
b
F
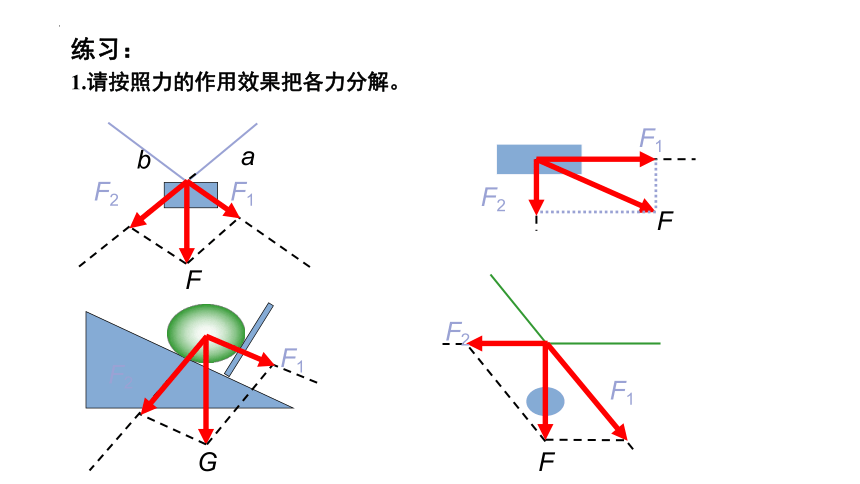
练习:
1.请按照力的作用效果把各力分解。
F1
F1
F1
F1
F2
F2
F2
F2
2.如图所示,把光滑斜面上的物体所受重力mg分解为F1、F2两个力.图中FN为斜面对物体的支持力,则下列说法正确的是 ( )
A.F1是斜面作用在物体上使物体下滑的力
B.物体受到mg、FN、F1、F2共四个力的作用
C.F2是物体对斜面的压力
D.力FN、F1、F2这三个力的作用效果与mg、FN这两个力的作用效果相同
D
力的分解总结:
(2)按实际效果分解的几个实例:
{5940675A-B579-460E-94D1-54222C63F5DA}实例
分析
(1)拉力F的效果:①使物体沿水平地面前进(或趋势)②向上提物体(2)两个分力:水平向前的力F1和竖直向上的力F2。F1=Fcos α,F2=Fsin α
{5940675A-B579-460E-94D1-54222C63F5DA}
(1)重力的两个效果: ①使物体具有沿斜面下滑(或趋势)的分力F1②使物体压紧斜面的分力F2
(2)分力大小:F1=mgsin α,F2=mgcos α
(1)重力的两个效果:①使球压紧板的分力F1②使球压紧斜面的分力F2
(2)分力大小:F1=mgtan α,F2=
{5940675A-B579-460E-94D1-54222C63F5DA}
(1)重力的两个效果:①使球压紧竖直墙壁的分力F1②使球拉紧悬线的分力F2
(2)分力大小:F1=mgtan α,F2=
(1)重力的两个效果:①对OA的拉力F1②对OB的拉力F2
(2)分力大小:F1=mgtan α,F2=
F
合力的分解
有无数个解
F1
F2
F1
F2
F1
F2
在给定的条件下,合力可以有几种分解呢?
无数?
一个?
无解?
两个、三个?
力分解情况的讨论(拓展):
力的分解会出现有解或无解,简单地说,就是代表合力的对角线与给定的代表分力的有向线段是否构成平行四边形(或三角形).若可以构成平行四边形(或三角形),说明合力可以分解成给定分力,即有解;若不能,则无解.具体讨论如下:
①已知两个分力的方向:
②已知一个分力的大小和方向:
③已知两个分力的大小(同一平面内:
④已知合力的大小和方向以及一个分力的大小和另一个分力的方向:
唯一解
两解
唯一解
唯一解
无解
两解
唯一解
二、力的正交分解
在许多的情况下,为了计算方便,可把一个力分解为两个互相垂直的分力,这种分解方法称为力的正交分解。
1.公式:Fx= Fcosθ ,Fy=Fsinθ
2.适用:正交分解适用于各种矢量运算
3.优点:将矢量运算转化成坐标轴方向上的 运算
注:不一定水平竖直,两个方向必须垂直
正交分解的基本步骤
(1)建立坐标系
以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力落在坐标轴上。
(2)正交分解各力
将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示。
(3)分别求出x轴、y轴上各分力的合力,即:
Fx=F1x+F2x+…
Fy=F1y+F2y+…
(4)求共点力的合力
合力大小F= ,合力的方向与x轴的夹角为α,
则tan α= ,即α=arctan .
F
Fx
Fy
例1、某人用力F=20 N 斜向上30°的力拉物体, 请利用正交分解法求水平和竖直两个方向上的分力。
两个分力的大小为:
q
y
x
两个方向的合力的大小为:
120o
120o
120o
x
y
F1=20 N
F2=30 N
F3=40 N
F2x
F2y
F3y
F3x
例2、三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力。
练习:1.如图所示,对称晾挂在光滑等腰三角形衣架上的衣服质量为M,衣架顶角为120°,重力加速度为g,则衣架右侧对衣服的作用力大小为( )
A. Mg B. Mg
C. Mg D.Mg
B
解析:以衣服为研究对象,受力分析如图所示,由几何关系得F与竖直方向的夹角为30°,由共点力的平衡条件可得,2Fcos 30°=Mg,解得F= Mg,故选项B正确。
三、力的分解的应用
为了行车方便和安全,高大的桥往往有很长的引桥。
探讨1:在引桥上,汽车重力有什么作用效果?
【提示】汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行。
【提示】高大的桥建造很长的引桥可以减小汽车重力沿斜面向下的分力,使行车更安全。
探讨2:从力的分解的角度分析,引桥很长有什么好处?
思考:用一根结实的长绳,一棵大树,一位同学就可以将陷入泥沼的小汽车拉出.这是真的吗?
现实生活中利用力的合成与分解求解的实例相当多,如斜拉索公路桥、用斧子劈木桩,另外,还有汽车换轮胎时用的剪式千斤顶、砖石结构的拱桥、工人向车上装货物时使用较长的木板、将立交桥的匝道建造得很长等。
课堂小结
THANKS
力的分解
学习目标:
1.理解力的分解和分力的概念。
2.理解力的分解是力的合成的逆运算,会用平行四边形定则求分力。(重点)
3.掌握力的正交分解的方法。(重点)
4.会用力的分解分析生产和生活中的实际问题。(难点)
物体受到多个力的作用时,可用一个力来等效替代。若物体受到某一个力的作用,是否也可以用几个力来等效替代?
一、力的分解
(1)定义:
求一个已知力的分力叫做力的分解,是力的合成的逆运算。
(2)分解法则:
平行四边形定则——把已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1和F2。
(3)分解依据
通常依据力的实际作用效果进行分解。
F
F1
F2
思考:
1.一个力只能分解为一组分力。( )
2.力的分解遵循平行四边形定则。( )
3.某个分力的大小不可能大于合力。( )
4.已知一个力,把它分解为两个力,如果没有其他条件限制,可分解为多少对分力?
X
√
X
F
F1
F2
o
合力的合成
有唯一解
F
合力的分解
有无数个解
F1
F2
F1
F2
F1
F2
感受力的做用效果
动手试试,感受下,钥匙竖直向下拉细绳的力产生什么样效果呢?
注:避免被圆规尖端刺到手。
思考:斜面上放有一个物体,如图所示。该物体受到的重力G能对物体产生那些效果?应当怎样分解重力?
效果一:使物体沿斜面下滑
效果二:使物体紧压斜面
F
G
F
a
b
F
练习:
1.请按照力的作用效果把各力分解。
F1
F1
F1
F1
F2
F2
F2
F2
2.如图所示,把光滑斜面上的物体所受重力mg分解为F1、F2两个力.图中FN为斜面对物体的支持力,则下列说法正确的是 ( )
A.F1是斜面作用在物体上使物体下滑的力
B.物体受到mg、FN、F1、F2共四个力的作用
C.F2是物体对斜面的压力
D.力FN、F1、F2这三个力的作用效果与mg、FN这两个力的作用效果相同
D
力的分解总结:
(2)按实际效果分解的几个实例:
{5940675A-B579-460E-94D1-54222C63F5DA}实例
分析
(1)拉力F的效果:①使物体沿水平地面前进(或趋势)②向上提物体(2)两个分力:水平向前的力F1和竖直向上的力F2。F1=Fcos α,F2=Fsin α
{5940675A-B579-460E-94D1-54222C63F5DA}
(1)重力的两个效果: ①使物体具有沿斜面下滑(或趋势)的分力F1②使物体压紧斜面的分力F2
(2)分力大小:F1=mgsin α,F2=mgcos α
(1)重力的两个效果:①使球压紧板的分力F1②使球压紧斜面的分力F2
(2)分力大小:F1=mgtan α,F2=
{5940675A-B579-460E-94D1-54222C63F5DA}
(1)重力的两个效果:①使球压紧竖直墙壁的分力F1②使球拉紧悬线的分力F2
(2)分力大小:F1=mgtan α,F2=
(1)重力的两个效果:①对OA的拉力F1②对OB的拉力F2
(2)分力大小:F1=mgtan α,F2=
F
合力的分解
有无数个解
F1
F2
F1
F2
F1
F2
在给定的条件下,合力可以有几种分解呢?
无数?
一个?
无解?
两个、三个?
力分解情况的讨论(拓展):
力的分解会出现有解或无解,简单地说,就是代表合力的对角线与给定的代表分力的有向线段是否构成平行四边形(或三角形).若可以构成平行四边形(或三角形),说明合力可以分解成给定分力,即有解;若不能,则无解.具体讨论如下:
①已知两个分力的方向:
②已知一个分力的大小和方向:
③已知两个分力的大小(同一平面内:
④已知合力的大小和方向以及一个分力的大小和另一个分力的方向:
唯一解
两解
唯一解
唯一解
无解
两解
唯一解
二、力的正交分解
在许多的情况下,为了计算方便,可把一个力分解为两个互相垂直的分力,这种分解方法称为力的正交分解。
1.公式:Fx= Fcosθ ,Fy=Fsinθ
2.适用:正交分解适用于各种矢量运算
3.优点:将矢量运算转化成坐标轴方向上的 运算
注:不一定水平竖直,两个方向必须垂直
正交分解的基本步骤
(1)建立坐标系
以共点力的作用点为坐标原点,直角坐标系x轴和y轴的选择应使尽量多的力落在坐标轴上。
(2)正交分解各力
将每一个不在坐标轴上的力分解到x轴和y轴上,并求出各分力的大小,如图所示。
(3)分别求出x轴、y轴上各分力的合力,即:
Fx=F1x+F2x+…
Fy=F1y+F2y+…
(4)求共点力的合力
合力大小F= ,合力的方向与x轴的夹角为α,
则tan α= ,即α=arctan .
F
Fx
Fy
例1、某人用力F=20 N 斜向上30°的力拉物体, 请利用正交分解法求水平和竖直两个方向上的分力。
两个分力的大小为:
q
y
x
两个方向的合力的大小为:
120o
120o
120o
x
y
F1=20 N
F2=30 N
F3=40 N
F2x
F2y
F3y
F3x
例2、三个共点力F1=20 N、F2=30 N、F3=40 N,它们相互间的夹角为120o,求它们的合力。
练习:1.如图所示,对称晾挂在光滑等腰三角形衣架上的衣服质量为M,衣架顶角为120°,重力加速度为g,则衣架右侧对衣服的作用力大小为( )
A. Mg B. Mg
C. Mg D.Mg
B
解析:以衣服为研究对象,受力分析如图所示,由几何关系得F与竖直方向的夹角为30°,由共点力的平衡条件可得,2Fcos 30°=Mg,解得F= Mg,故选项B正确。
三、力的分解的应用
为了行车方便和安全,高大的桥往往有很长的引桥。
探讨1:在引桥上,汽车重力有什么作用效果?
【提示】汽车重力的两个作用效果是垂直桥面向下使汽车压斜面和沿桥面向下使汽车下滑或阻碍汽车上行。
【提示】高大的桥建造很长的引桥可以减小汽车重力沿斜面向下的分力,使行车更安全。
探讨2:从力的分解的角度分析,引桥很长有什么好处?
思考:用一根结实的长绳,一棵大树,一位同学就可以将陷入泥沼的小汽车拉出.这是真的吗?
现实生活中利用力的合成与分解求解的实例相当多,如斜拉索公路桥、用斧子劈木桩,另外,还有汽车换轮胎时用的剪式千斤顶、砖石结构的拱桥、工人向车上装货物时使用较长的木板、将立交桥的匝道建造得很长等。
课堂小结
THANKS
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
