冀教版八年级上册17.3 勾股定理(第一课时) 课件(共24张PPT)
文档属性
| 名称 | 冀教版八年级上册17.3 勾股定理(第一课时) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-03 08:13:34 | ||
图片预览



文档简介
(共24张PPT)
17.3 勾股定理(通用)
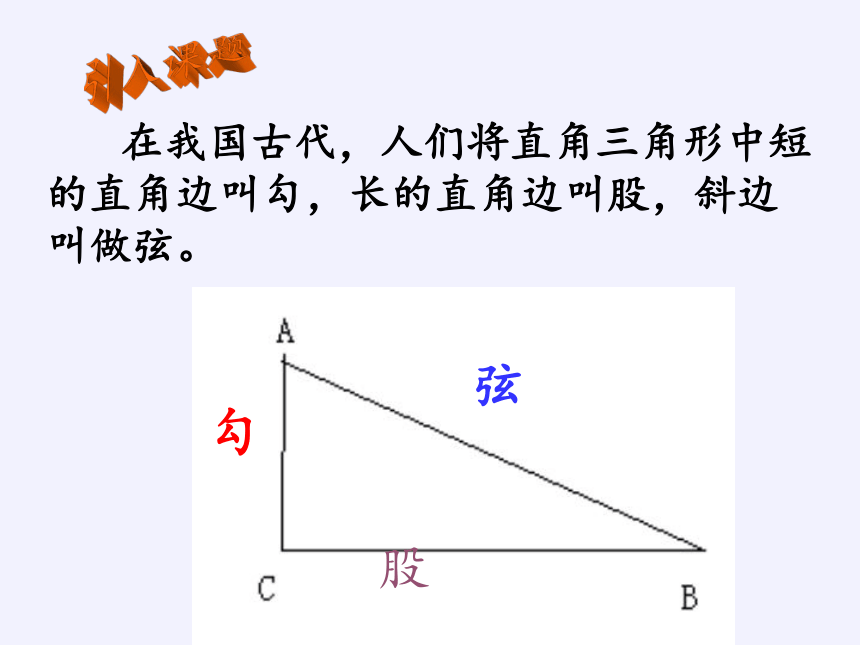
勾
股
弦
在我国古代,人们将直角三角形中短的直角边叫勾,长的直角边叫股,斜边叫做弦。
引入课题
你知道勾股定理吗?
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
这就是本届大会会徽的图案.
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们来观察右图中的地面,看看有什么发现?发现问题的孩子,给大家一起分享!
情景问题
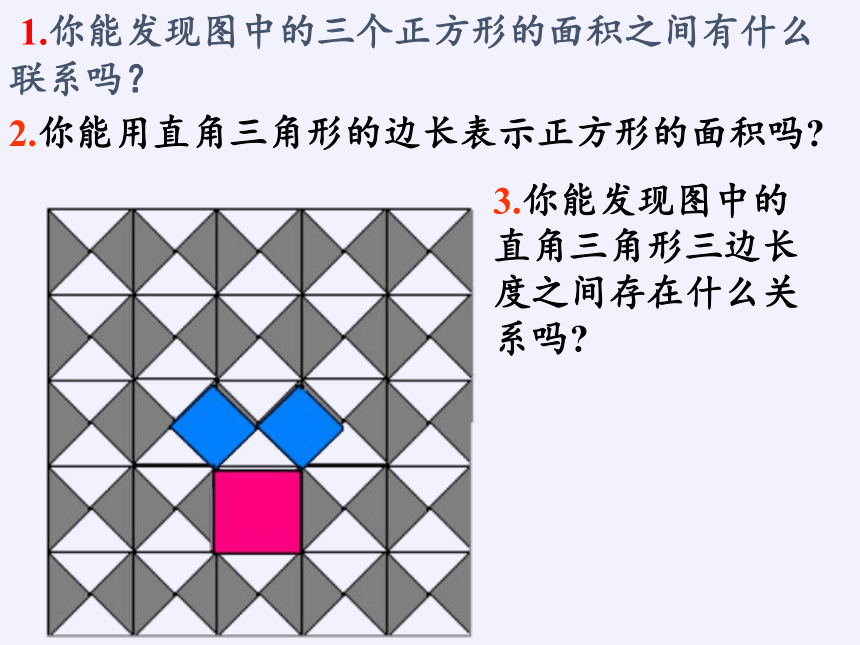
1.你能发现图中的三个正方形的面积之间有什么联系吗?
2.你能用直角三角形的边长表示正方形的面积吗
3.你能发现图中的直角三角形三边长度之间存在什么关系吗
探索勾股定理
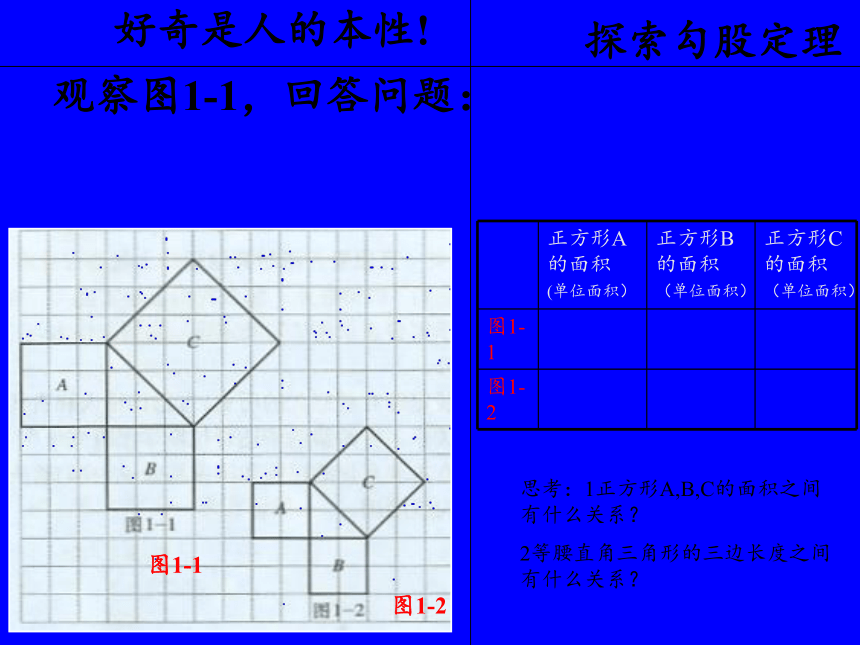
观察图1-1,回答问题:
图1-1
图1-2
好奇是人的本性!
正方形A的面积 (单位面积) 正方形B的面积 (单位面积) 正方形C的面积
(单位面积)
图1-1
图1-2
思考:1正方形A,B,C的面积之间有什么关系?
2等腰直角三角形的三边长度之间有什么关系?
探索勾股定理
观察图1-1,回答问题:
图1-1
图1-2
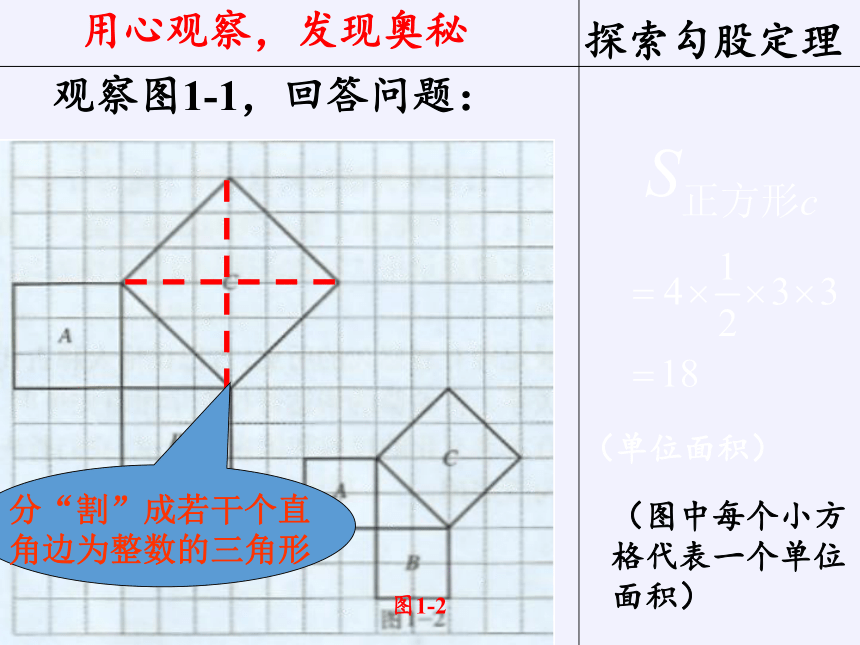
用心观察,发现奥秘
(图中每个小方格代表一个单位面积)
(单位面积)
分“割”成若干个直角边为整数的三角形
探索勾股定理
观察图1-1,回答问题:
图1-1
图1-2
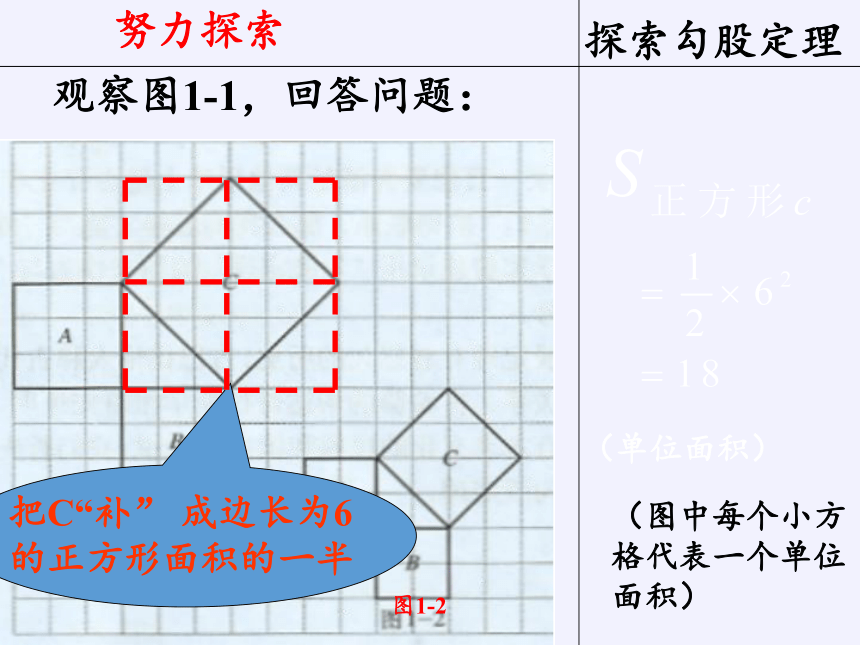
努力探索
(图中每个小方格代表一个单位面积)
(单位面积)
把C“补” 成边长为6的正方形面积的一半
探索勾股定理
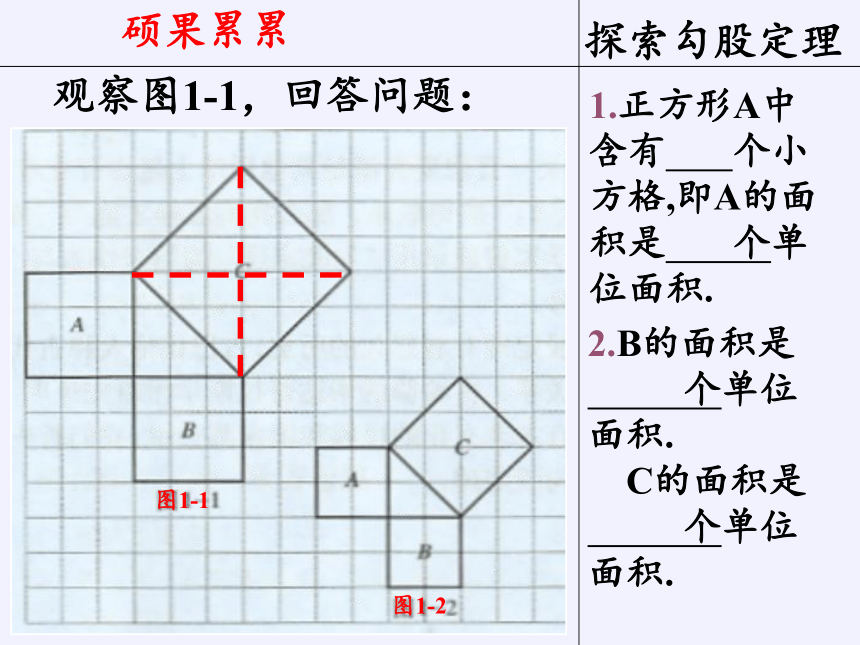
观察图1-1,回答问题:
1.正方形A中含有 个小方格,即A的面积是 个单位面积.
2.B的面积是
个单位面积.
C的面积是
个单位面积.
图1-1
图1-2
硕果累累
探索勾股定理
观察图1-2,回答问题:
1.正方形A中含有 个小方格,即A的面积是 个单位面积.
2.B的面积是
个单位面积. C的面积是
个单位面积.
图1-1
图1-2
飞向成功
4
4
4
8
数学家毕达哥拉斯的发现:
正方形A、B、C的面积有什么关系?
A
B
C
A的面积+ B的面积= C的面积
SA+SB=SC
直角三角形三边有
什么关系?写出关系式
B
C
a
b
c
A
设:等腰直角三角形的三边长分别是a、b、c
猜想:
两直角边a、b与斜边c 之间的关系?
A的面积+ B的面积= C的面积
a2+b2=c2
SA+SB=SC
对于等腰直角三角形有这样的性质:
那么对于一般的直角三角形是否也有这样的性质呢?
归纳小结:
两直角边的平方和等于斜边的平方
思考
A
B
C
图1-3
A
B
C
图1-4
3.三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
议一议
A
B
C
a
c
b
在一般直角三角形中,它的三边长之间有何关系?
想一想
A
B
C
a
c
b
SA+SB=SC
设:直角三角形的三边长分别是a、b、c
a2+b2=c2
两条直角边上的正方形面积之和等于斜边上的正方形的面积.
┏
a2+b2=c2
a
c
b
如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。
勾
股
弦
命题1:
c
b a
依据科学理论的证实:
我国汉代的数学家赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与4个直角三角形的面积和得:
直角三角形两直角边的平方和等于斜边的平方
a
b
你能用这个图试着证明勾股定理吗?
赵爽弦图
定理:经过证明被确认为正确的命题叫做定理。
勾股定理:
如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2
A
B
C
股b
勾 a
弦c
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )
A.3米 B.4米 C.5米 D.6米
C
3
4
1、直角 ABC的两直角边a=5,b=12,c=_____
2、直角 ABC的一条直角边a=10,斜边 c=26,则b= ( )。
3、已知:∠C=90°,a=6, a:b=3:4,求b和c。
当堂测试
c
a
b
限时8分钟
(1)蜘蛛急于想捉住苍蝇,沿着长方体的表面向上爬,它要从点A爬到点B处,有无数条路线,它们有长有短,蜘蛛究竟应该沿着怎样的路线爬上去,所走的路程会最短。你能帮蜘蛛找到最短路径吗?已知AC=4 cm CD=3cm BD=12cm
(2)若蜘蛛爬行的速度是每秒10cm,问蜘蛛沿长方体表面至少爬行几秒钟,才能迅速地抓到苍蝇?
A
C
D
B
G
F
H
学以致用
1、本节课我们经历了怎样的过程?
2、本节课我们学到了什么?谈谈与大家分享
学有所获
谢 谢
17.3 勾股定理(通用)
勾
股
弦
在我国古代,人们将直角三角形中短的直角边叫勾,长的直角边叫股,斜边叫做弦。
引入课题
你知道勾股定理吗?
这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.
这就是本届大会会徽的图案.
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
我们来观察右图中的地面,看看有什么发现?发现问题的孩子,给大家一起分享!
情景问题
1.你能发现图中的三个正方形的面积之间有什么联系吗?
2.你能用直角三角形的边长表示正方形的面积吗
3.你能发现图中的直角三角形三边长度之间存在什么关系吗
探索勾股定理
观察图1-1,回答问题:
图1-1
图1-2
好奇是人的本性!
正方形A的面积 (单位面积) 正方形B的面积 (单位面积) 正方形C的面积
(单位面积)
图1-1
图1-2
思考:1正方形A,B,C的面积之间有什么关系?
2等腰直角三角形的三边长度之间有什么关系?
探索勾股定理
观察图1-1,回答问题:
图1-1
图1-2
用心观察,发现奥秘
(图中每个小方格代表一个单位面积)
(单位面积)
分“割”成若干个直角边为整数的三角形
探索勾股定理
观察图1-1,回答问题:
图1-1
图1-2
努力探索
(图中每个小方格代表一个单位面积)
(单位面积)
把C“补” 成边长为6的正方形面积的一半
探索勾股定理
观察图1-1,回答问题:
1.正方形A中含有 个小方格,即A的面积是 个单位面积.
2.B的面积是
个单位面积.
C的面积是
个单位面积.
图1-1
图1-2
硕果累累
探索勾股定理
观察图1-2,回答问题:
1.正方形A中含有 个小方格,即A的面积是 个单位面积.
2.B的面积是
个单位面积. C的面积是
个单位面积.
图1-1
图1-2
飞向成功
4
4
4
8
数学家毕达哥拉斯的发现:
正方形A、B、C的面积有什么关系?
A
B
C
A的面积+ B的面积= C的面积
SA+SB=SC
直角三角形三边有
什么关系?写出关系式
B
C
a
b
c
A
设:等腰直角三角形的三边长分别是a、b、c
猜想:
两直角边a、b与斜边c 之间的关系?
A的面积+ B的面积= C的面积
a2+b2=c2
SA+SB=SC
对于等腰直角三角形有这样的性质:
那么对于一般的直角三角形是否也有这样的性质呢?
归纳小结:
两直角边的平方和等于斜边的平方
思考
A
B
C
图1-3
A
B
C
图1-4
3.三个正方形A,B,C面积之间有什么关系?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.
议一议
A
B
C
a
c
b
在一般直角三角形中,它的三边长之间有何关系?
想一想
A
B
C
a
c
b
SA+SB=SC
设:直角三角形的三边长分别是a、b、c
a2+b2=c2
两条直角边上的正方形面积之和等于斜边上的正方形的面积.
┏
a2+b2=c2
a
c
b
如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。
勾
股
弦
命题1:
c
b a
依据科学理论的证实:
我国汉代的数学家赵爽指出:四个全等的直角三角形如下拼成一个中空的正方形,由大正方形的面积等于小正方形的面积与4个直角三角形的面积和得:
直角三角形两直角边的平方和等于斜边的平方
a
b
你能用这个图试着证明勾股定理吗?
赵爽弦图
定理:经过证明被确认为正确的命题叫做定理。
勾股定理:
如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2
A
B
C
股b
勾 a
弦c
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )
A.3米 B.4米 C.5米 D.6米
C
3
4
1、直角 ABC的两直角边a=5,b=12,c=_____
2、直角 ABC的一条直角边a=10,斜边 c=26,则b= ( )。
3、已知:∠C=90°,a=6, a:b=3:4,求b和c。
当堂测试
c
a
b
限时8分钟
(1)蜘蛛急于想捉住苍蝇,沿着长方体的表面向上爬,它要从点A爬到点B处,有无数条路线,它们有长有短,蜘蛛究竟应该沿着怎样的路线爬上去,所走的路程会最短。你能帮蜘蛛找到最短路径吗?已知AC=4 cm CD=3cm BD=12cm
(2)若蜘蛛爬行的速度是每秒10cm,问蜘蛛沿长方体表面至少爬行几秒钟,才能迅速地抓到苍蝇?
A
C
D
B
G
F
H
学以致用
1、本节课我们经历了怎样的过程?
2、本节课我们学到了什么?谈谈与大家分享
学有所获
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
